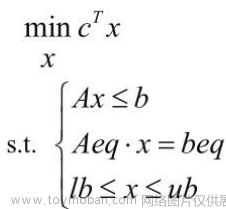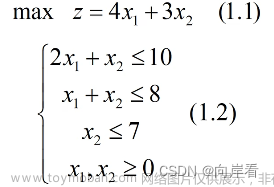线性规划模型（数学建模python版）-Toy模板网

这篇具有很好参考价值的文章主要介绍了线性规划模型（数学建模python版）。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

前言：本篇文章只涉及问题的应用层面（如何调用包调用函数，如何把问题归结为一般形式方便使用第三方库中的函数求解），不涉及问题的具体求解原理。

一、回顾以前我们学习到的线性规划

1.以前遇到的线性规划模型

首先回顾一下高中学过的线性规划：求一个线性目标函数在先行可行域内的最值问题。

高中遇到的问题：配送运输问题，生产规划问题、几何切割问题、买卖利润问题。

我们当时的做法无非分为算交点直接带入的激进派办法和老老实实地画图的保守派办法（）。

2.现在遇到的线性规划问题：

(1)多变量问题；

(2)目标盘函数不只是一次（非线性）

以上两种已经不能使用之前的办法做了

以下两种情况只是对执行域进行划分即可

(3)可行域中出现方程（易解决）

(4)变量也有自己的范围（易解决）

二、python对矩阵的操作以及线性规划的求解

学习这部分是为了对原始数据进行处理，以处理到可以使用python库中的函数可以解决的样子。

3.运用python进行矩阵运算：

下面是为了解决线性规划问题而需要掌握的一些矩阵运算的基本操作，主要是用到numpy库，不会的话可以运行一下下面的代码：

import numpy as np
a=np.array([[1,2,3],[4,5,6]])
b=np.array([[1,2],[3,4],[5,6]])
c=np.array([[1,2,3]])
d=np.array([[9,8,7],[3,2,1]])
#矩阵加法
print("矩阵加法:")
sum=a+d
print(sum)
#数乘
print("矩阵数乘：")
e=3*a
print(e)
#矩阵乘法
print("矩阵乘法：")
e=np.dot(a,b)
print(e)
#元素乘法
print("元素对应相乘：")
e=a*d
print(e)
#转置
print("转置：")
e=c.T
print(e)
#逆矩阵
f=np.array([[1,2],[3,4]])
res=np.linalg.inv(f)
print("矩阵求逆：")
print(res)
#行列式
print("行列式的值：")
res=np.linalg.det(f)
print(res)
#矩阵的秩
e=np.linalg.matrix_rank(d)
print("矩阵d的秩：")
print(e)

贴个结果：线性规划模型（数学建模python版）,数学建模

4.使用python对线性方程组进行求解

eg:

$线性规划模型（数学建模python版）,数学建模$

用lnumpy包有两个解法：

一个是运用线性代数中的逆矩阵：

一个是已经封装好的函数np.linalg.solve(A,b)

代码如下：

import numpy as np
A=np.array([[10,-1,-2],[-1,10,-2],[-1,-1,5]])
b=np.array([-72,83,42])
inv_A=np.linalg.inv(A)
x=inv_A.dot(b)
print(x)
x=np.linalg.solve(A,b)
print(x)

这里推荐用第二个，方便。

当然，会出现有的变量前的系数为0的情况，这需要我们自己补充0：

$线性规划模型（数学建模python版）,数学建模$

则对应的系数矩阵为：

5.python封装好的求解线性规划的函数：

线性规划的标准形式：

注意：一定要把任何形式的线性规化成上面的形式，这样才可以套用python的函数进行求解。

：我们把它叫做问题（要求解的目标）

我们把它叫做约束条件：

相信大家对这个应该比较熟悉，当然如果是第一次见，看看下面的这个例子也会明白是啥意思。

举个例子：若要求解下面的线性规划

$线性规划模型（数学建模python版）,数学建模$

可以看到，这个和我们要的标准形式还是有差别的，比如问题要求解的是最大值，并且不等号也不全是小于等于，这就需要我们加负号变化一下：

先看问题：我们要求的是z的最大值，换言之，我们可以先求-z的最小值，然后取相反数。

约束条件也是一样的，加负号来改变不等号方向。

最后的求解代码如下：

from scipy import optimize as op
import numpy as np
c=np.array([-2,-3,5])
A=np.array([[-2,5,-1],[1,3,1]])
b=np.array([-10,12])
Aeq=np.array([[1,1,1]])
beq=np.array([7])
x1=(0,None)
x2=(0,None)
x3=(0,None)
ans=op.linprog(c,A,b,Aeq,beq,bounds=(x1,x2,x3))
print(ans)

运行结果如下：有很多信息，比如算了多少轮（nit），精度等等，不同的版本跑出来可能不太一样。我们要注意的只是答案就好（画红线部分）：

线性规划模型（数学建模python版）,数学建模