力扣236——二叉树的最近公共祖先-Toy模板网

这篇具有很好参考价值的文章主要介绍了力扣236——二叉树的最近公共祖先。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

祝大家新年快乐呀，虽这段时间正值过年，但是我们不要忘记停下学习的脚步。今天我们一起看一到力扣上的经典二叉树OJ题，求二叉树两个结点最近的公共祖先。

https://leetcode.cn/problems/lowest-common-ancestor-of-a-binary-tree/description/

链接给大家放在这里啦，大家一点即达

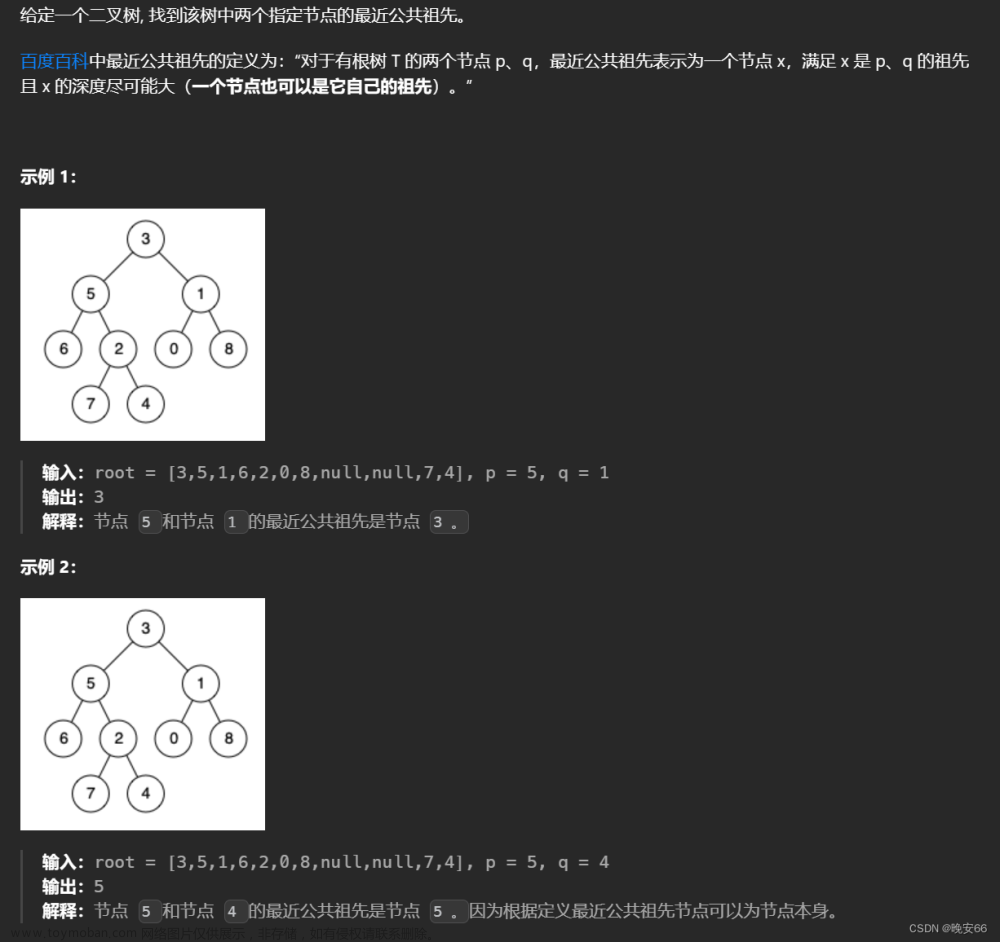
力扣236——二叉树的最近公共祖先,leetcode,算法首先我们看到题目，这道题并没有告诉我们这是一棵怎么样的二叉树，不是完全二叉，也不是搜索二叉，所以这道题做起来就比较棘手，完全二叉树的话我们可以根据结点的编号查找，搜索二叉我们也可以按照大小确定范围，但是眼前这颗数完全是一个乱序的，所以这道题怎么下手呢？

方法一

我们不妨先确定要查找的两个结点在根结点的哪边，我们拿5和8举例子

力扣236——二叉树的最近公共祖先,leetcode,算法很明显。这两个结点一个在根结点的左边，一个在右边，所以他们最近公共结点肯定就是根节点。

那如果在同一边呢？比如6和4，

力扣236——二叉树的最近公共祖先,leetcode,算法结点6和4都在根节点的左子树上，我们可以用刚才的方法，递归根节点的左子树，以结点5为跟，就可以求出他们最近的公共结点为5；思路有了，现在我们编写代码

我们先封装一个函数判断结点是否在这个以root为根结点的二叉树内：

bool IsTree(TreeNode*root,TreeNode* x)
    {
        if(root==nullptr)
        {
            return false;
        }
        return root==x||IsTree(root->left,x)||IsTree(root->right,x);
    }

然后我们在给定的函数内实现出这个函数。

这里教大家一个简便的方法。我们定义几个bool变量：

bool Leftp,Rightp,Leftq,Rightq;//依次代表的含义是p在左子树，P在右子树，q在左子树，q在右子树

然后我们去找p在root的那一边，把返回值给Leftp,让Rightp=!Left;

Leftp=IsTree(root->left,p);
Rightp=!Leftp;

这样写大家能理解什么意思吗？在root的左子树去找结点p的结果赋给Leftp,不管是不是在左边，右边的结果肯定就是！Leftp,假如Leftp是true，那Rightp就是false;如果Leftp是false,那Rightp就是true;二者肯定一真一假，判断q结点在哪边也是如此

Leftq=IsTree(root->left,q);
Rightq=!Leftq;

然后我们判断如果两个结点pq有一个是根节点root的话，那就返回root就可以了

if(p==root||q==root)
        {
            return root;
        }

其次，判断，如果pq一个在根节点左边，一个在右边，那还是返回根节点。即

if((Leftp&&Rightq)||(Rightp&&Leftq))//中间用||连接是因为我们也不知道他们在哪边，反正肯定有一组是真的
{
    return root;
}

然后再判断他们在同一边的情况,代码运行到这里，肯定能证明他们不在同一边，我们先判断同时在左子树的情况：

        else if(Leftp&&Leftq)
        {
            return lowestCommonAncestor(root->left,p,q);
        }

剩下的就是同时在右子树的情况：

else{
        return lowestCommonAncestor(root->right,p,q);
    }

然后我们提交，就可以看到通过啦。但是我们思考一下，这样的写法时间复杂度是很大的。如果这棵树是一个类似于单边的二叉树，也就是另外一边的结点个数很少很少，几乎全部集中在一边，且要找的两个结点都在最后，即：

力扣236——二叉树的最近公共祖先,leetcode,算法

我们要查找的两个结点在这个位置，它的时间复杂度是多少？可以看到，我们以3为根结点查询1和3在哪边需要走N-2次+N-3次，然后递归以10为根节点查找，再递归以8为根节点查找.......时间复杂度其实是O(N^2)的。

bool IsTree(TreeNode*root,TreeNode* x)
    {
        if(root==nullptr)
        {
            return false;
        }
        return root==x||IsTree(root->left,x)||IsTree(root->right,x);
    }
    TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
        bool Leftp,Rightp,Leftq,Rightq;
        Leftp=IsTree(root->left,p);
        Rightp=!Leftp;
        Leftq=IsTree(root->left,q);
        Rightq=!Leftq;
        if(p==root||q==root)
        {
            return root;
        }
        if((Leftp&&Rightq)||(Rightp&&Leftq))
        {
            return root;
        }
        else if(Leftp&&Leftq)
        {
            return lowestCommonAncestor(root->left,p,q);
        }
        else{
            return lowestCommonAncestor(root->right,p,q);
        }
}

方法二

下面我们介绍第二种方法

第二种方式是我们记录两个结点的路径，即从根结点到找到他们之间所有的结点。例如：

力扣236——二叉树的最近公共祖先,leetcode,算法

结点6的路径是3->5->6,结点4的路径是3->5->2->4,把他们都放在两个栈里面，比较栈的特点是后进先出，然后比较这个两个栈的第一个相同的栈顶元素。这样的话我们最坏无非就是遍历2次这棵树就可以，定义两个栈，算是以空间换时间。下面我们开始实现

我们首先需要在原函数定义两个栈，一个用于存放p结点的路径，一个存放q结点的路径

TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
stack<TreeNode*> ppath;
stack<TreeNode*>qpath;
}

然后我们需要封装一个函数用来求结点走过的路径Getpath();参数需要根节点，待求结点,栈，即

bool Getpath(TreeNode* root, TreeNode* x, stack<TreeNode*>& path)//传引用是为了我们在调用这个函数时对这个栈的修改可以随时生效，不需要再拷贝

用bool类型是为了我们找到这个结点时就直接返回不再往下走。

下面我们实现这个函数，首先判断根节点为空，那就返回false，接下来先把根节点入栈，然后判断根结点是要求的路径的结点，是的话返回true；

bool Getpath(TreeNode* root, TreeNode* x, stack<TreeNode*>& path)
{
	if (root == nullptr)
	{
		return false;
	}
	path.push(root);
	if (root == x)
	{
		return true;
	}
}

代码走到这里，那就证明根结点不是x，我们递归左子树，如果左子树为真，返回true;左子树遇到空结点返回false,下来递归右子树，右子树也是如此；

if (Getpath(root->left, x, path))
		return true;
	
	if (Getpath(root->right, x, path))
		return true;

代码走到这里，证明根节点及它的左右孩子结点都不是x，我们需要把这个根节点出栈的，比如：

力扣236——二叉树的最近公共祖先,leetcode,算法

比如我们求结点4的路径，代码运行到查找5的左孩子时，6先进栈，然后递归6的左右子树，都为空，已经把6的左右子树都查找完毕，所以4的路径不经过结点6，那这个时候需要让6出栈，然后返回false,返回上一层递归。

if (root != x)
	{
		path.pop();
	}
	return false;

这个函数就封装完成。

下面写原函数，原函数我们首先要定义两个栈，上面已经定义过，这个是我们先走一遍p的路径，再走一遍q的路径，这个时候ppath和qpath两个栈里面存放着p和q的路径，我们需要让这两个栈的大小相等，因为从根节点到最近公共祖先肯定是完全一样的，这样才能找出公共路径。

while (ppath.size() != qpath.size())
{
	if (ppath.size() > qpath.size())
		ppath.pop();
	else
		qpath.pop();
}

这个时候两栈存放的数据个数相等，只需比较栈顶元素是否相等，不相等再同时出栈，相等时返回栈顶元素就可以啦。

while (ppath.top() != qpath.top())
{
	ppath.pop();
	qpath.pop();
}
return ppath.top();

这样代码就能提交过啦。时间复杂度也很乐观。文章来源地址https://www.toymoban.com/news/detail-829764.html

bool Getpath(TreeNode* root, TreeNode* x, stack<TreeNode*>& path)
{
	if (root == nullptr)
	{
		return false;
	}
	path.push(root);
	if (root == x)
	{
		return true;
	}
	if (Getpath(root->left, x, path))
		return true;;
	
	if (Getpath(root->right, x, path))
		return true;
	if (root != x)
	{
		path.pop();
	}
	return false;
}
TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
    stack<TreeNode*> ppath;
stack<TreeNode*>qpath;
Getpath(root, p, ppath);
Getpath(root, q, qpath);
while (ppath.size() != qpath.size())
{
	if (ppath.size() > qpath.size())
		ppath.pop();
	else
		qpath.pop();
}
while (ppath.top() != qpath.top())
{
	ppath.pop();
	qpath.pop();
}
return ppath.top();
    }

到了这里，关于力扣236——二叉树的最近公共祖先的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！