有意向获取代码,请转文末观看代码获取方式~也可转原文链接获取~

1 基本定义
PSO-BP神经网络回归预测(多输入多输出)算法是一种结合粒子群优化算法(PSO)和反向传播(BP)神经网络的混合算法。该算法的原理如下:
-
数据预处理:在进行PSO-BP神经网络回归预测之前,需要对数据进行预处理,包括数据清洗、特征选择和数据归一化等步骤。
-
初始化神经网络:首先需要初始化神经网络的结构和初始权值。神经网络可以包含多个隐层和一个输出层,每个层都包含多个神经元。在初始化时,需要确定每个层的神经元数量,并为每个权值和阈值赋予一个随机初始值。
-
粒子群初始化:在PSO-BP中,每个粒子都代表一个神经网络的权值和阈值组合。需要初始化一定数量的粒子,并为每个粒子随机生成初始速度和位置。
-
PSO迭代:PSO迭代是整个算法的核心部分。迭代过程中,每个粒子都会根据当前速度和位置进行更新,并根据适应度函数评估自身的性能。
-
更新粒子速度和位置:在更新粒子速度和位置时,需要考虑三个因素:惯性因子、个体历史最优解和群体历史最优解。具体的更新公式如下:v_new=w_v_old+c1_r1*(pbest-position)+c2_r2_(gbest-position)position_new=position+v_new其中,w是惯性因子,c1和c2是学习因子,r1和r2是随机数,pbest是粒子的个体历史最优解,gbest是群体历史最优解。
-
更新粒子个体最优解和全局最优解:在每次迭代中,需要更新粒子的个体历史最优解和全局最优解。如果当前粒子的适应度比个体历史最优解更好,则更新个体历史最优解。如果所有粒子中的适应度都比全局历史最优解更好,则更新全局历史最优解。
-
更新权值和阈值:根据个体历史最优解和全局历史最优解来更新神经网络的权值和阈值。具体的更新公式如下:weight_new=weight_old+learning_rate*(pbest_position-weight_old)+learning_rate*(gbest_position-weight_old)其中,learning_rate是学习率,pbest_position和gbest_position分别是个体历史最优解和全局历史最优解的位置。
-
判断终止条件:当满足一定的终止条件时,算法停止迭代。常见的终止条件包括达到最大迭代次数、粒子的适应度达到预设阈值等。
通过以上步骤,PSO-BP神经网络回归预测(多输入多输出)算法能够根据输入的特征值预测出相应的输出值,并利用PSO算法优化神经网络的初始权值和阈值,提高预测精度。
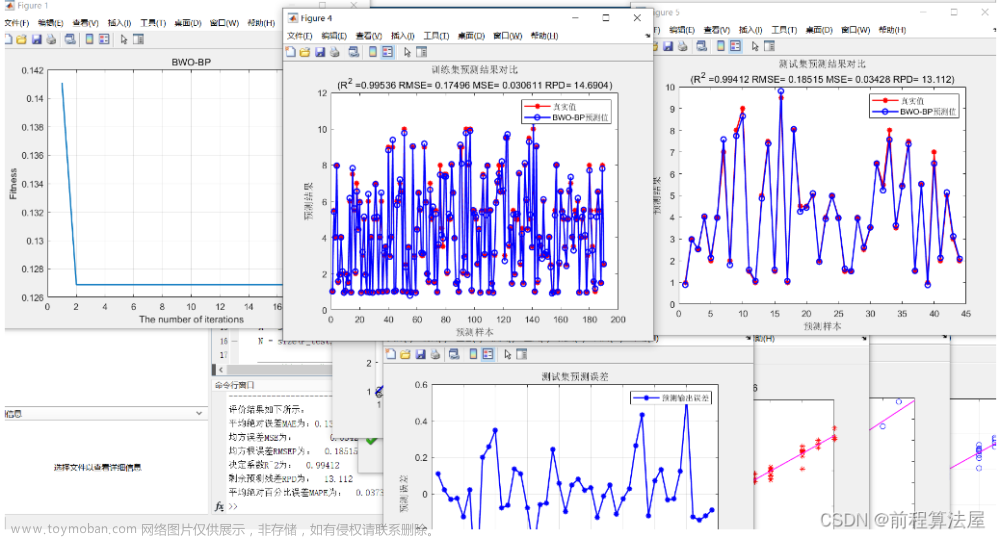
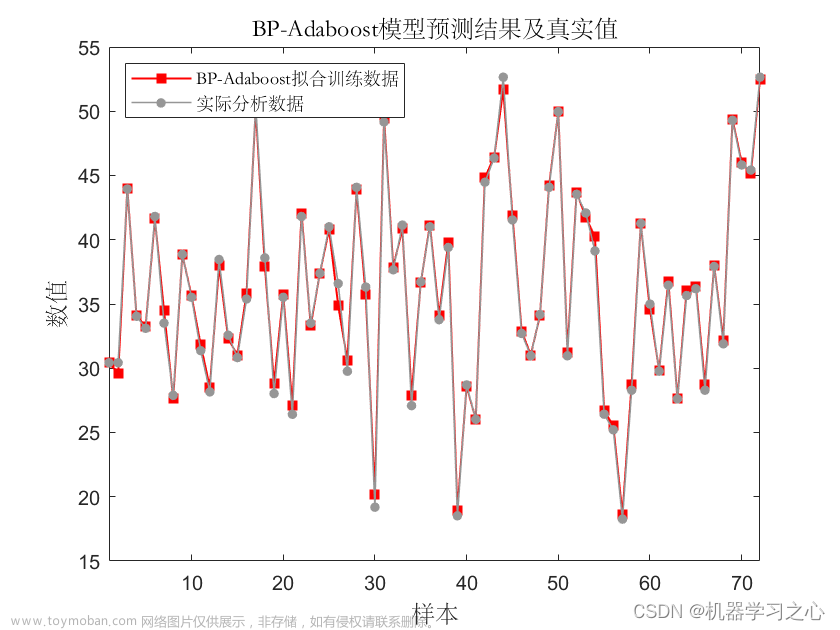
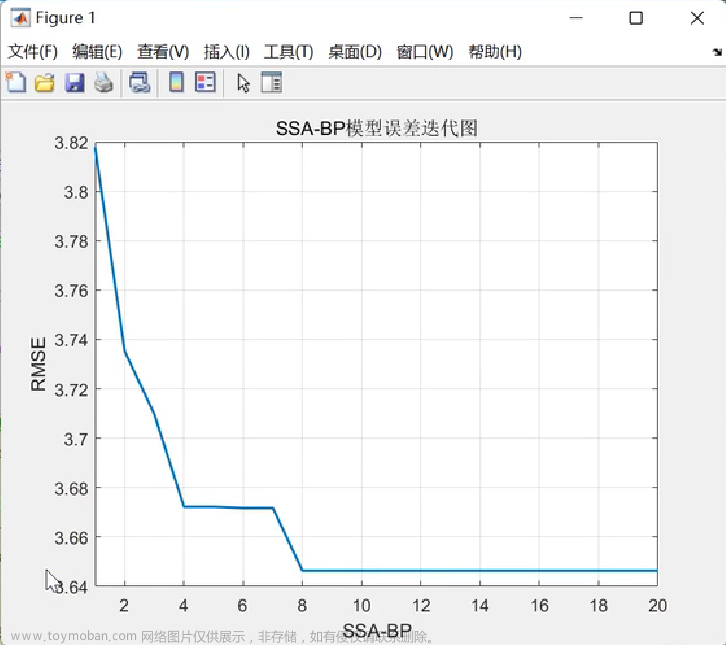
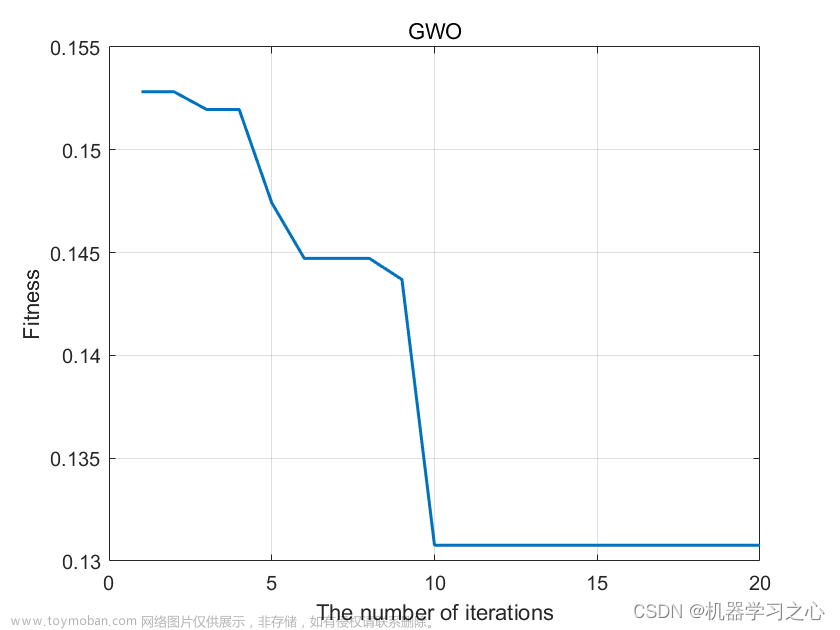
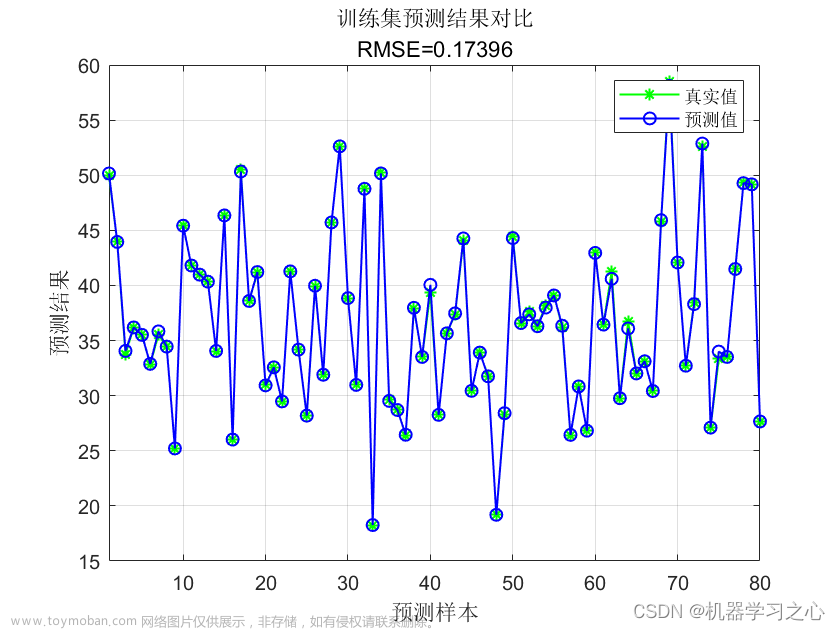
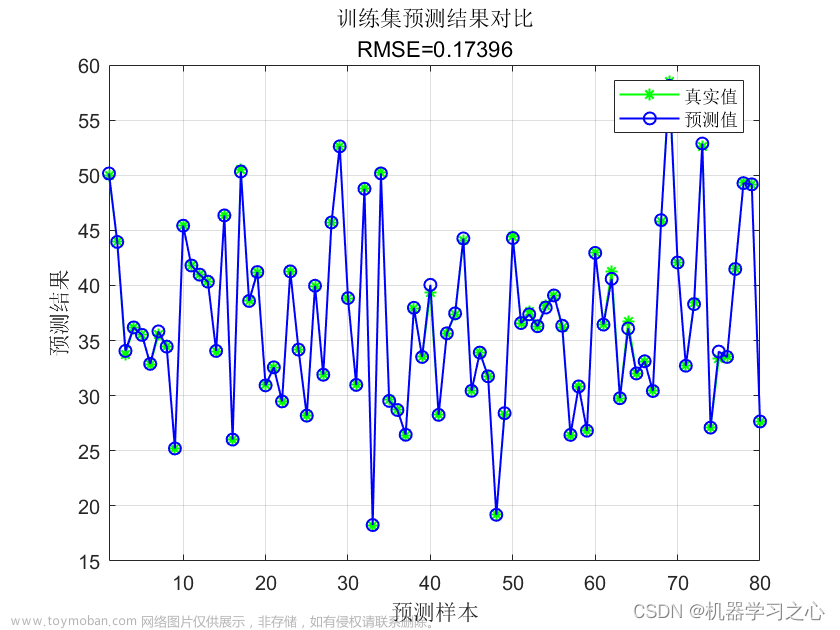
2 出图效果
附出图效果如下:





附视频教程操作:文章来源:https://www.toymoban.com/news/detail-829857.html
【MATLAB】PSO文章来源地址https://www.toymoban.com/news/detail-829857.html
到了这里,关于【MATLAB】PSO_BP神经网络回归预测(多输入多输出)算法原理的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!