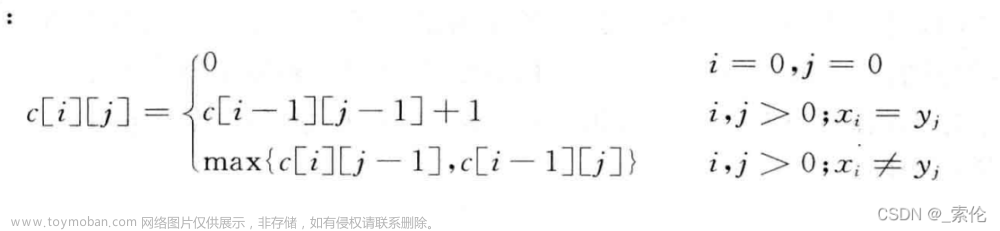【动态规划】最长公共子序列Python实现

个人主页：丷从心

系列专栏：动态规划算法

问题描述

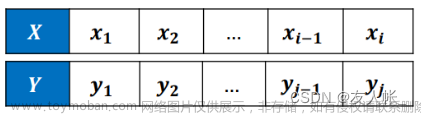
• 给定两个序列 X = {   x 1 , x 2 , ⋯   , x m   } X = \set{x_{1} , x_{2} , \cdots , x_{m}} X={x1​,x2​,⋯,xm​}和 Y = {   y 1 , y 2 , ⋯   , y n   } Y = \set{y_{1} , y_{2} , \cdots , y_{n}} Y={y1​,y2​,⋯,yn​}，找出$X$和$Y$的最长公共子序列

最长公共子序列的结构

• 设序列 X = {   x 1 , x 2 , ⋯   , x m   } X = \set{x_{1} , x_{2} , \cdots , x_{m}} X={x1​,x2​,⋯,xm​}和 Y = {   y 1 , y 2 , ⋯   , y n   } Y = \set{y_{1} , y_{2} , \cdots , y_{n}} Y={y1​,y2​,⋯,yn​}的最长公共子序列为 Z = {   z 1 , z 2 , ⋯   , z k   } Z = \set{z_{1} , z_{2} , \cdots , z_{k}} Z={z1​,z2​,⋯,zk​}
  • 若$x_m=y_n$，则$z_k=x_m=y_n$，且$Z_{k-1}$是$X_{m-1}$和$Y_{n-1}$的最长公共子序列
  • 若$x_m\ne y_n$且$z_k\ne x_m$，则$Z$是$X_{m-1}$和$Y$的最长公共子序列
  • 若$x_m\ne y_n$且$z_k\ne y_n$，则$Z$是$X$和$Y_{n-1}$的最长公共子序列

子问题的递归结构

• 当$x_m=y_n$时，找出$X_{m-1}$和$Y_{n-1}$的最长公共子序列，然后在其尾部加上$x_m$
• 当$x_m\ne y_n$时，找出$X_{m-1}$和$Y$的一个最长公共子序列及$X$和$Y_{n-1}$的一个最长公共子序列，这两个公共子序列中较长者即为$X$和$Y$的最长公共子序列

$c[i][j]$递归方程

c [ i ] [ j ] = { 0 , i = 0 或 j = 0 c [ i − 1 ] [ j − 1 ] + 1 , i , j > 0 ; x i = y j max ⁡ {   c [ i ] [ j − 1 ] , c [ i − 1 ] [ j ]   } , i , j > 0 ; x i ≠ y j c[i][j] = \begin{cases} 0 , & i = 0 或 j = 0 \\ c[i - 1][j - 1] + 1 , & i , j > 0 ; x_{i} = y_{j} \\ \max\set{c[i][j - 1] , c[i - 1][j]} , & i , j > 0 ; x_{i} \neq y_{j} \end{cases} c[i][j]=⎩ ⎨ ⎧​0,c[i−1][j−1]+1,max{c[i][j−1],c[i−1][j]},​i=0或j=0i,j>0;xi​=yj​i,j>0;xi​=yj​​文章来源地址https://www.toymoban.com/news/detail-829929.html

时间复杂性

• 由于每个数组单元的计算耗费$O(1)$时间，因此算法耗时$O(mn)$

构造最长公共子序列

• 在算法$LCS$中，每次递归调用使$i$或$j$减$1$，因此算法的计算时间为$O(m+n)$

Python实现

def longest_common_subsequence(str_1, str_2):
    m = len(str_1)
    n = len(str_2)

    # 创建一个二维数组来存储子问题的解
    dp = [[0] * (n + 1) for _ in range(m + 1)]

    # 填充二维数组
    for i in range(1, m + 1):
        for j in range(1, n + 1):
            if str_1[i - 1] == str_2[j - 1]:
                dp[i][j] = dp[i - 1][j - 1] + 1
            else:
                dp[i][j] = max(dp[i - 1][j], dp[i][j - 1])

    # 构造最长公共子序列
    lcs = ''

    i, j = m, n
    while i > 0 and j > 0:
        if str_1[i - 1] == str_2[j - 1]:
            lcs = str_1[i - 1] + lcs

            i -= 1
            j -= 1
        elif dp[i - 1][j] > dp[i][j - 1]:
            i -= 1
        else:
            j -= 1

    return lcs


str_1 = 'ABCDGH'
str_2 = 'AEDFHR'

lcs = longest_common_subsequence(str_1, str_2)

print(f'最长公共子序列: {lcs}')

最长公共子序列: ADH

算法的改进

• 如果只需要计算最长公共子序列的长度，则只用到数组$c$的第$i$行和第$i-1$行
• 因此，用两行的数组空间就可以计算出最长公共子序列的长度，可将空间需求减至 O ( min ⁡ {   m , n   } ) O(\min\set{m , n}) O(min{m,n})

到了这里，关于【动态规划】最长公共子序列Python实现的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！