图论之dfs与bfs的练习-Toy模板网

这篇具有很好参考价值的文章主要介绍了图论之dfs与bfs的练习。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

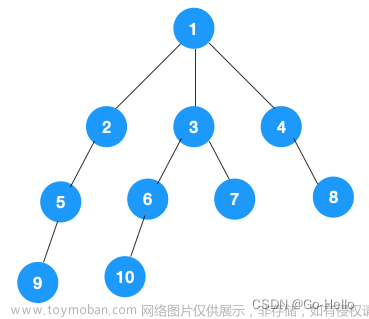
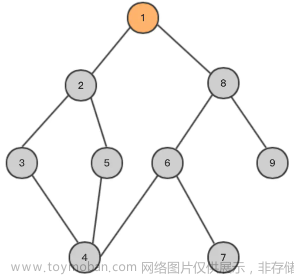
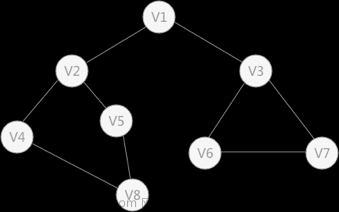
dfs--深度优选搜索

bfs--广度优先搜索

迷宫问题--dfs

问题：

给定一个n*m的二维迷宫数组其中S是起点，T是终点，*是墙壁（无法通过）， .是道路
问从起点S出发沿着上下左右四个方向走，能否走到T点？能输出"YES",否则输出"NO"。

8 8

*****...
*.S...**
*****.**
*****..*
*T..**.*
.**.**.*
..*....*
...*****

#include<iostream>
using namespace std;
const int N = 1e4 + 10;
char g[N][N];//迷宫数组
bool vis[N][N];//二维标记数组
//方向数组
int dx[] = { 0,0,-1,1 };
int dy[] = { 1,-1,0,0 };
int n, m;
int sx, sy, tx, ty;
bool flag;
void dfs(int px, int py) {
	//如果当前搜的点p是终点点t，终止搜索
	if (px == tx && py == ty) {
		flag = true;
		return;
	}
	//沿着点p的邻接点继续搜索
	for (int i = 0; i < 4; i++) {
		int bx=px+dx[i], by=py+dy[i];//生成邻接点
		if (bx<1 || bx>n || by<1 || by>m) continue;//迷宫图的边界
		if (g[bx][by] == '*') continue;//墙壁
		if (vis[bx][by]) continue;//走过的不再走
		vis[bx][by] = 1;
		dfs(bx, by);
	
	}
}
int main() {
	cin >> n >> m;
	for (int i = 1; i <= n; i++) {
		for (int j = 1; j <= m; j++) {
			cin >> g[i][j];
			if (g[i][j] == 'S') sx = i, sy = j;//找到起点的坐标
			if (g[i][j] == 'T') tx = i, ty = j;//找到终点的坐标
		}
	}
	vis[sx][sy] = 1;
	flag = false;
	dfs(sx, sy);
	if (flag) cout << "YES" << endl;
	else cout << "NO" << endl;
	return 0;
}

求迷宫问题的最短路--bfs

问题：

给定一个n*m的二维迷宫数组其中S是起点，T是终点，*是墙壁（无法通过）， .是道路
问从起点S出发沿着上下左右四个方向走，能否走到T点？如果能打印最短路径长度，否则输出0。

8 8

*****...
*.S...**
*****.**
*****..*
*T..**.*
.**.**.*
..*....*
...*****

#include<iostream>
#include<queue>
using namespace std;
const int N = 1e4 + 10;
char g[N][N];//迷宫数组
bool vis[N][N];//二维标记数组
//方向数组
int dx[] = { 0,0,-1,1 };
int dy[] = { 1,-1,0,0 };
int n, m;
int sx, sy, tx, ty;
struct point {
	int x, y, depth;
};
void bfs(point s) {
	queue<point> q;
	q.push(s);   vis[s.x][s.y] = 1;

	while (!q.empty()) {
		point cur = q.front();  q.pop();
		if (cur.x == tx && cur.y == ty) {
			flag = true;
			cout << cur.depth - 1 << endl;
			return;
		}
		//通过方向数组找到cur的邻接点，沿着邻接点继续广搜
		for (int i = 0; i < 4; i++) {
			int bx = cur.x + dx[i], by = cur.y + dy[i];//生成邻接点
			if (bx<1 || bx>n || by<1 || by>m) continue;
			if (g[bx][by] == '*') continue;
			if (vis[bx][by]) continue;
			vis[bx][by] = 1;
			q.push({ bx,by,cur.depth + 1 });
		}
	}
}
int main() {
	cin >> n >> m;
	for (int i = 1; i <= n; i++) {
		for (int j = 1; j <= m; j++) {
			cin >> g[i][j];
			if (g[i][j] == 'S') sx = i, sy = j;
			if (g[i][j] == 'T') tx = i, ty = j;
		}
	}
	vis[sx][sy] = 1;
	flag = false;
	bfs({ sx, sy ,1});
	return 0;
}

1215：迷宫

信息学奥赛一本通（C++版）在线评测系统

【题目描述】

一天Extense在森林里探险的时候不小心走入了一个迷宫，迷宫可以看成是由n×n�×�的格点组成，每个格点只有22种状态，.和#，前者表示可以通行后者表示不能通行。同时当Extense处在某个格点时，他只能移动到东南西北(或者说上下左右)四个方向之一的相邻格点上，Extense想要从点A走到点B，问在不走出迷宫的情况下能不能办到。如果起点或者终点有一个不能通行(为#)，则看成无法办到。

【输入】

第1行是测试数据的组数k�，后面跟着k�组输入。每组测试数据的第11行是一个正整数n(1≤n≤100)�(1≤�≤100)，表示迷宫的规模是n×n�×�的。接下来是一个n×n�×�的矩阵，矩阵中的元素为.或者#。再接下来一行是44个整数ha,la,hb,lbℎ�,��,ℎ�,��，描述A处在第haℎ�行, 第la��列，B处在第hbℎ�行, 第lb��列。注意到ha,la,hb,lbℎ�,��,ℎ�,��全部是从00开始计数的。

【输出】

k�行，每行输出对应一个输入。能办到则输出“YES”，否则输出“NO”。

【输入样例】
2
3
.##
..#
#..
0 0 2 2
5
.....
###.#
..#..
###..
...#.
0 0 4 0
【输出样例】
YES
NO

解法一：dfs

#include<iostream>
using namespace std;
const int N = 1e2 + 10;
char g[N][N];//迷宫数组
bool vis[N][N];//标记数组
int t,n, sx, sy, tx, ty;
//方向数组
int dx[] = { 0,0,1,-1 };
int dy[] = { 1,-1,0,0 };
bool flag;
void dfs(int px, int py) {
	if (px == tx && py == ty) {
		flag = true;
		return;
	}
	//沿着邻接点继续搜索
	for (int i = 0; i < 4; i++) {
		int bx = px + dx[i], by = py + dy[i];
		if (bx<1 || bx>n || by<1 || by>n) continue;
		if (g[bx][by] == '#') continue;
		if (vis[bx][by]) continue;
		//如果以上情况均不成立，证明邻接点有效，沿着该邻接点继续深搜
		vis[bx][by] = 1;//不标记会报栈溢出错误
		dfs(bx, by);
	}
}
int main() {
	cin >> t;
	while (t--) {
		cin >> n;
		for (int i = 1; i <= n; i++)
			for (int j = 1; j <= n; j++)
				cin >> g[i][j];  
		cin >> sx >> sy >> tx >> ty;
		sx++, sy++, tx++, ty++;//注意:本题下标从0开始
		//多组数据要将相关状态重置
		flag = false;
		memset(vis, 0, sizeof vis);//将vis数组全体清0
		vis[sx][sy] = 1;
		dfs(sx, sy);
		if (flag) cout << "YES" << endl;
		else cout << "NO" << endl;
	}
	return 0;
}

解法二：bfs

#include<iostream>
#include<queue>
using namespace std;
const int N = 1e2 + 10;
char g[N][N];//迷宫数组
bool vis[N][N];//标记数组
int t, n, sx, sy, tx, ty;
//方向数组
int dx[] = { 0,0,1,-1 };
int dy[] = { 1,-1,0,0 };
bool flag;
struct point {
	int x, y;
};
void bfs(point p) {
	queue<point> q;
	q.push(p);  vis[p.x][p.y] = 1;

	while (!q.empty()) {
		point cur=q.front();  q.pop();
		if (cur.x == tx && cur.y== ty) {
			flag = true;
			return;
		}
		//沿着邻接点继续搜索
		for (int i = 0; i < 4; i++) {
			int bx = cur.x + dx[i], by = cur.y + dy[i];
			if (bx<1 || bx>n || by<1 || by>n) continue;
			if (g[bx][by] == '#') continue;
			if (vis[bx][by]) continue;
			//如果以上情况均不成立，证明邻接点有效，沿着该邻接点继续深搜
			vis[bx][by] = 1;
			q.push({ bx,by });
		}
	}
}
int main() {
	cin >> t;
	while (t--) {
		cin >> n;
		for (int i = 1; i <= n; i++)
			for (int j = 1; j <= n; j++)
				cin >> g[i][j];   /*scanf(" %c", &g[i][j]); */
		cin >> sx >> sy >> tx >> ty;
		sx++, sy++, tx++, ty++;//注意本题下标从0开始
		//多组数据要将相关状态重置
		flag = false;
		memset(vis, 0, sizeof vis);//将vis数组全体清0
		vis[sx][sy] = 1;
		bfs({sx, sy});
		if (flag) cout << "YES" << endl;
		else cout << "NO" << endl;
	}
	return 0;
}

1216：红与黑

【题目描述】

有一间长方形的房子，地上铺了红色、黑色两种颜色的正方形瓷砖。你站在其中一块黑色的瓷砖上，只能向相邻的黑色瓷砖移动。请写一个程序，计算你总共能够到达多少块黑色的瓷砖。

【输入】

包括多组数据。每组数据的第一行是两个整数W和H，分别表示x方向和y方向瓷砖的数量。W和H都不超过20。在接下来的H行中，每行包括W个字符。每个字符表示一块瓷砖的颜色，规则如下:

1）‘.’：黑色的瓷砖；

2）‘#’：红色的瓷砖；

3）‘@’：黑色的瓷砖，并且你站在这块瓷砖上。该字符在每组数据中唯一出现一次。

当在一行中读入的是两个零时，表示输入结束。

【输出】

对每组数据，分别输出一行，显示你从初始位置出发能到达的瓷砖数(记数时包括初始位置的瓷砖)。

【输入样例】
6 9 
....#.
.....#
......
......
......
......
......
#@...#
.#..#.
0 0
【输出样例】
45

解法一：dfs

#include<iostream>
using namespace std;
const int N = 1e2 + 10;
char g[N][N];//迷宫数组
bool vis[N][N];//二维标记数组
//方向数组
int dx[] = { 0,0,-1,1 };
int dy[] = { 1,-1,0,0 };
int sx, sy;
int w, h;
int cnt;
void dfs(int px,int py)
{
	//沿着邻接点搜索
	for (int i = 0; i < 4; i++)
	{
		int bx = px + dx[i], by = py + dy[i];
		if (g[bx][by] == '#')continue;
		if (bx<1 || bx>w || by<1 || by>h)continue;
		if (vis[bx][by])continue;
		vis[bx][by] = 1;
		cnt++;
		dfs(bx, by);
	}
}

int main()
{
	/*注意：本题是先输入列再输入行*/
	while (cin >> h >> w && w && h)//注意要判断w和h都为0结束
	{
		for (int i = 1; i <= w; i++)
		{
			for (int j = 1; j <= h; j++)
			{
				cin >> g[i][j];
				if (g[i][j] == '@')
					sx = i, sy = j;
			}

		}
		//多组数据注意相关状态
		cnt = 1;
		memset(vis, 0, sizeof vis);//vis数组全体清0
		vis[sx][sy] = 1;
		dfs(sx, sy);
		cout << cnt << endl;
	}
	
	return 0;
}

解法二：bfs

#include<iostream>
#include<queue>
using namespace std;
const int N = 1e2 + 10;
char g[N][N];//迷宫数组
bool vis[N][N];//二维标记数组
//方向数组
int dx[] = { 0,0,-1,1 };
int dy[] = { 1,-1,0,0 };
int sx, sy;
int w, h;
int cnt;
struct point
{
	int x, y;
};
void dfs(point s)
{
	queue<point>q;
	q.push(s); vis[s.x][s.y] = 1;
	while (!q.empty()) 
	{
		point cur = q.front(); q.pop();
		//沿着邻接点搜索
		for (int i = 0; i < 4; i++)
		{
			int bx = cur.x + dx[i], by = cur.y + dy[i];
			if (g[bx][by] == '#')continue;
			if (bx<1 || bx>w || by<1 || by>h)continue;
			if (vis[bx][by])continue;
			vis[bx][by] = 1;
			cnt++;
			q.push({bx,by});
		}
	}
}

int main()
{
	/*注意：本题是先输入列再输入行*/
	while (cin >> h >> w && w && h)//注意要判断w和h都为0结束
	{
		for (int i = 1; i <= w; i++)
		{
			for (int j = 1; j <= h; j++)
			{
				cin >> g[i][j];
				if (g[i][j] == '@')
					sx = i, sy = j;
			}

		}
		//多组数据注意相关状态
		cnt = 1;
		memset(vis, 0, sizeof vis);//vis数组全体清0
		vis[sx][sy] = 1;
		dfs({ sx, sy });
		cout << cnt << endl;
	}
	
	return 0;
}

1219：马走日--dfs

注意:本题需要用到回溯算法，故只能用深度优先搜索

【题目描述】

马在中国象棋以日字形规则移动。

请编写一段程序，给定n×m大小的棋盘，以及马的初始位置(x，y)，要求不能重复经过棋盘上的同一个点，计算马可以有多少途径遍历棋盘上的所有点。

【输入】

第一行为整数T(T < 10)，表示测试数据组数。

每一组测试数据包含一行，为四个整数，分别为棋盘的大小以及初始位置坐标n,m,x,y。(0≤x≤n-1,0≤y≤m-1, m < 10, n < 10)。

【输出】

每组测试数据包含一行，为一个整数，表示马能遍历棋盘的途径总数，0为无法遍历一次。

【输入样例】
1
5 4 0 0
【输出样例】
32

#include<iostream>
using namespace std;
const int N = 1e2 + 10;
int g[N][N];//迷宫数组
bool vis[N][N];//二维标记数组
//方向数组--八个方向
int dx[] = { 1,1,-1,-1,2,2,-2,-2 };
int dy[] = { 2,-2,2,-2,1,-1,1,-1};
int t; int n, m,sx,sy;
int cnt;
void dfs(int px, int py, int depth)
{
	if (depth == n * m)//按照此时的搜索方案已经搜完整个棋盘了
	{
		cnt++;
		return;
	}
	for (int i = 0; i < 8; i++)/*注意：八个方向*/
	{
		int bx = px + dx[i], by = py + dy[i];
		if (vis[bx][by])continue;
		if (bx<1 || bx>n || by<1 || by>m)continue;
		vis[bx][by] = 1;
		dfs(bx, by,depth+1);
		//回溯
		vis[bx][by] = 0;
	}

}
int main()
{
	cin >> t;
	while (t--)
	{
		cin >> n >> m;
		//多组数据相关状态清空
		cnt =0;
		cin >> sx >> sy;
		sx++, sy++;
		memset(vis, 0, sizeof vis);
		vis[sx][sy] = 1;
		dfs(sx, sy,1);//起点是第一层，最后应该走到n*m层结束
		cout << cnt << endl;
	}
	return 0;
}

1212：LETTERS--dfs

【题目描述】

给出一个row×col��×��的大写字母矩阵，一开始的位置为左上角，你可以向上下左右四个方向移动，并且不能移向曾经经过的字母。问最多可以经过几个字母。

【输入】

第一行，输入字母矩阵行数R�和列数S�，1≤R,S≤201≤�,�≤20。

接着输出R�行S�列字母矩阵。

【输出】

最多能走过的不同字母的个数。

【输入样例】
3 6
HFDFFB
AJHGDH
DGAGEH
【输出样例】
6

#include<iostream>
using namespace std;
char g[N][N];
bool vis[N];
int dx[] = { 1,-1,0,0};
int dy[] = { 0,0,1,-1};
int n, m;
int ans = 0;
void dfs(int px,int py,int depth)
{
	ans = max(ans, depth);//选取经过字母数最多的
	for (int i = 0; i < 4; i++)
	{
		int bx = px + dx[i], by = py + dy[i];
		if (vis[g[bx][by]])continue;
		if (bx<1 || bx>n || by<1 || by>m) continue;
		vis[g[bx][by]] = 1;
		dfs(bx, by, depth + 1);
		vis[g[bx][by]] =0;//回溯
	}
}
int main()
{
	cin >> n >> m;
	for (int i = 1; i <= n; i++)
	{
		for (int j = 1; j <= m; j++)
		{
			cin >> g[i][j];
		}
	}
	vis[g[1][1]] = 1;
	dfs(1,1,1);
	cout << ans;
	return 0;
}

求最短路径

1251：仙岛求药--bfs

【题目描述】

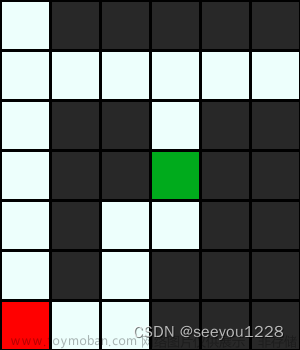
少年李逍遥的婶婶病了，王小虎介绍他去一趟仙灵岛，向仙女姐姐要仙丹救婶婶。叛逆但孝顺的李逍遥闯进了仙灵岛，克服了千险万难来到岛的中心，发现仙药摆在了迷阵的深处。迷阵由M×N个方格组成，有的方格内有可以瞬秒李逍遥的怪物，而有的方格内则是安全。现在李逍遥想尽快找到仙药，显然他应避开有怪物的方格，并经过最少的方格，而且那里会有神秘人物等待着他。现在要求你来帮助他实现这个目标。

下图显示了一个迷阵的样例及李逍遥找到仙药的路线。

【输入】

输入有多组测试数据. 每组测试数据以两个非零整数 M 和 N 开始，两者均不大于20。M 表示迷阵行数, N 表示迷阵列数。接下来有 M 行, 每行包含N个字符,不同字符分别代表不同含义:

1)‘@’：少年李逍遥所在的位置；

2)‘.’：可以安全通行的方格；

3)‘#’：有怪物的方格；

4)‘*’：仙药所在位置。

当在一行中读入的是两个零时，表示输入结束。

【输出】

对于每组测试数据，分别输出一行，该行包含李逍遥找到仙药需要穿过的最少的方格数目(计数包括初始位置的方块)。如果他不可能找到仙药, 则输出 -1。

【输入样例】
8 8
.@##...#
#....#.#
#.#.##..
..#.###.
#.#...#.
..###.#.
...#.*..
.#...###
6 5
.*.#.
.#...
..##.
.....
.#...
....@
9 6

.#..#.
.#.*.#
.####.
..#...
..#...
..#...
..#...
#.@.##
.#..#.
0 0
【输出样例】

10
8
-1

#include<iostream>
#include<queue>
using namespace std;
const int N = 1e2 + 10;
int n, m,sx,sy,tx,ty;
char g[N][N];
bool vis[N][N];
int ans = -1;
int dx[] = { 0,0,1,-1 };
int dy[] = { 1,-1,0,0 };
struct point { int x, y, depth; };
void bfs(point p) {
	queue<point> q;
	q.push(p);  vis[p.x][p.y] = 1;
	while (!q.empty()) {
		point cur = q.front(); q.pop();
		if (cur.x == tx && cur.y == ty) {
			ans= cur.depth - 1;
			return;
		}
		for (int i = 0; i < 4; i++) {
			int bx = cur.x + dx[i], by = cur.y + dy[i];
			if (bx<1 || bx>n || by<1 || by>m) continue;
			if (vis[bx][by]) continue;
			if (g[bx][by] == '#') continue;
			vis[bx][by] = 1;
			q.push({ bx,by,cur.depth + 1 });
		}
	}
}
int main() {
	while (cin >> n >> m && n && m) {
		for (int i = 1; i <= n; i++) {
			for (int j = 1; j <= m; j++) {
				cin >> g[i][j];
				if (g[i][j] == '@') sx = i, sy = j;
				if (g[i][j] == '*') tx = i, ty = j;
			}
		}
		ans = -1;
		memset(vis, 0, sizeof vis);
		bfs({ sx,sy,1 });
		cout << ans << endl;
	}
	return 0;
}

1330：【例8.3】最少步数--bfs

【题目描述】

在各种棋中，棋子的走法总是一定的，如中国象棋中马走“日”。有一位小学生就想如果马能有两种走法将增加其趣味性，因此，他规定马既能按“日”走，也能如象一样走“田”字。他的同桌平时喜欢下围棋，知道这件事后觉得很有趣，就想试一试，在一个（100×100）的围棋盘上任选两点A、B，A点放上黑子，B点放上白子，代表两匹马。棋子可以按“日”字走，也可以按“田”字走，俩人一个走黑马，一个走白马。谁用最少的步数走到左上角坐标为(1,1)的点时，谁获胜。现在他请你帮忙，给你A、B两点的坐标，想知道两个位置到（1,1）点可能的最少步数。

【输入】

A、B两点的坐标。

【输出】

最少步数。

【输入样例】
12 16
18 10
【输出样例】
8
9

#include<iostream>
#include<queue>
const int N = 1e2 + 10;
char g[N][N];
bool vis[N][N];
int dx[] = {1,1,-1,-1,2,2,-2,-2,2,2,-2,-2};
int dy[] = {2,-2,2,-2,1,-1,1,-1,2,-2,2,-2};
int n, m;
int sx, sy;
int ans;
struct point
{
	int x, y,depth;
};
void bfs(point s)
{
	queue<point>q;
	q.push(s); vis[s.x][s.y] = 1;
	while (!q.empty())
	{
		point cur = q.front(); q.pop();
		if (cur.x == 1 && cur.y == 1)
		{
			ans=cur.depth - 1 ;
			return;
		}
		for (int i = 0; i < 12; i++)
		{
			int bx = cur.x + dx[i], by = cur.y + dy[i];
			if (bx<1 || bx>100 || by<1 || by>100)continue;
			if (vis[bx][by])continue;//注意，搜索时也不能搜0
			vis[bx][by] = 1;
			q.push({ bx, by,cur.depth+1});
		}
	}
}

int main()
{
	int t = 2;
	while (t--)
	{
		ans = 0;
		cin >> sx>>sy;
		memset(vis, 0, sizeof vis);
		bfs({ sx, sy ,1});
		cout << ans<<endl;
	}
	return 0;
}

1255：迷宫问题--bfs

【题目描述】
定义一个二维数组：
int maze[5][5] = {
0,1,0,0,0,
0,1,0,1,0,
0,0,0,0,0,
0,1,1,1,0,
0,0,0,1,0,
};
它表示一个迷宫，其中的1表示墙壁，0表示可以走的路，只能横着走或竖着走，不能斜着走，要求编程序找出从左上角到右下角的最短路线。
【输入】

一个5 × 5的二维数组，表示一个迷宫。数据保证有唯一解。

【输出】

左上角到右下角的最短路径，格式如样例所示。

【输入样例】
0 1 0 0 0
0 1 0 1 0
0 0 0 0 0
0 1 1 1 0
0 0 0 1 0
【输出样例】
(0, 0)
(1, 0)
(2, 0)
(2, 1)
(2, 2)
(2, 3)
(2, 4)
(3, 4)
(4, 4)

#include<iostream>
#include<queue>
using namespace std;
const int N = 1e2 + 10;
char g[N][N];
bool vis[N][N];
int dx[] = {0,0,1,-1};
int dy[] = {1,-1,0,0};
struct point
{
	int x, y;
};
point path[N][N];
void bfs(point s)
{
	queue<point>q;
	q.push(s); vis[s.x][s.y] = 1;
	while (!q.empty())
	{
		point cur = q.front(); q.pop();
		if (cur.x == 5 && cur.y == 5)return;
		for (int i = 0; i < 4; i++)
		{
			int bx = cur.x + dx[i], by = cur.y + dy[i];
			if (bx < 1 || bx>5 || by < 1 || by>5)continue;
			if (g[bx][by] == '1')continue;
			if (vis[bx][by])continue;
			vis[bx][by] = 1;
			path[bx][by] = cur;
			q.push({bx, by});
		}
	}
}
void print(int px,int py)
{
	if (px == 0 && py == 0)return;
	print(path[px][py].x, path[px][py].y);
	printf("(%d, %d)\n", px-1, py-1);
}
int main()
{
	for (int i = 1; i <= 5; i++)
		for (int j = 1; j <= 5; j++)
			cin >> g[i][j];
	bfs({1,1});
	print(5,5);
	return 0;
}

1257：Knight Moves

【题目描述】

输入n�代表有个n×n�×�的棋盘，输入开始位置的坐标和结束位置的坐标，问一个骑士朝棋盘的八个方向走马字步，从开始坐标到结束坐标可以经过多少步。图论之dfs与bfs的练习,题解,深度优先,图论,宽度优先

【输入】

首先输入一个n�,表示测试样例的个数。

每个测试样例有三行。

第一行是棋盘的大小L(4≤L≤300)�(4≤�≤300)；

第二行和第三行分别表示马的起始位置和目标位置(0..L−1)(0..�−1)。

【输出】

马移动的最小步数，起始位置和目标位置相同时输出00。

【输入样例】

【输出样例】文章来源地址https://www.toymoban.com/news/detail-830128.html

5
28
0

#include<iostream>
#include<queue>
//#include<Windows.h>//动画演示
using namespace std;
const int N = 3e2 + 10;
char g[N][N];
bool vis[N][N];
int dx[] = {1,1,2,2,-1,-1,-2,-2};
int dy[] = {2,-2,1,-1,2,-2,1,-1};
int t;
int n,sx, sy, tx, ty;
int ans;
struct point { int x; int y; int depth; };
void dfs(point s)
{
	queue<point>q;
	q.push(s); vis[s.x][s.y] = 1;
	while (!q.empty())
	{
		point cur = q.front(); q.pop();
		if (cur.x == tx && cur.y == ty)
		{
			ans = cur.depth-1;
			return;
		}
		for (int i = 0; i < 8; i++)
		{
			int bx = cur.x + dx[i], by = cur.y + dy[i];
			if (bx<1 || bx> n || by<1 || by>n) continue;
			if (vis[bx][by]) continue;
			vis[bx][by] = 1;
			
			q.push({ bx, by,cur.depth+1 });
		}
	}
	
}

int main()
{
	cin >> t;
	while (t--)
	{
		cin >> n;
		cin >> sx >> sy >> tx >> ty;
		sx++, sy++,tx++, ty++;
		ans = 0;
		memset(vis, 0, sizeof vis);
		dfs({ sx, sy,1 });
		cout << ans<<endl;
	}
	return 0;
}

到了这里，关于图论之dfs与bfs的练习的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！