数据结构与算法：双向链表-Toy模板网

这篇具有很好参考价值的文章主要介绍了数据结构与算法：双向链表。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

朋友们大家好啊，在上节完成单链表的讲解后，我们本篇文章来对带头循环双向链表进行讲解

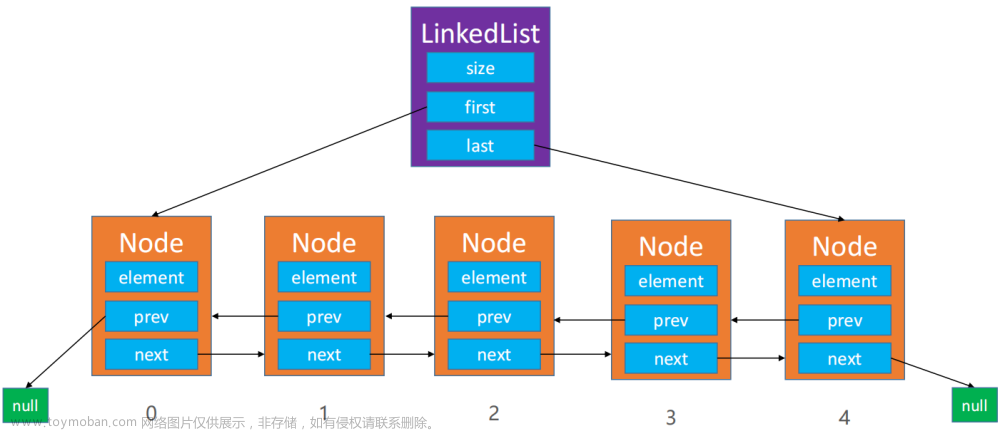
双向链表、头节点和循环的介绍

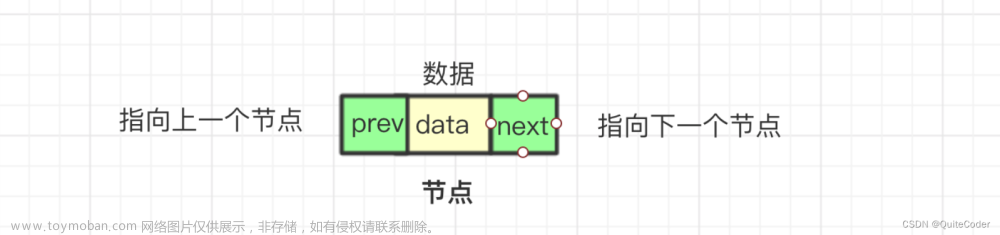
数据结构与算法：双向链表,数据结构
单链表中，一个节点存储数据和指向下一个节点的指针，而双向链表除了上述两个内容，还包括了指向上一个节点的指针

带头的双向链表，是指在双向链表的最前端添加了一个额外的节点，这个节点被称为头节点（哨兵节点），但它一般不用于存储实际的数据（或者可以说存储的数据不被使用）。头节点的主要目的是为了简化链表操作的逻辑，避免在处理链表的开始和结束位置时需要进行特殊的条件判断。

在没有头节点的普通双向链表中，如果链表为空，则链表的第一个节点（head pointer）直接为NULL，这使得插入和删除操作时，需要分别检查特定情况，如链表是否为空、是否在链表开始或结束位置进行操作等。

循环链表，即最后一个节点指向下一个节点的指针并不指向空，而是指向头结点，且头结点的指向上一个节点的指针也并不指向空，而是指向最后一个节点

简单介绍之后，我们就来讲解双向循环链表的各个细节吧

构建双向链表

typedef int LTDatatype;

typedef struct ListNode
{
	struct ListNode* next;
	struct ListNode* prev;
	LTDatatype val;
}LTNode;

这里typedef int LTDatatype;我们多次提到，为类型抽象

构建的节点中，每个节点包括两个指针：

struct ListNode* next;：
这是一个指针，指向下一个ListNode节点。在链表中，每个节点通过这样的next指针连接到下一个节点。对于链表的最后一个节点，这个指针通常设为NULL，表示没有后续节点。但在循环链表的情况下，最后一个节点的next指针会指向链表的第一个节点，形成一个闭环。
struct ListNode* prev;
这是另一个指针，指向前一个ListNode节点。在双向链表中，除了能够向前遍历，我们还可以通过这个prev指针向后遍历链表。对于链表的第一个节点，这个指针在非循环链表中通常设为NULL，表示没有前驱节点**。而在循环链表中，第一个节点的prev指针会指向链表的最后一个节点。**

节点的构建

我们首先定义一个函数

LTNode* CreatNode(LTDatatype x)；

与单链表不同的是，这个函数多了一个指向前一个节点的指针，其他内容均相同

LTNode* CreatNode(LTDatatype x)
{
	LTNode* newnode = (LTNode*)malloc(sizeof(LTNode));
	if (newnode == NULL)
	{
		perror("malloc fail");
		exit(-1);
	}
	newnode->val = x;
	newnode->next = NULL;
	newnode->prev = NULL;
	return newnode;
}

初始化双向循环链表（空链表）

在双向循环链表中，空链表的标志性质是其头节点的 next 和 prev指针都指向它自身。即使是空的链表，依然保持着循环的特性，但它不包含任何数据节点，只有这一个特殊的头节点

这里有两种初始化的形式

void LTInit(LTNode** phead)
{
    *phead = (LTNode*)malloc(sizeof(LTNode)); 
    if (*phead != NULL) {
        (*phead)->next = *phead;
        (*phead)->prev = *phead; 
     }
}

phead 代表指向链表的“头节点”的指针

在这个初始化函数中，新创建的链表头节点的 next 和 prev 指针都被设置为指向自身，形成一个空的双向循环链表，这里用了二级指针，是因为我们对phead进行了改变，对指针进行改变，则需要二级指针
这种方法我们初始化格式如下，首先创造一个plist结构体指针，再传参

LTNode* plist;
LTInit(&plist);

LTNode* LTInit2() {
    LTNode* phead = (LTNode*)malloc(sizeof(LTNode));
    if (phead != NULL) {
        phead->prev = phead;
        phead->next = phead;
    }
    return phead; 
}

在这个实现中，LTInit函数不接受任何参数，而是直接创建并初始化一个新的头节点，使其prev和next指针都指向自己，从而形成一个空的双向循环链表。这样设计的好处是简化了链表的初始化过程，你只需要调用LTInit来获取一个新的链表头节点即可
这种方法我们直接用plist接收返回值即可

LTNode* plist=LITnit2();

销毁双向链表

void ListDestroy(LTNode* phead) {
    if (phead == NULL) {
        return;
    }
    // 由于是循环链表，我们需要一个指针指向第一个节点
    LTNode* current = phead->next;
    // 如果链表不只是头节点自己循环（即有实际数据节点）
    if (current != phead) {
        do {
            LTNode* temp = current;
            current = current->next; // 移动到下一个节点
            free(temp); // 释放当前节点内存
        } while (current != phead);
    }
    // 最后，释放头节点内存（如果头节点是哨兵节点并且是动态分配的）
    free(phead);
}

函数首先检查传入的链表是否为空。如果不为空，它会进入一个 do-while 循环，这个循环确保至少运行一次，即使链表中只有一个节点（头节点）
在循环内部，它会释放当前节点的内存，并移动到下一个节点，直到它循环回到头节点。最后，它释放头节点的内存

链表的打印

在单链表中，我们进行循环打印的判断条件是最后一个节点的指针是否指向NULL，而在双向循环链表中，没有空指针，我们的判断条件也有所不同

void LTPrint(LTNode* phead) {
    if (phead == NULL || phead->next == phead) {
        return;
    }
    LTNode* current = phead->next;
    while (current != phead) { 
        printf("%d ", current->val); 
        current = current->next; 
    }
    printf("\n"); 
}

首先

if (phead == NULL || phead->next == phead) {
    return;
}

这串代码是判断链表是否为空或者链表是否只有一个头结点，如果是，则没有数据可打印，直接返回

遍历链表:

LTNode* current = phead->next;
while (current != phead) { 
    printf("%d ", current->val); 
    current = current->next; 
}

这部分代码初始化一个新指针 current 指向链表的第一个节点（即 phead->next），然后进入一个 while 循环。在循环中，只要 current 不指回 phead，它就打印当前节点的值，并移动到下一个节点。这个循环确保了所有节点都被访问一次。

注意，由于它从 phead->next 开始，phead 本身不存储有效数据（或者说是一个哨兵节点）

双向链表头尾的插与删

尾插

void LTPushBack(LTNode* phead, LTDatatype x) {
    LTNode* newnode = CreatNode(x);
    if (phead == NULL) {
        return;
    }
    newnode->next = phead; 
    newnode->prev = phead->prev;
    phead->prev->next = newnode;
    phead->prev = newnode;
}

数据结构与算法：双向链表,数据结构
我们构建newnode

newnode的next指向头结点： newnode->next = phead;
原来的phead的prev指针指向倒数第二个节点，那么newnode的前一个指针则为初始时phead的prev指针：newnode->prev = phead->prev;
现在更新倒数第二个节点的下一个指针，原来指向头指针，现在指向newnode：phead->prev->next = newnode;
最后更改phead的prev指针，指向尾部的newnode：phead->prev = newnode;

测试代码如下：
数据结构与算法：双向链表,数据结构

尾删

void LTPopBack(LTNode* phead) {
     if (phead == NULL || phead->next == phead) {
        return;
    }
    LTNode* tail = phead->prev; 
    LTNode* tailprev = tail->prev; 

    // 断开当前末尾节点与链表的连接，形成新的末尾
    tailprev->next = phead;
    phead->prev = tailprev;

    // 释放原末尾节点占用的内存
    free(tail);
}

首先判断是否为空链表或者只有哨兵节点，如果是则没有值可以删除，直接返回
找到尾部节点tail，即头结点的前一个指针指向的节点；
再找到tail前面的节点，即预期的尾节点，将这个节点的下一个指针指向头结点，并将头节点的前一个指针指向这个节点
将tail这个尾部节点内存释放

测试代码如下:
数据结构与算法：双向链表,数据结构

头插

void LTPushFront(LTNode* phead, LTDatatype x) {
    LTNode* newnode = CreatNode(x); 
    if (phead == NULL) {
        return;
    }
    newnode->next = phead->next; 
    newnode->prev = phead;       
    phead->next->prev = newnode; 
    phead->next = newnode;       
}

首先判断链表是否为空，为空直接返回
新节点的next指针指向原来头节点的下一个节点：newnode->next = phead->next;
新节点的prev指针指向头结点：newnode->prev = phead;
接着更新头节点之后的节点的prev指针，以及头节点的next指针
- 原来头节点之后的节点的prev指针现在应该指向新节点：phead->next->prev = newnode;
- 头节点的next指针现在应该指向新节点：phead->next = newnode;

我们更新了四个指针：新节点的前后指针，头结点的next指针，后一个节点的prev指针

测试代码：
数据结构与算法：双向链表,数据结构

头删

void LTPopFront(LTNode* phead) {
    if (phead == NULL || phead->next == phead) {
        return;
    }
    LTNode* first = phead->next;
    phead->next = first->next;
    first->next->prev = phead;
    free(first);
}

首先检查链表是否为空或者只有哨兵节点
找到要删除的节点，它是头节点的下一个节点：LTNode* first = phead->next;
更新头节点的next指向被删除节点的下一个节点：phead->next = first->next;
更新新的第一个有效数据节点的prev指向头节点：first->next->prev = phead;
最后释放被删除节点所占用的内存

测试代码：
数据结构与算法：双向链表,数据结构

查找特定节点

LTNode* ListFind(LTNode* phead, int x) {
    if (phead == NULL || phead->next == phead) {
        return NULL;
    }
    LTNode* current = phead->next; 
    while (current != phead) { 
        if (current->val == x) {
            return current;
        }
        current = current->next; 
    }
    return NULL;
}

如果链表为空或者只有哨兵节点，直接返回
由于第一个节点没有有效数据，我们可以从 phead 的下一个节点开始遍历
在这个实现中，我们从哨兵节点的下一个节点开始遍历，即从链表的第一个实际数据节点开始。循环继续执行，直到 current 指针再次回到哨兵节点 phead。如果找到一个节点的值与 x 相等，函数返回该节点的指针。如果遍历完所有节点都没有找到，则返回 NULL。

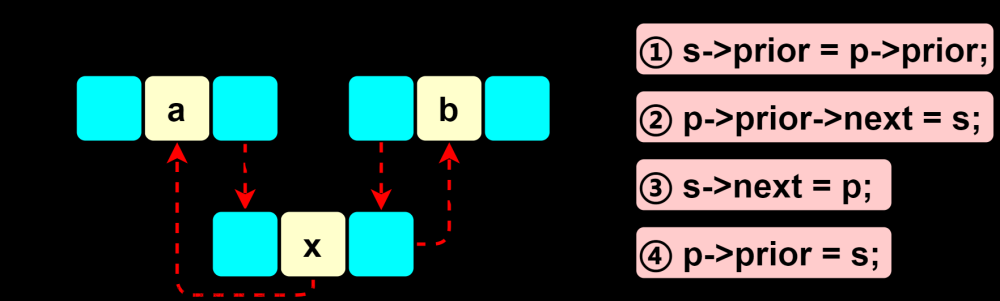
在指定位置前插入数据

void ListInsert(LTNode* pos, LTDatatype x)
{
    if (pos == NULL)
    {
        return;
    }
    LTNode* posprev = pos->prev;
    LTNode* newnode = CreatNode(x);

    posprev->next = newnode;
    newnode->prev = posprev;
    newnode->next = pos;
    pos->prev = newnode;
}

找到pos前面的节点posprev
构建新节点
posprev的next指针指向newnode；
newnode的prev指针指向posprev，next指针指向pos
pos的前一个指针指向newnode；

测试代码，在1 2 3 4 5的3前面插入8，首先获得3节点的地址，在传入插入函数中

数据结构与算法：双向链表,数据结构
如果再哨兵节点位置，往前插入，则相当于尾插

删除pos节点

我们假设pos不为哨兵节点

void ListErase(LTNode* pos) {
    if (pos == NULL) {
        return;
    }
    pos->prev->next = pos->next;
    pos->next->prev = pos->prev;
    free(pos);
}