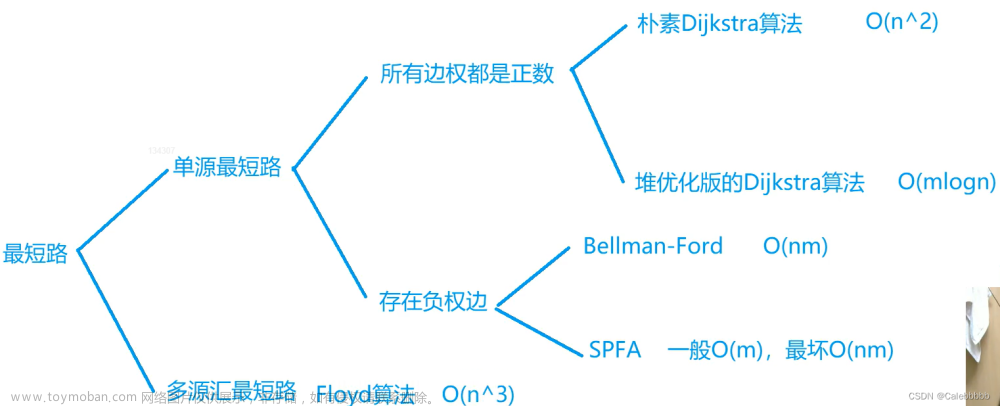
找负环（图论基础）-Toy模板网

这篇具有很好参考价值的文章主要介绍了找负环（图论基础）。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

负环

找负环（图论基础）,图论,SPFA,图论,spring boot,fastapi,django,flask,numpy,spring
环内路径上的权值和为负。

spfa找负环

两种基本的方法

统计每一个点的入队次数，如果一个点入队了n次，则说明存在负环
统计当前每个点中的最短路中所包含的边数，如果当前某个点的最短路所包含的边数大于等于n，也说明存在负环

实际上两种方法是等价的，都是判断是否路径包含n条边， $n$ 条边的话就有 $n + 1$ 个点
用的更多的还是第二种方法。

方法一

$c n t [x] : 表示 x 的入队次数$

#include <bits/stdc++.h> 
#define int long long
#define rep(i,a,b) for(int i = (a); i <= (b); ++i)
#define fep(i,a,b) for(int i = (a); i >= (b); --i)
#define pii pair<int, int>
#define ll long long
#define db double
#define endl '\n'
#define x first
#define y second
#define pb push_back
#define inf 0x3f3f3f3f*1ll

using namespace std;

void solve()
{
	int n,m1,m2;
	cin>>n>>m1>>m2;
	vector<vector<pii>>g(n+1);
	rep(i,1,m1){
		int u,v,w;
		cin>>u>>v>>w;
		g[u].pb({v,w});
		g[v].pb({u,w});
	}	
	rep(i,1,m2){
		int u,v,w;
		cin>>u>>v>>w;
		g[u].pb({v,-w});
	}
	vector<int>inq(n+1,0);
	vector<int>cnt(n+1,0);
	vector<int>d(n+1,0);
	queue<int>q;
	rep(i,1,n){
		q.push(i);
		inq[i]=1;
	}
	while(q.size()){
		auto t=q.front();
		q.pop();
		int u=t;
		inq[u]=0;
		for(auto it:g[u]){
			int v=it.x,w=it.y;
			if(d[v]>d[u]+w){
				d[v]=d[u]+w;
				if(!inq[v]){
					q.push(v);
					inq[v]=1;
					cnt[v]++;
					if(cnt[v]>=n){
					cout<<"YES"<<endl;
					return;
					}
				}
			}
		}
	}
	cout<<"NO"<<endl;
}

signed main(){
	ios::sync_with_stdio(false); cin.tie(0); cout.tie(0);
//   	freopen("1.in", "r", stdin);
	int _;
	cin>>_;
	while(_--)
	solve();
	return 0;
}

方法二

$c n t [x] : 表示从起点到 x 所经过的最短路径的边数$

#include <bits/stdc++.h> 
#define int long long
#define rep(i,a,b) for(int i = (a); i <= (b); ++i)
#define fep(i,a,b) for(int i = (a); i >= (b); --i)
#define pii pair<int, int>
#define ll long long
#define db double
#define endl '\n'
#define x first
#define y second
#define pb push_back
#define inf 0x3f3f3f3f*1ll

using namespace std;

void solve()
{
	int n,m1,m2;
	cin>>n>>m1>>m2;
	vector<vector<pii>>g(n+1);
	rep(i,1,m1){
		int u,v,w;
		cin>>u>>v>>w;
		g[u].pb({v,w});
		g[v].pb({u,w});
	}	
	rep(i,1,m2){
		int u,v,w;
		cin>>u>>v>>w;
		g[u].pb({v,-w});
	}
	vector<int>inq(n+1,0);
	vector<int>cnt(n+1,0);
	vector<int>d(n+1,0);
	queue<int>q;
	rep(i,1,n){
		q.push(i);
		inq[i]=1;
	}
	while(q.size()){
		auto t=q.front();
		q.pop();
		int u=t;
		inq[u]=0;
		for(auto it:g[u]){
			int v=it.x,w=it.y;
			if(d[v]>d[u]+w){
				d[v]=d[u]+w;
				cnt[v]=cnt[u]+1;
				if(cnt[v]>=n){
					cout<<"YES"<<endl;
					return;
				}
				if(!inq[v]){
					q.push(v);
					inq[v]=1;
				}
			}
		}
	}
	cout<<"NO"<<endl;
}

signed main(){
	ios::sync_with_stdio(false); cin.tie(0); cout.tie(0);
//   	freopen("1.in", "r", stdin);
	int _;
	cin>>_;
	while(_--)
	solve();
	return 0;
}

实际效果

找负环（图论基础）,图论,SPFA,图论,spring boot,fastapi,django,flask,numpy,spring

方法一跑出来的结果是 $1024 m s$
方法二跑出来的结果是 $671 m s$ 文章来源地址https://www.toymoban.com/news/detail-830363.html