C F 786 B − L e g a c y \mathrm{CF786B - Legacy} CF786B−Legacy
D e s c r i p t i o n \mathrm{Description} Description
给定 1 1 1 张 n n n 个点的有向图,初始没有边,接下来有 q q q 次操作,形式如下:
-
1 u v w表示从 u u u 向 v v v 连接 1 1 1 条长度为 w w w 的有向边 -
2 u l r w表示从 u u u 向 i i i( i ∈ [ l , r ] i\in [l,r] i∈[l,r])连接 1 1 1 条长度为 w w w 的有向边 -
3 u l r w表示从 i i i( i ∈ [ l , r ] i\in [l,r] i∈[l,r])向 u u u 连接 1 1 1 条长度为 w w w 的有向边
输出从 S S S 点到 i i i 点( i ∈ [ 1 , n ] i\in [1,n] i∈[1,n])的最短路长度。
S o l u t i o n \mathrm{Solution} Solution
观察可知,最多会建立 1 0 5 × 1 0 5 = 1 0 10 10^5\times 10^5 = 10^{10} 105×105=1010 条边,故必定超时。
此时,需要使用 线段树优化建图,这里展开简单说一下:
对于 1 1 1 棵存储点为 1 ∼ 4 1\sim 4 1∼4 的线段树,形式如下:
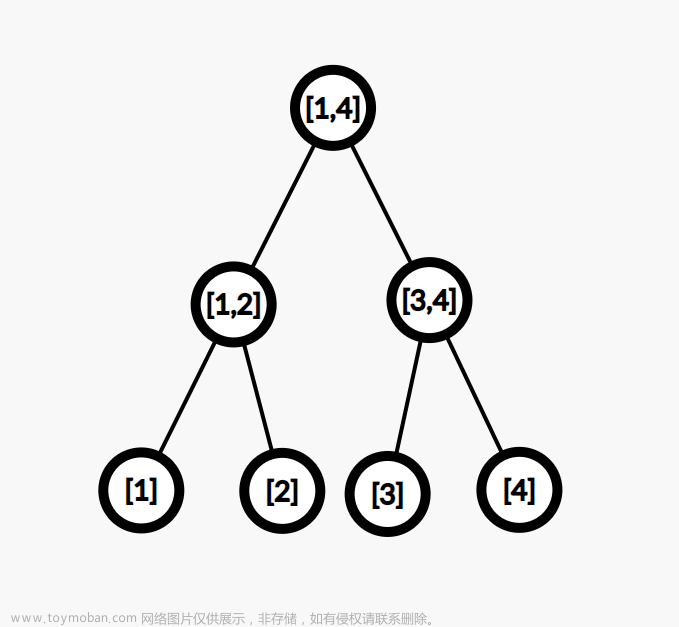
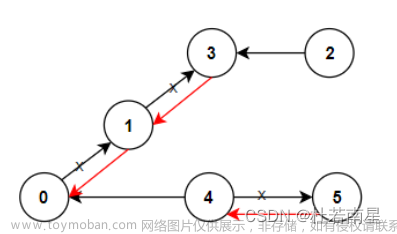
如果当前为 2 2 2 操作,且为 1 ∼ 3 1\sim 3 1∼3 每个点连向 4 4 4,权值为 10 10 10,操作如下所示:

即,将区间 1 ∼ 2 1\sim 2 1∼2 和 3 ∼ 3 3\sim 3 3∼3 连向 4 4 4 即可,不过此时发现,图中为有向图,而现在是无向图所以我们要对于图中的每一条边标记方向和权值(这里线段树就是一张图,叶子节点就是我们的 1 ∼ n 1\sim n 1∼n 节点)

其中,为何线段树上的边方向都为向父亲节点?那是因为 1 1 1, 2 2 2 号点只有这样才能顺着边走到 4 4 4 号节点,对于为何权值设为 0 0 0,因为这是 1 1 1 条虚边(不存在的),不能对最短路做出任何贡献。文章来源:https://www.toymoban.com/news/detail-830504.html
不过,上文是区间连节点,当是节点连区间的时候(操作 3 3 3)边都是正好反着的,所以再建 1 1 1 棵线段树即可(不过没必要真的去再建 1 1 1 棵,具体见代码)文章来源地址https://www.toymoban.com/news/detail-830504.html
C o d e Code Code
#include <bits/stdc++.h>
#define int long long
using namespace std;
typedef pair<int, int> PII;
typedef long long LL;
const int SIZE = 4e6 + 10, SIZE2 = 1e6 + 10;
int N, Q, S;
int h[SIZE2], e[SIZE], ne[SIZE], w[SIZE], idx;
int Id[2], Dist[SIZE2], Vis[SIZE2];
struct Segment
{
int l, r;
int L, R;
}Tree[SIZE2 << 2];
void add(int a, int b, int c)
{
e[idx] = b, ne[idx] = h[a], w[idx] = c, h[a] = idx ++;
}
int Build(int l, int r, int Sd, int k)
{
if (l == r)
{
Tree[l] = {l, l};
return l;
}
int P = ++ Id[k];
Tree[P] = {l, r};
int mid = l + r >> 1;
Tree[P].L = Build(l, mid, Sd, k), Tree[P].R = Build(mid + 1, r, Sd, k);
if (!Sd) add(Tree[P].L, P, 0), add(Tree[P].R, P, 0);
else add(P, Tree[P].L, 0), add(P, Tree[P].R, 0);
return P;
}
void Add(int u, int l, int r, int p, int w, int Sd)
{
if (Tree[u].l >= l && Tree[u].r <= r)
{
if (!Sd) add(u, p, w);
else add(p, u, w);
return;
}
int mid = Tree[u].l + Tree[u].r >> 1;
if (mid >= l) Add(Tree[u].L, l, r, p, w, Sd);
if (mid < r) Add(Tree[u].R, l, r, p, w, Sd);
}
void Dijkstra(int S)
{
memset(Dist, 0x3f, sizeof Dist);
memset(Vis, 0, sizeof Vis);
priority_queue<PII, vector<PII>, greater<PII>> Heap;
Heap.push({0, S}), Dist[S] = 0;
while (Heap.size())
{
auto Tmp = Heap.top();
Heap.pop();
int u = Tmp.second;
if (Vis[u]) continue;
Vis[u] = 1;
for (int i = h[u]; ~i; i = ne[i])
{
int j = e[i];
if (Dist[j] > Dist[u] + w[i])
{
Dist[j] = Dist[u] + w[i];
Heap.push({Dist[j], j});
}
}
}
}
signed main()
{
cin.tie(0);
cout.tie(0);
ios::sync_with_stdio(0);
memset(h, -1, sizeof h);
cin >> N >> Q >> S;
if (N == 1)
{
cout << 0 << endl;
return 0;
}
Id[0] = N;
Build(1, N, 0, 0);
Id[1] = Id[0];
Build(1, N, 1, 1);
while (Q --)
{
int Op, v, u, l, r, w;
cin >> Op >> u;
if (Op == 1)
{
cin >> v >> w;
add(u, v, w);
}
else if (Op == 2)
{
cin >> l >> r >> w;
Add(Id[0] + 1, l, r, u, w, 1);
}
else
{
cin >> l >> r >> w;
Add(N + 1, l, r, u, w, 0);
}
}
Dijkstra(S);
for (int i = 1; i <= N; i ++)
if (Dist[i] >= 1e18) cout << -1 << " ";
else cout << Dist[i] << " ";
return 0;
}
到了这里,关于【图论经典题目讲解】CF786B - Legacy 一道线段树优化建图的经典题目的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!