leetcode(算法) 70.爬楼梯（python版）-Toy模板网

这篇具有很好参考价值的文章主要介绍了leetcode(算法) 70.爬楼梯（python版）。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

需求

假设你正在爬楼梯。需要 n 阶你才能到达楼顶。
每次你可以爬 1 或 2 个台阶。你有多少种不同的方法可以爬到楼顶呢？
示例 1：
输入：n = 2
输出：2
解释：有两种方法可以爬到楼顶。

1 阶 + 1 阶
2 阶
示例 2：
输入：n = 3
输出：3
解释：有三种方法可以爬到楼顶。
1 阶 + 1 阶 + 1 阶
1 阶 + 2 阶
2 阶 + 1 阶

分析

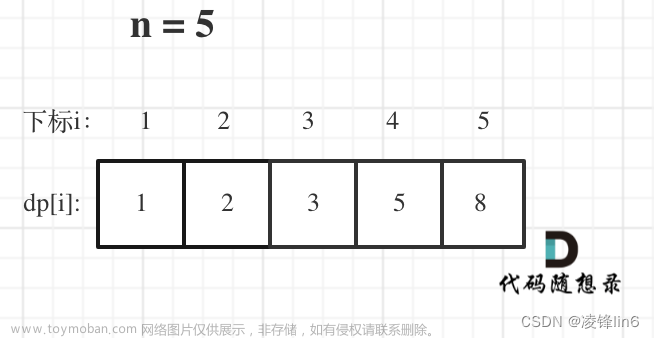
创建了一个动态规划数组dp，其中dp[i]表示到达第i阶楼梯的方法数。
初始时，dp[0]和dp[1]分别为1（只有一种方式到达第1阶楼梯）和2（有两种方式到达第2阶楼梯）。
然后，对于更高阶的楼梯，其方法数等于前两阶楼梯的方法数之和。最后返回dp[n-1]，即为到达楼顶的方法数。

代码

class Solution:
    """
    创建了一个动态规划数组dp，其中dp[i]表示到达第i阶楼梯的方法数。
    初始时，dp[0]和dp[1]分别为1（只有一种方式到达第1阶楼梯）和2（有两种方式到达第2阶楼梯）。
    然后，对于更高阶的楼梯，其方法数等于前两阶楼梯的方法数之和。最后返回dp[n-1]，即为到达楼顶的方法数。
    """
    def climb_stairs(self,n):
        if n==1:
            return 1
        if n==2:
            return 2
        # dp 初始化一个长度为n的列表，其中所有元素都被设置为0。
        # dp = [0 for _ in range(n)] 是Python中创建列表的一种简洁写法，它初始化一个长度为n的列表，其中所有元素都被设置为0。
        # range(n)：生成一个从0开始（默认）到n-1结束的整数序列。例如，如果n是3，则range(3)会生成序列[0, 1, 2]。
        # _：在Python中，单下划线 _ 通常用作临时变量名，表示我们并不关心这个变量的具体值。在这个上下文中，我们只是想对range(n)中的每个元素执行操作，但并不需要引用这些索引。
        # [0 for _ in range(n)]：这行代码创建了一个列表推导式，它遍历range(n)中的每个元素（即从0到n-1的所有整数），并将0作为对应位置的元素添加到新列表中。所以，当n=3时，这段代码将生成列表[0, 0, 0]。
        dp=[0 for temp in range(n)]
        dp[0]=1
        dp[1]=2
        for i in range(2,n):
            dp[i]=dp[i-1]+dp[i-2]
        return dp[-1]

if __name__ == '__main__':
    call=Solution()
    print(call.climb_stairs(2))
    print(call.climb_stairs(3))
    print(call.climb_stairs(4))