算法-二叉树相关

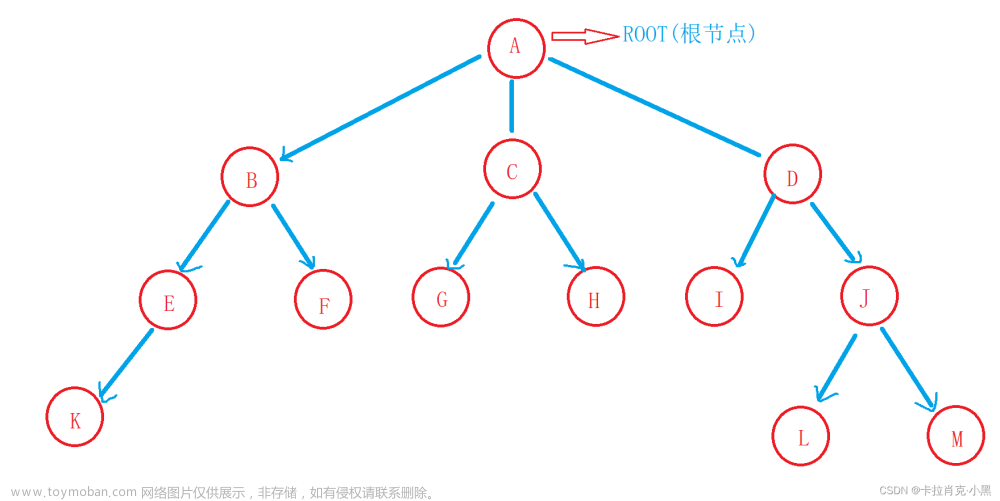
判断二叉树是否是完全二叉树

思路：层次遍历，如果之前某个节点叶子节点为空，队列后续的所有节点的左右节点都不能非空，并且如果节点左节点为null但是右节点不为null该二叉树一定不是满二叉树

public static boolean isCBT1(Node  head) {
        // PC
        if(head == null)
            return true;
        LinkedList<Node > queue = new LinkedList<>();
        boolean isLeaf = false;
        queue.add(head);
        while (!queue.isEmpty()){
            Node  cur = queue.poll();
            Node  left = cur.left;
            Node  right = cur.right;
            if(
                    (isLeaf && (left != null || right != null)) || (left == null && right != null)
            )
                return false;
            if(left != null ){
                queue.add(left);
            }
            if(right != null){
                queue.add(right);
            }
            if(left == null || right == null)
                isLeaf = true;
        }
        return true;
    }

思路2：使用递归方式，返回以当前节点为头结点的二叉树是否是满二叉树|完全二叉树以及返回当前树高度，调用方根据左右子树返回的信息判断当前树是否为完全二叉树

// 使用递归方式
    public static boolean isCBT2(class13.Code01_IsCBT.Node  head) {
        if(head == null)
            return true;
        Info process = process(head);
        return process.isc;

    }
    public static Info process(Node head){
        if (head == null){
            return new Info(true,true,0);
        }
        Info l = process(head.left);
        Info r = process(head.right);
        boolean isFull = l.isf && r.isf && l.height == r.height;
        int height = Math.max(l.height,r.height)+1;
        boolean isComplate = false;
        if(l.height == r.height){
            if((l.isf && r.isf)||(l.isf && r.isc)){
                isComplate = true;
            }
        }else {
            if(l.height == r.height+1){
                if((r.isf && l.isf)||(r.isf && l.isc)){
                    isComplate = true;
                }
            }
        }

        return new Info(isComplate,isFull,height);
    }

    static class Info{
        // 也包括满二叉树场景
        private boolean isc;
        private boolean isf;
        private int height;
        public Info(boolean isc,boolean isf,int height){
            this.isc = isc;
            this.isf = isf;
            this.height = height;
        }
    }

题目：给定一棵二叉树的头节点head，和另外两个节点a和b。返回a和b的最低公共祖先

思路：先序遍历二叉树，过程中记录子节点的父节点，维护在Map类型参数中，然后求第一个相同的祖先

方法2：递归，返回当前节点左右子树是否包含指定节点，如果是直接返回否则根据返回内容处理

static class Info{
        boolean finda;
        boolean findb;
        Node ans ;

        public Info(boolean finda, boolean findb, Node ans) {
            this.finda = finda;
            this.findb = findb;
            this.ans = ans;
        }
    }


    public static Node lowestAncestor1(Node head, Node o1, Node o2) {
        // PC
        Info ans = process(head, o1, o2);
        return ans.ans;

    }
    public  static Info process(Node head, Node o1, Node o2){
        if(head == null)
            return new Info(false,false,null);
        Info l = process(head.left,o1,o2);
        Info r = process(head.right,o1,o2);
        boolean finda = head == o1?true:l.finda||r.finda;
        boolean findb = head == o2?true:r.findb||l.findb;
        Node ans = null;
        if(l.ans != null){
            ans = l.ans;
        }else if (r.ans != null){
            ans = r.ans;
        }else {
            if(finda && findb){
                ans = head;
            }
        }
        return new Info(finda,findb,ans);
    }

题目：派对的最大快乐值 公司的每个员工都符合 Employee 类的描述。整个公司的人员结构可以看作是一棵标准的、 没有环的多叉树。树的头节点是公司唯一的老板。除老板之外的每个员工都有唯一的直接上级。 叶节点是没有任何下属的基层员工(subordinates列表为空)，除基层员工外，每个员工都有一个或多个直接下级。派对的最大快乐值这个公司现在要办party，你可以决定哪些员工来，哪些员工不来，规则：1.如果某个员工来了，那么这个员工的所有直接下级都不能来2.派对的整体快乐值是所有到场员工快乐值的累加3.你的目标是让派对的整体快乐值尽量大给定一棵多叉树的头节点boss，请返回派对的最大快乐值。

思路：递归实现

    public static int maxHappy1(Employee boss) {
        // PC
        if(boss == null)
            return 0;
        return Math.max(process(boss,true),process(boss,false));
    }
    // cur 来到当前人员
    // exist 直接领导是否来
    // 返回最大快乐值
    public static  int process(Employee cur,boolean exist){
        if(cur == null)
            return 0;
        // 当前人员选择不来 这种情况和上级领导来或者不来都不影响
        int no = 0;
        for (Employee next : cur.nexts) {
            no += process(next,false);
        }
        int yes = 0;
        // 上级领未来并且当前人员参加
        if(!exist){
            for (Employee next : cur.nexts) {
                yes += process(next,true);
            }
            yes += cur.happy;
        }
        return Math.max(yes,no);
    }

上面递归方式传递参数包含了上级是否参加信息，另外一种递归方式，返回当前人员参加或者不参加两种情况的最大值，由上级决定自己是否参加

static class Info {
        private int no;
        private int yes;

        public Info(int no, int yes) {
            this.no = no;
            this.yes = yes;
        }
    }

    public static int maxHappy2(Employee boss) {
        if (boss == null)
            return 0;
        Info info = process2(boss);
        return Math.max(info.yes, info.no);
    }

    // 返回当前人员参加或者不参加最大happy值
    // 具体如何使用由上层决定
    public static Info process2(Employee cur) {
        if (cur == null)
            return new Info(0, 0);

        int yes = cur.happy;
        int no = 0;
        for (Employee next : cur.nexts) {
            Info info = process2(next);
            no += Math.max(info.no, info.yes);
            yes += info.no;
        }
        return new Info(no, yes);
    }

题目：判断二叉树是否是搜索二叉树

方法1：递归，左右子树返回是否递归相关信息，调用方法根据返回信息判断

    public static boolean isBST1(Node head) {
        if(head == null)
            return true;
        Info info = process(head);
        return info.isSearch;

    }
    // 以当前节点为根节的二叉树，返回是否搜索二叉树信息
    public static Info process(Node head){
        Info left = null;
        if(head.left != null){
            left = process(head.left);
        }
        Info right = null;
        if(head.right != null){
            right = process(head.right);
        }
        int max = head.value;
        int min = head.value;
        if(left != null){
            max = Math.max(max, left.max);
            min = Math.min(min, left.min);
        }
        if(right != null){
            max = Math.max(right.max,max);
            min = Math.min(min, right.min);
        }
        boolean flag = true;

        if(left != null && !left.isSearch)
            flag = false;
        if(right  != null && !right.isSearch)
            flag = false;
        if(left != null && left.max >= head.value)
            flag = false;
        if(right!=null && right.min<= head.value){
            flag = false;
        }

        return new Info(max,min,flag);
    }

    static class Info{
        private int max;
        private int min;
        private boolean isSearch;

        public Info(int max, int min, boolean isSearch) {
            this.max = max;
            this.min = min;
            this.isSearch = isSearch;
        }
    }

方法2：利用二叉搜索树性质，先序遍历一定是递增序列

题目：给定一棵二叉树的头节点head，返回这颗二叉树是不是平衡二叉树

思路：递归方法

    public static boolean isBalanced1(Node head) {
        if(head == null)
            return true;
        Info ans = process(head);
        return ans.isblance;
    }

    // 以当前节点为根节点的二叉树，返回该二叉树是否为平衡二叉树
    public static Info process(Node head){
        if(head == null)
            return new Info(true,0);
        Info l = process(head.left);
        Info r = process(head.right);
        boolean is = false;
        // 不管左右子树是否为平衡二叉树 直接计算，调用方最终需要的不是高度而是 是否平衡
        int height = Math.max(l.height,r.height)+1;
        // process方法返回对象一定不为null
        if(l.isblance && r.isblance && Math.abs(l.height-r.height)<=1){
            is = true;
        }
        return new Info(is,height);

    }
    static class  Info {
        private boolean isblance;
        private Integer height ;

        public Info(boolean isblance, Integer height) {
            this.isblance = isblance;
            this.height = height;
        }
    }

题目：给定一棵二叉树的头节点head，返回这颗二叉树是不是满二叉树

思路：层次遍历上一层和当前层数量二倍关系，特殊情况最后一层遍历时候需要特殊处理

public static boolean isFull1(Node head) {
        if(head == null)
            return true;
        // 层次遍历 判断上一层和当前层数量是否二倍关系
        LinkedList<Node> queue = new LinkedList<>();
        queue.add(head);
        while (!queue.isEmpty()){
            // 用于判断是否为最后一行
            boolean allNull = true;
            int pre = queue.size();
            for (int i = 0; i < pre; i++) {
                Node cur = queue.poll();
                if(cur.left != null){
                    queue.add(cur.left);
                    allNull = false;
                }
                if(cur.right != null){
                    queue.add(cur.right);
                    allNull = false;
                }
            }
            int nextlen = queue.size();
            // 不是最后一行，name上一层和当前层节点数量一定是二倍关系
            if(!allNull && nextlen != 2*pre){
                return false;
            }
        }
        return true;
    }

思路2:递归方法，返回左右子树是否为满二叉树

    static class Info{
        private boolean isFull;
        private int height ;

        public Info(boolean isFull, int height) {
            this.isFull = isFull;
            this.height = height;
        }
    }

    public static boolean isFull2(Node head) {
        if(head == null)
            return true;

        Info process = process(head);
        return process.isFull;
    }
    public static Info process(Node head){
        if(head == null){
            return new Info(true,0);
        }
        Info l = process(head.left);
        Info r = process(head.right);
        boolean isFull = false;
        int height = Math.max(l.height,r.height)+1;
        if(l.isFull && r.isFull && l.height == r.height){
            isFull = true;
        }
        return new Info(isFull,height);
    }

题目：给定一棵二叉树的头节点head，返回这颗二叉树中最大的二叉搜索子树的大小

思路：递归返回子树作为根节点二叉搜索树信息、

public static class TreeNode {
		public int val;
		public TreeNode left;
		public TreeNode right;

		public TreeNode(int value) {
			val = value;
		}
	}

	// 提交如下的代码，可以直接通过
	public static int largestBSTSubtree(TreeNode head) {
		if (head == null) {
			return 0;
		}
		return process(head).maxBSTSubtreeSize;
	}

	public static class Info {
		public int maxBSTSubtreeSize;
		public int allSize;
		public int max;
		public int min;

		public Info(int m, int a, int ma, int mi) {
			maxBSTSubtreeSize = m;
			allSize = a;
			max = ma;
			min = mi;
		}
	}

	public static Info process(TreeNode x) {
		if (x == null) {
			return null;
		}
		Info leftInfo = process(x.left);
		Info rightInfo = process(x.right);
		int max = x.val;
		int min = x.val;
		int allSize = 1;
		if (leftInfo != null) {
			max = Math.max(leftInfo.max, max);
			min = Math.min(leftInfo.min, min);
			allSize += leftInfo.allSize;
		}
		if (rightInfo != null) {
			max = Math.max(rightInfo.max, max);
			min = Math.min(rightInfo.min, min);
			allSize += rightInfo.allSize;
		}
		int p1 = -1;
		if (leftInfo != null) {
			p1 = leftInfo.maxBSTSubtreeSize;
		}
		int p2 = -1;
		if (rightInfo != null) {
			p2 = rightInfo.maxBSTSubtreeSize;
		}
		int p3 = -1;
		boolean leftBST = leftInfo == null ? true : (leftInfo.maxBSTSubtreeSize == leftInfo.allSize);
		boolean rightBST = rightInfo == null ? true : (rightInfo.maxBSTSubtreeSize == rightInfo.allSize);
		if (leftBST && rightBST) {
			boolean leftMaxLessX = leftInfo == null ? true : (leftInfo.max < x.val);
			boolean rightMinMoreX = rightInfo == null ? true : (x.val < rightInfo.min);
			if (leftMaxLessX && rightMinMoreX) {
				int leftSize = leftInfo == null ? 0 : leftInfo.allSize;
				int rightSize = rightInfo == null ? 0 : rightInfo.allSize;
				p3 = leftSize + rightSize + 1;
			}
		}
		return new Info(Math.max(p1, Math.max(p2, p3)), allSize, max, min);
	}

题目：给定一棵二叉树的头节点head，任何两个节点之间都存在距离，
返回整棵二叉树的最大距离

思路：递归方法，最大宽度，要么经过当前节点，要么是左右子树任意一个最长路径

public static Info process(Node head){
        if(head == null){
            return null;
        }
        Info left = process(head.left);
        Info right = process(head.right);
        // 最大宽度经过当前head节点
        int has = 1;
        int maxwide = 0;
        int depth = 0;
        if(left != null){
            has += left.maxdepth;
            maxwide = Math.max(left.maxwide,maxwide);
            depth = Math.max(depth,left.maxdepth);
        }
        if(right != null){
            has += right.maxdepth;
            maxwide = Math.max(right.maxwide,maxwide);
            depth = Math.max(depth,right.maxdepth);
        }
        // 最大宽度要么经过当前节点，要么在左右任意子树
        maxwide = Math.max(has,maxwide);
        return new Info(depth+1,maxwide);
    }
    static class Info{
        // 最大深度
        private int maxdepth;
        // 最大宽度
        private int maxwide;

        public Info(int maxdepth, int maxwide) {
            this.maxdepth = maxdepth;
            this.maxwide = maxwide;
        }
    }

问题：给定字符串数组，返回所有组合中字典排序最小的组合对应的字符串

思路：1 暴力方法，获取所有排列组合，然后取字典排序最小的

// process 拿到所有的排列租户，然后找到最小的一个并返回
    public static String lowestString1(String[] strs) {
        // PC
        if (strs == null || strs.length <= 0) return "";

        TreeSet<String> process = process(strs);
        return process.size() == 0 ? "" : process.first();
    }

    // 返回当前数组 arrs 的所有组合
    public static TreeSet<String> process(String[] arrs) {
        TreeSet<String> ans = new TreeSet<>();
        if (arrs == null || arrs.length <= 0) {
            ans.add("");
            return ans;
        }

        for (int i = 0; i < arrs.length; i++) {
            String[] strings = removeIndex(arrs, i);
            TreeSet<String> process = process(strings);
            for (String string : process) {
                ans.add(arrs[i] + string);
            }
        }
        return ans;
    }

    public static String[] removeIndex(String[] arrs, int index) {
        int N = arrs.length;
        String[] ans = new String[N-1];
        int j = 0;
        for (int i = 0; i < arrs.length; i++) {
            if (i == index) continue;
            ans[j++] = arrs[i];
        }
        return ans;
    }

方法2 ：贪心算法，维护优先队列，将目标字符串元素加入队列，最终的队列即使字典排序最小的组合。优先队列指定比较器

public static String lowestString2(String[] strs) {
        if (strs == null || strs.length == 0) return "";
        // 1 优先队列 将元素依次放入
        Arrays.sort(strs,new Comparator<String>() {
            @Override
            public int compare(String o1, String o2) {
                return (o1 + o2).compareTo(o2 + o1);
            }
        });

        // 2 最终的队列就是结果
        StringBuilder sb = new StringBuilder();
        for (String str : strs) {
            sb.append(str);
        }
        return sb.toString();
    }

需要注意的是：往队列塞入元素时候，如果在比较i位置元素时候就确定大小顺序，i之前的所有元素是不会进行比较的,所以这里存在一个问题，咋判断当前插入元素和i之前的元素组合就不是最小的。论证如下文章来源地址https://www.toymoban.com/news/detail-831472.html

递推法
队列初始有两个字符串 a  b  并且 ab 字典序小于 ba ，所以a排在b前面
当前字符串c需要进入队列，和b进行比较，字典序大于b所以排在b后面，
比较a 和 c的字典序
字符串ac可以转换为 N(a)*M(c)+N(c) K进制的数字， 其中M(c): Math.sqrt(K,c.length) N(a) 为字符串a对应的K进制数字
字符串ca可以转换为 N(c)*M(a)+N(a)
现在需要求  N(c)*M(a)+N(a) <  N(a)*M(c)+N(c) 
已知：
ab<ba
N(a)*M(b)+N(b) < N(b)*M(a)+N(a)  公式1
bc<cb
N(b)*M(c)+N(c) < N(c)*M(b)+N(b)  公式2 

公式1 两边同时减去 N(b) 后同时乘 N(c) 因为数字不为负数所以不改变比较符号
N(a)*M(b)*N(c) < N(c)*N(b)*M(a) + N(a)*N(c) - N(b)*N(c)    公式3
公式2 两边同时减去 N(b) 后同时乘 N(a) 因为数字不为负数所以不改变比较符号
N(b)*M(c)*N(a) +N(c)*N(a)-N(b)*N(a) < N(c)*M(b)*N(a)    	公式4
公式3 左边等于公式4右边 整理得
N(b)*M(c)*N(a) +N(c)*N(a)-N(b)*N(a) < N(c)*N(b)*M(a) + N(a)*N(c) - N(b)*N(c) 
N(b)*M(c)*N(a)-N(b)*N(a) < N(c)*N(b)*M(a)- N(b)*N(c) 
M(c)*N(a) -N(a) < N(c)*M(a) -N(c) 
M(c)*N(a) +N(c) < N(c)*M(a) +N(a) 
最终得
ac<ca
所以得到结论，ab<ba 并且 bc<cb 那么 ac 一定小于 ca

如果队列前面有n个已排序字符串 现在往里面塞 字符串 s，并且 arr[n-1]+s < s+arr[n-1] 
那么可以得到 [0,n-1) 和字符串 s 存在这样的关系 Str(0,n-2)+s < s+ Str(0,n-2) 
其中Str(0,n-2) 为[0,n-2] 范围任意长度字符串组合

最终得到结论，按照代码Comparator方式插入队列后，最终的队列就是字典序最小的组合

到了这里，关于算法-二叉树相关的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！