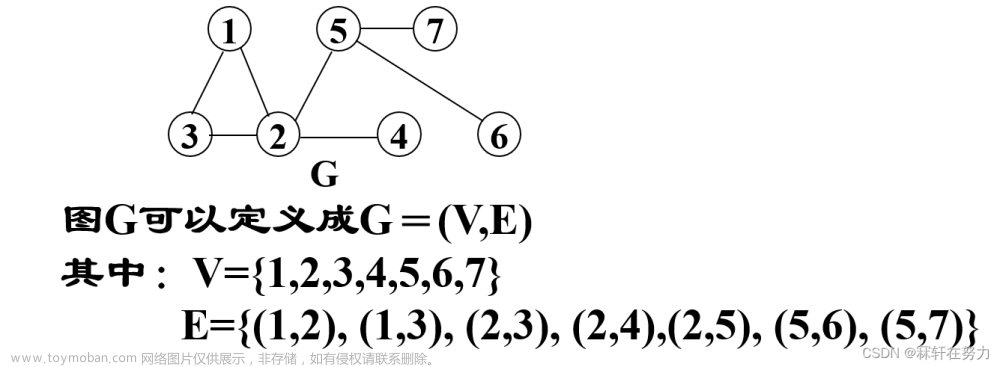
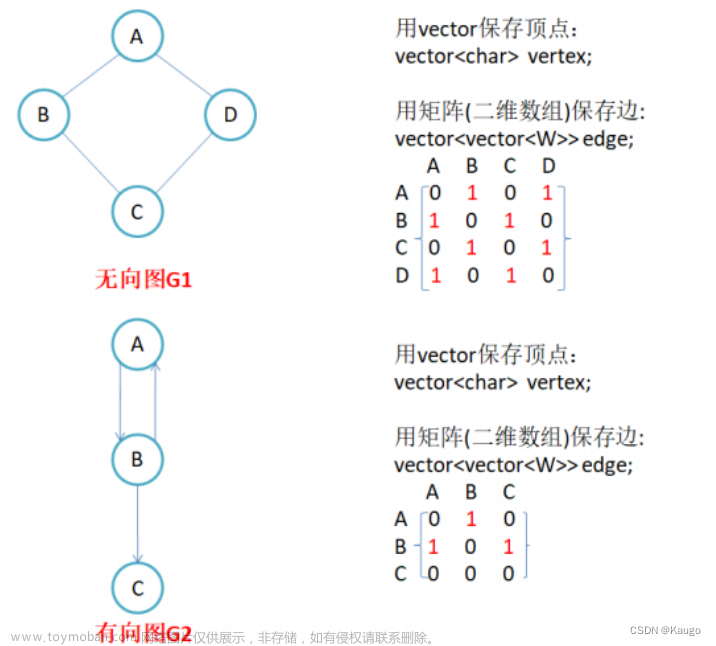
算法的重要性不言而喻,现在我们的生活也已经离不开各种算法,一个好的算法能大大提高程序的运行效率,是学习编程的一个重要模块,而遍历算法也是算法里的一个大的模块,今天我们一起来学习一下深度遍历算法(depth first search)和 广度优先遍历(broad first search)。我们通过几道经典的分析例题来理解这两种算法。

提示:以下是本篇文章正文内容,下面案例可供参考
一、宽度遍历搜索(bfs)
1.概念和算法思想
宽度优先搜索算法(又称广度优先搜索)是最简便的图的搜索算法之一,这一算法也是很多重要的图的算法的原型。Dijkstra单源最短路径算法和Prim最小生成树算法都采用了和宽度优先搜索类似的思想。其别名又叫BFS,属于一种盲目搜寻法,目的是系统地展开并检查图中的所有节点,以找寻结果。换句话说,它并不考虑结果的可能位置,彻底地搜索整张图,直到找到结果为止。
2.红与黑(牛客网)
2.1题目链接红与黑
2.2分析题面

题意:输入对应的两个数m,和n,m是行, n是列,输入一个char类型的图,遍历这个图,找到‘@‘这个点,并且从’@‘点开始计算能走到的’.'字符的总个数。
算法分析:flood fill (大水漫灌算法)
bfs算法适合做最短路的问题,遍历顺序,从’@'这个点往上右下左四个方向去搜索,所以我们可以设置两个方向数组,就可以实现。bfs的实现还要依靠队列来完成,一般是默认是STL库里提供的队列就可以了。
这道题的实现思路:
代码示例:
#include<iostream>
#include<queue>
#include<algorithm>
using namespace std;
typedef pair<int, int> pii;
#define x first //这样子代码会比较短
#define y second
const int N = 25;
char g[N][N]; //存地图
int st[N][N];
int m, n; //m是列, n是行
int bfs(int sx, int sy)
{
queue<pii> q; // 创造一个pii类型的队列,因为是二维数组
q.push({sx, sy});
st[sx][sy] = '#';// 标记为为障碍物
int res = 0; //计算总共能走的数有多少
int dx[4] = {-1, 0, 1, 0}, dy[4] = {0, 1, 0, -1};
while(q.size())
{
auto t = q.front();
q.pop();
res++;
for(int i = 0; i < 4; i++)
{
int a = t.x + dx[i], b = t.y + dy[i]; //这个是新的点
if(a < 0 || a >= n || b < 0 || b >= m || g[a][b] != '.' ) continue;
g[a][b] ='#';
q.push({a, b});
}
}
return res;
}
int main ()
{
while(cin >> m >> n, n || m)
{
for(int i = 0; i < n; i++) cin >> g[i]; //这样就把二维数组存进来了
int a, b;
for(int i = 0; i < n; i++)
for(int j = 0; j < m; j ++)
if(g[i][j] == '@') //找到@这个点的下标
{
a = i;
b = j;
}
cout << bfs(a, b) << endl;
}
return 0;
}
3.走迷宫(牛客网)
3.1题目链接走迷宫
3.2分析题面
题意:入口固定在第一行第二列,出口固定在最后一行第九列,其中’#‘代表墙, '.'代表通路,算从入口到出口的最少步数u,就相当于是最短路,也能用bfs解。
算法分析:flood fill (大水漫灌算法)
解法与上题基本没区别,但是要注意bfs函数的实现。

代码示例:
#include<iostream>
#include<queue>
#include<cstring>
#include<algorithm>
using namespace std;
typedef pair<int, int> PII;
#define x first
#define y second
const int N = 11;
char g[N][N]; //存图
int d[N][N]; //存路径
int dx[4] = {-1, 0, 1, 0}, dy[4] = {0, 1, 0 ,-1};
int bfs()
{
queue<PII> q;
memset(d, -1, sizeof d);
d[0][1] = 0;
q.push({0, 1});
while(q.size())
{
auto t = q.front();//取对头
q.pop();
for(int i = 0; i < 4; i++)
{
int a = t.x + dx[i], b = t.y + dy[i];
if(a >= 0 && a < 10 && b < 10 && b >= 0 && g[a][b] == '.' && d[a][b] == -1)
{
d[a][b] = d[t.x][t.y] + 1;
q.push({a, b});
}
}
}
return d[9][8];
}
int main ()
{
while(cin >> g[0][0])
{
for(int i = 0; i < 10; i++)
{
for(int j = 0; j < 10; j++)
{
if(i == 0 && j == 0) continue;
cin >> g[i][j];
}
}
cout << bfs() << endl;
}
return 0;
}
二、深度搜索搜索(dfs)
1.概念和算法思想
概念:事实上,深度优先搜索属于图算法的一种,英文缩写为DFS即Depth First Search.其过程简要来说是对每一个可能的分支路径深入到不能再深入为止,而且每个节点只能访问一次。
算法思想:
深度优先遍历图的方法是,从图中某顶点v出发:
(1)访问顶点v;
(2)依次从v的未被访问的邻接点出发,对图进行深度优先遍历;直至图中和v有路径相通的顶点都被访问;
(3)若此时图中尚有顶点未被访问,则从一个未被访问的顶点出发,重新进行深度优先遍历,直到图中所有顶点均被访问过为止。 当然,当人们刚刚掌握深度优先搜索的时候常常用它来走迷宫.事实上我们还有别的方法,那就是广度优先搜索(BFS).
2.排列数字(acwing)
2.1分析题面
给定一个整数n,给出1 - n的全排列。
算法分析: dfs算法,顺序很重要
代码示例:
#include<algorithm>
#include<iostream>
using namespace std;
const int N = 10;
int p[N]; //存每一次的数
bool st[N]; //标记是否走过
int n; //n设置为全局会更好
int dfs(int u)
{
if(u == n) //如果u的大小等于n,此时就可以输出p数组
{
for(int i = 0; i < n; i++) printf("%d ", p[i]);
puts("");
}
for(int i = 1; i <= n; i++)
{
if(!st[i])//如果i这个点没有被标记过,就可以进来
{
p[u] = i; //p[u] 这个点i
st[i] = true; //标记
dfs(u + 1); //继续往深处递归
st[i] = false; //恢复现场
}
}
}
int main ()
{
cin >> n;
dfs(0);
return 0;
}
3.红与黑(牛客网)(dfs)
3.1分析题面

题意: 输入对应的两个数m,和n,m是行, n是列,输入一个char类型的图,遍历这个图,找到‘@‘这个点,并且从’@‘点开始计算能走到的’.'字符的总个数。
3.2算法分析
代码示例:文章来源:https://www.toymoban.com/news/detail-831624.html
#include<iostream>
using namespace std;
const int N = 25;
int n, m;
char g[N][N];
int dx[4] = {-1, 0, 1, 0}, dy[4] = {0, 1, 0, -1};//枚举四个方向
int dfs(int x, int y)
{
int res = 1;
g[x][y] = '#';//表示这个点已经走过了
for(int i = 0; i < 4; i++)
{
int a = x + dx[i], b = y + dy[i];
if(a < 0 || a >= n || b < 0 || b >= m || g[a][b] == '#') continue;//枚举边界条件
res += dfs(a, b);
}
return res;
}
int main ()
{
while(cin >> m >> n, n || m)
{
for(int i = 0; i < n; i++) cin >> g[i];
int x, y;
for(int i = 0; i < n; i++)
for(int j = 0; j < m; j++)
if(g[i][j] == '@')
{
x = i;
y = j;
}
cout << dfs(x, y) << endl;
}
return 0;
}
4、n皇后问题
4.1分析题面

n个皇后放在n x n的国际象棋上,就是每一行要放一个皇后,但是任意一个皇后不能处在同一行和同一列和同一斜线上。
4.2算法分析(dfs)
使用类似全排列的方式,把符合条件的选出来。
代码示例:
#include<iostream>
#include<algorithm>
using namespace std;
const int N = 20;
char g[N][N];//存图
bool col[N], zx[N], yx[N];//col代表行, zx代表左斜线。yx代表右斜线
int n;
void dfs(int u)
{
if(n == u)//如果n == u表示此时g数组里已经有结果了
{
for(int i = 0; i < n; i++) puts(g[i]);
puts("");
return;
}
for(int i = 0; i < n; i++)
{
if(!col[i] && !zx[u + i] && !yx[n - u + i])//如果行,左斜线,右斜线都没被标记过
{
g[u][i] = 'Q';
col[i] = zx[u + i] = yx[n - u + i] = true;
dfs(u + 1);
col[i] = zx[u + i] = yx[n - u + i] = false;
g[u][i] = '.'; //恢复现场
}
}
}
int main ()
{
cin >> n;
for(int i = 0; i < n; i++)
for(int j = 0; j < n; j++)
g[i][j] = '.';
dfs(0);
return 0;
}
三、总结

本文总结了几道bfs和dfs的经典例题, 比如红与黑这道题,我们用dfs和bfs两种方法去解决,算法是一个重要的学习模块,需要我们多刷题和总结,希望大家读后能够有所收获!!!文章来源地址https://www.toymoban.com/news/detail-831624.html
到了这里,关于【算法手札】深入理解宽度遍历(bfs)和深度遍历(dfs)搜索的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!