算法设计与分析实验：DFS与BFS

目录

一、边界着色

1.1 思路一：DFS

1.2 思路二：BFS

二、课程表II

2.1 思路一：DFS

2.2 思路二：拓扑排序

三、岛屿的最大面积

3.1 具体思路

3.2 思路展示

3.3 代码实现

3.4 复杂度分析

3.5 运行结果

2024-1-31 阴

一、边界着色

力扣第1034题

1.1 思路一：DFS

（1）具体思路：

首先，定义一个dfs函数，用于搜索和染色连通分量的边界。

在dfs函数中，首先判断当前位置是否越界或者颜色已经被染过，如果是，则返回。

将当前位置的颜色改为目标颜色color。

递归调用dfs函数，分别对当前位置的上、下、左、右四个方向进行搜索。

在dfs函数外部，首先获取起始位置grid[row][col]的颜色origin_color。

调用dfs函数，从起始位置开始进行搜索。

返回最终的网格grid。

（2）算法思路展示

以给定示例grid = [[1,2,2],[2,3,2]], row = 0, col = 1, color = 3为例

原始网格:

1  2  2  

2  3  2  

以(0,1)位置开始染色:

1  3  3  

2  3  2  

在这个图中，首先我们从起始位置(0,1)开始进行搜索。搜索过程中，我们递归地访问每个与当前位置相邻且颜色相同的位置，并将其颜色改为目标颜色3。因此，我们在递归搜索的过程中，会将位置(0,1)周围的两个位置(0,0)和(1,1)的颜色都染成3。

注意，我们只染色连通分量的边界，而不是连通分量内部的所有位置。在这个例子中，原本的连通分量是由四个位置组成的，即(0,1), (1,1), (1,2), (0,2)。但我们只需要染色该连通分量的边界，所以最终只有(0,0)和(0,2)两个位置被染成了3。

（3）代码实现

def dfs(grid, row, col, color, origin_color):
    if row < 0 or row >= len(grid) or col < 0 or col >= len(grid[0]) or grid[row][col] != origin_color:
        return

    grid[row][col] = color

    dfs(grid, row - 1, col, color, origin_color)  # 上
    dfs(grid, row + 1, col, color, origin_color)  # 下
    dfs(grid, row, col - 1, color, origin_color)  # 左
    dfs(grid, row, col + 1, color, origin_color)  # 右


def colorBorder(grid, row, col, color):
    origin_color = grid[row][col]
    dfs(grid, row, col, color, origin_color)
    return grid


grid = [[1,2,2],[2,3,2]]
row = 0
col = 1
color = 3
result = colorBorder(grid, row, col, color)
print(result)

（4）复杂度分析

DFS算法的时间复杂度为O(m*n)，其中m和n分别为网格的行数和列数。这是因为在最坏情况下，我们需要遍历所有的位置，每个位置只会被访问一次。

空间复杂度为O(mn)，其中m和n分别为网格的行数和列数。这是因为DFS算法的递归调用会使用到系统栈空间，最坏情况下，递归调用的深度为mn。

综上所述，DFS算法的时间复杂度为O(mn)，空间复杂度为O(mn)。

1.2 思路二：BFS

（1）具体思路

首先，我们需要创建一个大小为m x n的数组visited，用于记录每个节点是否被访问过。同时，我们也需要定义目标颜色color和当前位置的起始颜色origin_color（即grid[row][col]的颜色）。

接着，我们将起始位置grid[row][col]的颜色改为目标颜色color，并将其坐标(row, col)加入队列queue中。

对于队列中的每个节点，我们将其四周的相邻节点加入队列中，并检查它们是否应该被染色。如果一个相邻节点与起始位置(grid[row][col])颜色相同且未被访问过，则将其颜色改为目标颜色color，并将其坐标加入队列中。

当队列为空时，所有与起始位置(grid[row][col])相连通的节点都被遍历过了，我们就可以返回最终的网格grid。

（2）算法思路展示

初始网格 (grid)：

1 1

1 2

起始位置 (row, col) = (0, 0)

目标颜色 (color) = 3

将起始位置染色后的网格 (grid)：

3 3

1 2

队列 (queue)：(0, 0)

开始遍历与起始位置相连通的节点：

访问节点 (0, 0)，颜色为 3，添加其相邻节点到队列：

队列 (queue)：(1, 0), (0, 1)

遍历队列中的节点：

访问节点 (1, 0)，颜色为 1，与起始位置颜色不同，不需要染色，继续遍历队列中的节点

访问节点 (0, 1)，颜色为 3，已经染色，不需要再次染色，继续遍历队列中的节点

队列为空，所有与起始位置相连通的节点都已经遍历过，最终的网格为：

3 3

3 2

（3）代码实现

# BFS
def colorBorder(grid, row, col, color):
    m, n = len(grid), len(grid[0])
    visited = [[False] * n for _ in range(m)]
    origin_color = grid[row][col]

    queue = [(row, col)]
    visited[row][col] = True
    grid[row][col] = color

    while queue:
        r, c = queue.pop(0)

        for nr, nc in [(r + 1, c), (r - 1, c), (r, c + 1), (r, c - 1)]:
            if 0 <= nr < m and 0 <= nc < n and not visited[nr][nc]:
                if grid[nr][nc] == origin_color:
                    queue.append((nr, nc))
                    visited[nr][nc] = True
                    grid[nr][nc] = color
                else:
                    grid[r][c] = color

    return grid

（4）运行结果

以示例2为例，输入输出如下

输入：grid = [[1,2,2],[2,3,2]], row = 0, col = 1, color = 3

输出：[[1,3,3],[2,3,3]]

输出与预期一致

二、课程表II

力扣第210题

2.1 思路一：DFS

（1）具体思路

我们可以将每门课程看作图中的一个节点，prerequisites中的每对 [ai, bi] 则表示一条从节点 bi 指向节点 ai 的有向边。

首先，我们需要创建一个邻接表来表示图的结构。然后，我们从每个节点开始进行DFS遍历，遍历过程中使用一个visited数组来记录每个节点的访问状态。

详细过程即创建一个邻接表，使用一个列表来表示图的结构，列表的索引表示节点编号，每个索引对应的值是一个列表，其中包含所有指向该节点的节点。

创建一个visited数组，用于记录每个节点的访问状态。初始时，所有节点的访问状态都设置为0（未访问）。

对于每个节点 i，如果它的访问状态为0（未访问），则调用DFS函数进行深度优先搜索。

在DFS函数中，首先将当前节点的访问状态设置为1（正在访问）。

然后，遍历当前节点的所有邻居节点（通过邻接表获取），如果某个邻居节点的访问状态为1（正在访问），说明存在环，无法完成所有课程的学习，返回空数组。

如果邻居节点的访问状态为0（未访问），则继续以邻居节点为起点进行DFS遍历。

当遍历完当前节点的所有邻居节点后，将当前节点的访问状态设置为2（已完成访问），并将当前节点加入结果数组的末尾。

最后，返回结果数组的逆序，即为一种可行的课程学习顺序。

（2）算法思路展示

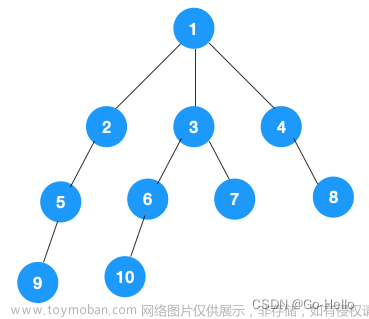
假设有4门课程。

它们之间的依赖关系如下所示；         则对应的图结构如下所示：

其中，每个节点的编号表示对应的课程编号，列表中的数字表示该节点的所有邻居节点。例如，节点1表示课程1，它有两个邻居节点2和3，表示必须先学习完课程2和课程3才能开始学习课程1。

按照DFS思路，从节点0（即课程0）开始DFS，访问过程如下所示：

访问节点0，将其标记为已访问。

访问节点1，将其标记为正在访问。

访问节点2，将其标记为正在访问。

访问节点4，将其标记为已访问，并将其加入结果数组的末尾。

返回节点2，将其标记为已访问，并将其加入结果数组的末尾。

访问节点3，将其标记为正在访问。

访问节点4，但由于节点4已经被访问过了，因此直接返回。

返回节点3，将其标记为已访问，并将其加入结果数组的末尾。

返回节点1，将其标记为已访问，并将其加入结果数组的末尾。

返回节点0，结束访问过程。

因此，这个图的一种可行的课程学习顺序为：4 -> 2 -> 3 -> 1 -> 0。

（3）代码实现

#DFS
def findOrder(numCourses, prerequisites):
    # 创建邻接表
    graph = [[] for _ in range(numCourses)]
    for pair in prerequisites:
        ai, bi = pair
        graph[bi].append(ai)

    # 记录每个节点的访问状态
    visited = [0] * numCourses

    # 用于记录结果的数组
    result = []

    # DFS遍历
    def dfs(node):
        # 访问状态设置为1（正在访问）
        visited[node] = 1

        # 遍历当前节点的邻居节点
        for neighbor in graph[node]:
            # 如果邻居节点正在被访问，则存在环，返回空数组
            if visited[neighbor] == 1:
                return False
            # 如果邻居节点未被访问，则以邻居节点为起点进行DFS遍历
            elif visited[neighbor] == 0:
                if not dfs(neighbor):
                    return False

        # 遍历完所有邻居节点后，将当前节点的访问状态设置为2（已完成访问）
        visited[node] = 2
        # 将当前节点加入结果数组的末尾
        result.append(node)

        return True

    # 对每个未访问过的节点进行DFS遍历
    for node in range(numCourses):
        if visited[node] == 0:
            if not dfs(node):
                return []

    # 返回结果数组的逆序
    return result[::-1]


numCourses = 4
prerequisites = [[1,0],[2,0],[3,1],[3,2]]
print(findOrder(numCourses, prerequisites)) # [0, 1, 2, 3] 或 [0, 2, 1, 3]

（4）复杂度分析

I时间复杂度分析：

创建邻接表的过程需要遍历 prerequisites 列表，时间复杂度为 O(E)，其中 E 是 prerequisites 的长度。

DFS 遍历的过程中，每个节点只会被访问一次，同时每条边也只会被遍历一次。因此，DFS 的时间复杂度为 O(V+E)，其中 V 是课程数量（numCourses），E 是 prerequisites 的长度。

综合起来，整个算法的时间复杂度为 O(V+E)。

II空间复杂度分析：

创建邻接表需要额外的空间来存储图的结构，所以空间复杂度为 O(V+E)。

visited 数组和 result 数组的大小都为 numCourses，所以额外的空间复杂度为 O(V)。

综合起来，整个算法的空间复杂度为 O(V+E)。

我认为需要注意的是，这里的 V 和 E 分别代表课程数量和 prerequisites 的长度，并不考虑具体图的结构。

2.2 思路二：拓扑排序

（1）具体思路

拓扑排序是一种基于有向无环图（DAG）的算法，用于将图中所有节点排序，使得所有的有向边均从排在前面的元素指向排在后面的元素。我们可以将每门课程看作一个节点，每个先修课程关系看作一条有向边，然后使用拓扑排序求解即可。

具体实现过程如下：

初始化每个节点的入度数组 indegrees 和邻接表 graph。其中，indegrees[i] 表示节点 i 的入度，graph[i] 存储以节点 i 为起点的所有边的终点。

遍历 prerequisites 数组，根据先修课程关系更新每个节点的入度和邻接表。

将入度为 0 的节点加入队列 queue 中。

当队列不为空时，取出队首节点 node，并且遍历 node 的邻接表，将每个邻接节点的入度减 1。如果邻接节点的入度变为 0，则把它加入队列 queue 中。

重复步骤 4 直到队列为空。如果存在入度不为 0 的节点，说明存在环，无法完成所有课程的学习，返回空数组。否则，返回拓扑排序的结果。

（2）算法思路展示

假设有 4 门课程：A、B、C、D。根据先修课程关系，我们可以得到以下简图：

A --> B --> C --> D

下面将逐步演示拓扑排序的过程：

初始化入度数组和邻接表：

入度数组：A: 0, B: 1, C: 2, D: 1

邻接表：

A: B, C

B: C

C: D

D:

将入度为 0 的节点加入队列：

初始时，队列中只有节点 A。

开始拓扑排序循环：

取出队首节点 A。

遍历节点 A 的邻接表，即 B 和 C。

对于节点 B，将其入度减 1，变为 0。

对于节点 C，将其入度减 1，变为 1。

队列中现在有节点 B。

继续拓扑排序循环：

取出队首节点 B。

遍历节点 B 的邻接表，即 C。

对于节点 C，将其入度减 1，变为 0。

队列中现在有节点 C。

继续拓扑排序循环：

取出队首节点 C。

遍历节点 C 的邻接表，即 D。

对于节点 D，将其入度减 1，变为 0。

队列中现在有节点 D。

继续拓扑排序循环：

取出队首节点 D。

遍历节点 D 的邻接表，没有邻接节点。

拓扑排序完成，所有节点都已被排序。

最终的拓扑排序结果为 A、B、C、D。

（3）代码实现

class Solution:
    def findOrder(self, numCourses: int, prerequisites: List[List[int]]) -> List[int]:
        # 初始化每个节点的入度数组 indegrees 和邻接表 graph
        indegrees = [0] * numCourses
        graph = [[] for _ in range(numCourses)]
        
        # 遍历 prerequisites 数组，根据先修课程关系更新每个节点的入度和邻接表
        for cur, pre in prerequisites:
            indegrees[cur] += 1
            graph[pre].append(cur)
        
        # 将入度为 0 的节点加入队列 queue 中
        queue = collections.deque([i for i in range(numCourses) if indegrees[i] == 0])
        res = []
        
        # 拓扑排序
        while queue:
            node = queue.popleft()
            res.append(node)
            for neighbor in graph[node]:
                indegrees[neighbor] -= 1
                if indegrees[neighbor] == 0:
                    queue.append(neighbor)
        
        # 如果存在入度不为 0 的节点，说明存在环，无法完成所有课程的学习
        if len(res) != numCourses:
            return []
        else:
            return res

（4）运行结果

示例 1：

输入：numCourses = 2, prerequisites = [[1,0]]

输出：[0,1]

示例 2：

输入：numCourses = 4, prerequisites = [[1,0],[2,0],[3,1],[3,2]]

输出：[0,2,1,3]

观察结果可知输出与预期一致

三、岛屿的最大面积

力扣第695题

本题采用DFS的思想求解

3.1 具体思路

可以遍历矩阵中的每个单元格，并对每个单元格执行 DFS 操作来找到相邻的岛屿单元格，并计算岛屿的面积。在 DFS 过程中，需要标记已经访问过的单元格，以防止重复计数。

下面是详细的思路和代码：

定义一个函数 dfs，用于执行深度优先搜索。参数包括当前单元格的行索引、列索引、矩阵的行数、列数以及矩阵本身。

在 dfs 函数中，首先判断当前单元格是否越界或者已经访问过。如果是，则返回 0

然后将当前单元格标记为已访问。

初始化岛屿面积为 1，表示当前单元格包含在岛屿中。

分别向上、下、左、右四个方向进行递归调用 dfs，并将结果累加到岛屿面积中。

最后返回岛屿面积。

主函数中，首先获取矩阵的行数和列数，然后初始化最大岛屿面积为 0。

遍历矩阵中的每个单元格，如果遇到值为 1 的单元格，则执行 DFS 操作，并更新最大岛屿面积。

返回最大岛屿面积作为结果。

3.2 思路展示

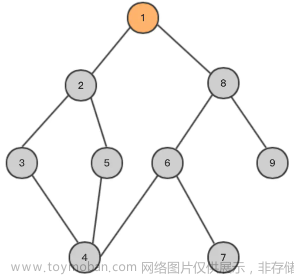
当矩阵为如下所示时：

我们可以用如下的图示来表示每个单元格的相邻关系：

其中，1 表示岛屿，0 表示海洋。可以看出相邻的岛屿单元格是上、下、左、右四个方向相邻的单元格。

我们可以按照上述思路使用深度优先搜索来计算岛屿的面积。以矩阵中第一个岛屿为例，即从左上角的位置(0, 0) 开始进行深度优先搜索。

首先，将位置 (0, 0) 标记为已访问，并初始化岛屿面积为 1。然后，尝试向上、向下、向左、向右四个方向进行递归调用 dfs 函数。在这个例子中，只能向右和向下移动。

向右移动到位置 (0, 1)，发现是海洋，终止递归。向下移动到位置 (1, 0)，发现是海洋，终止递归。

遍历完当前岛屿中的所有单元格后，得到该岛屿的面积为 1。

接下来，继续遍历矩阵中的下一个单元格，即位置 (0, 4)。该位置是岛屿，进行深度优先搜索。

向右移动到位置 (0, 3)，发现是海洋，终止递归。向下移动到位置 (1, 4)，发现是海洋，终止递归。

遍历完当前岛屿中的所有单元格后，得到该岛屿的面积为 1。

依此类推，我们可以得到所有岛屿的面积，并找到最大的岛屿面积。

3.3 代码实现

from typing import List


class Solution:
    def maxAreaOfIsland(self, grid: List[List[int]]) -> int:
        def dfs(row, col, rows, cols, grid):
            if row < 0 or row >= rows or col < 0 or col >= cols or grid[row][col] == 0:
                return 0

            grid[row][col] = 0
            area = 1
            area += dfs(row - 1, col, rows, cols, grid)
            area += dfs(row + 1, col, rows, cols, grid)
            area += dfs(row, col - 1, rows, cols, grid)
            area += dfs(row, col + 1, rows, cols, grid)

            return area

        rows = len(grid)
        cols = len(grid[0])
        max_area = 0

        for i in range(rows):
            for j in range(cols):
                if grid[i][j] == 1:
                    max_area = max(max_area, dfs(i, j, rows, cols, grid))

        return max_area
# 示例测试代码
solution = Solution()
grid1 = [[0,0,1,0,0,0,0,1,0,0,0,0,0],
         [0,0,0,0,0,0,0,1,1,1,0,0,0],
         [0,1,1,0,1,0,0,0,0,0,0,0,0],
         [0,1,0,0,1,1,0,0,1,0,1,0,0],
         [0,1,0,0,1,1,0,0,1,1,1,0,0],
         [0,0,0,0,0,0,0,0,0,0,1,0,0],
         [0,0,0,0,0,0,0,1,1,1,0,0,0],
         [0,0,0,0,0,0,0,1,1,0,0,0,0]]

grid2 = [[0,0,0,0,0,0,0,0]]

print(solution.maxAreaOfIsland(grid1))  # 输出：6
print(solution.maxAreaOfIsland(grid2))  # 输出：0

3.4 复杂度分析

对于给定的二维网格，假设有 m 行 n 列。

时间复杂度分析：

矩阵遍历的时间复杂度为 O(m*n)。

对于每个岛屿，进行深度优先搜索的时间复杂度取决于岛屿的大小。最坏情况下，岛屿的大小为 mn（全为陆地），此时深度优先搜索的时间复杂度为 O(mn)。

因此，总体时间复杂度为 O(mn + mn) = O(m*n)。

空间复杂度分析：

递归调用 dfs 函数的最大深度为岛屿的大小（即 m*n）。

由于每次递归调用都会创建新的堆栈帧，因此空间复杂度为 O(m*n)。

在最坏情况下，所有的位置都是陆地，岛屿的大小为 mn，所以空间复杂度为 O(mn)。

如果修改输入数组 grid，将访问过的陆地标记为 0，可以在原地完成计算，空间复杂度可以降低为 O(1)。

综上所述，算法的时间复杂度为 O(mn)，空间复杂度为 O(mn)（如果不修改输入数组，则为 O(1)）。

3.5 运行结果

示例1输入：grid = 

[[0,0,1,0,0,0,0,1,0,0,0,0,0],[0,0,0,0,0,0,0,1,1,1,0,0,0],[0,1,1,0,1,0,0,0,0,0,0,0,0],[0,1,0,0,1,1,0,0,1,0,1,0,0],[0,1,0,0,1,1,0,0,1,1,1,0,0],[0,0,0,0,0,0,0,0,0,0,1,0,0],[0,0,0,0,0,0,0,1,1,1,0,0,0],[0,0,0,0,0,0,0,1,1,0,0,0,0]]

输出：6

示例 2

输入：grid = [[0,0,0,0,0,0,0,0]]

输出：0

2024-1-31 阴

“过自己的生活 自己设立目标 完成目标 其他人 其他事 都少管 少看 少操心 精力留给自己”文章来源地址https://www.toymoban.com/news/detail-831943.html

到了这里，关于算法设计与分析实验：DFS与BFS的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！