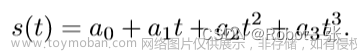伴侣矩阵求解多项式的根-Toy模板网

这篇具有很好参考价值的文章主要介绍了伴侣矩阵求解多项式的根。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

伴侣矩阵求解多项式的根

已知方程 $\sum_{i=0}^{n}a_ix^n = 0$ ，通过伴侣矩阵求解该方程的根。

伴侣矩阵

此处参考百度知道，就可以大概知道伴侣矩阵的构建。具体如下，

设
$f(t)=t^n+a_1 t^{n-1}+\ldots+a_{n-1} t+a_n .$

是数域 $F$ 上的首项为 1 的多项式, 则 $n$ 阶矩阵:
$C=\left[\begin{array}{ccccc} 0 & 0 & \ldots & 0 & -a_n \\ 1 & 0 & \ldots & 0 & -a_{n-1} \\ 0 & 1 & \ldots & 0 & -a_{n-2} \\ \vdots & \vdots & & \vdots & \vdots \\ 0 & 0 & \ldots & 1 & -a_1 \end{array}\right]$
对于原来的多项式 $a_0$ 系数可能不为1，那就可以通过左右两边同时除以 $a_0$ 得到首项系数为1的多项式。

求解示例

假设我们有一个多项式如下。
$P(x)=a_0 x^3+a_1 x^2+a_2 x+a_3=0$
令 $b_1 = \frac{a_1}{a_0}$ ， $b_2 = \frac{a_2}{a_0}$ …依此类推，就得到了如下
$P'(x)=x^3+b_1 x^2+b_2 x+b_3=0$
此时 $P^{'}$ 和 $P$ 的根是相同。构建伴侣矩阵A：
$\left[\begin{array}{lll} 0 & 0 & -b_3 \\ 1 & 0 & -b_2 \\ 0 & 1 & -b_1 \end{array}\right]$
为了便于观察，可以将A先进行转置，此时的特征根和特征方程是不会发生改变的。

令，

$\left[\begin{array}{ccc} -b_1 &- b_2 & -b_3 \\ 1 & 0 & 0 \\ 0 & 1 & 0 \end{array}\right]$

然后就求解该矩阵的特征值和特征向量，由定义得，
$A\bold{y} = \lambda \bold{y}$
我们可以假设此时多项式 $P (x)$ 的根 $x_0$ 就是矩阵 A阵的特征值，因此有
$\mathbf{y}=x_0 \mathbf{y}$
然后，令 $\mathbf{y}=\left[x_0^2, x_0, 1\right]^T$ ，就可以得到，
$A\mathbf{y} = \left[\begin{array}{ccc} -b_1x_0^2 -b_2x_0 -b_3 \\ x_0^2 \\ x_0 \end{array}\right] = \left[\begin{array}{c}x_0^3 \\ x_0^2 \\ x_0\end{array}\right] = x_0\mathbf{y}$
此时第一行就得到了我们所需要求解的方程了。

$b_1x_0^2 - b_2x_0-b_3 = x_0^3$

所以只需要解出伴侣矩阵A的所有特征根 $x_0$ 就可以求出原来方程的根了。

参考文档: 传送门

然后让GPT随机给我生成了一个示例的代码，可以验证一下，文章来源地址https://www.toymoban.com/news/detail-831984.html

import numpy as np
import sympy as sp
import matplotlib.pyplot as plt

# 定义三次方程的系数
coefficients = [1, -6, 11, -6]

# 构建友矩阵
A = [[-coefficients[1], -coefficients[2], -coefficients[3]],
     [1, 0, 0],
     [0, 1, 0]]
A = np.array(A)

# 输出友矩阵
print("Companion Matrix A:")
print(A)

# 求解特征值
eigenvalues = np.linalg.eigvals(A)

# 输出结果
print("\nCoefficients of the cubic equation:", coefficients)
print("Eigenvalues of the companion matrix:", eigenvalues)


# 求解方程的准确根
# Define the symbolic variable x
x = sp.symbols('x')

# Define the cubic equation
equation = x**3 - 6*x**2 + 11*x - 6

# Solve the cubic equation
roots = sp.solve(equation, x)

# Display the roots
print("\nExact roots of the cubic equation:", roots)

# Plot the cubic equation
def cubic_equation(x):
    return x**3 - 6*x**2 + 11*x - 6

x_values = np.linspace(0, 4, 400)
y_values = cubic_equation(x_values)

plt.plot(x_values, y_values, label='y = $x^3 - 6x^2 + 11x - 6$')
plt.axhline(0, color='black', linewidth=0.5, linestyle='--', label='y = 0')

plt.scatter(roots, [0, 0, 0], color='black', marker='o', label='Roots')

plt.xlabel('x')
plt.ylabel('y')
plt.title('Plot of the Cubic Equation')
plt.legend()
plt.grid(True)

plt.show()