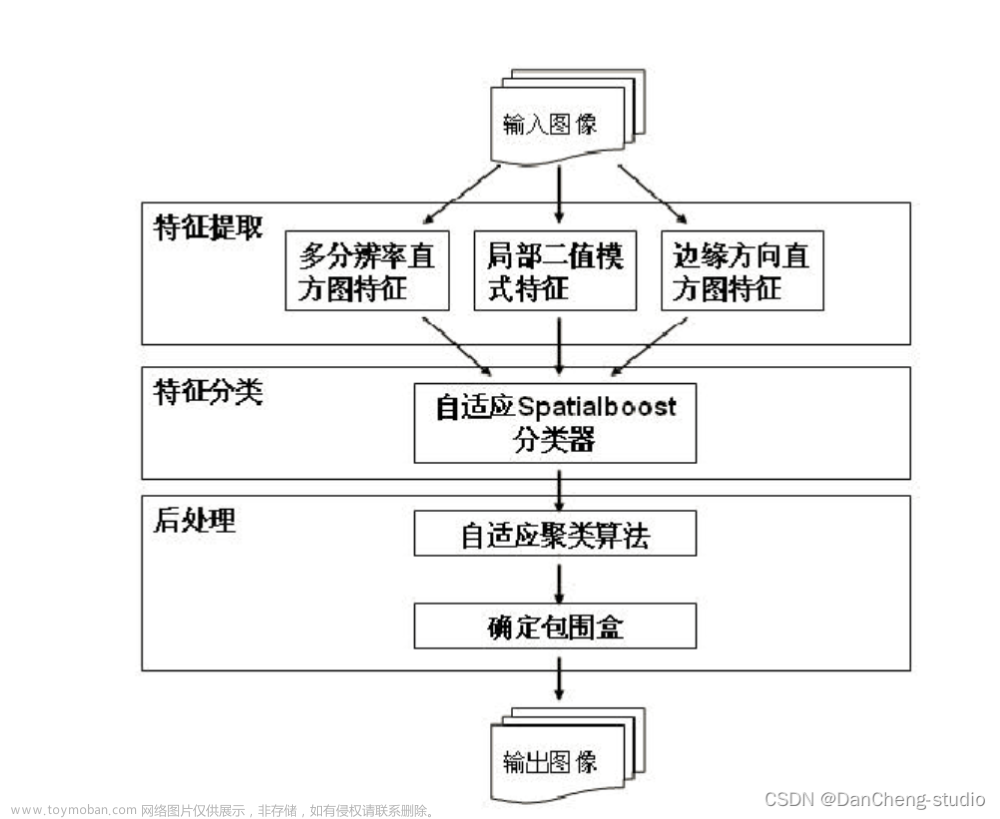
相机模型

坐标系变换
针孔相机模型存在四个坐标系:世界坐标系、摄像机坐标系、图像物理坐标系和图像像素坐标系
- 世界坐标系:绝对坐标系,物体在真实世界中的坐标系(3D)
- 摄像机坐标系:以相机的光心为坐标系的原点,以平行于图像的x和y方向为x轴和y轴, z轴和光轴平行, x,y, z互相垂直,单位是长度单位。(3D)
- 图像物理坐标系:以主光轴和图像平面交点为坐标原点, x’和y’方向如图所示,单位是长度单位(2D)
- 图像像素坐标系:以图像的顶点为坐标原点, u和v方向平行于x’和y’方向, 单位是以像素计。(2D)
从世界坐标系转换到摄像机坐标系
基础知识复习
坐标变换
摄像机在不断的运动(旋转+平移),所以摄像机的坐标系也跟随着移动,而世界坐标系是不动的,要完成世界坐标系到摄像机坐标系的转换,需要将坐标系进行旋转和平移
为了便于将平移转换为线性运算,把坐标转换到齐次坐标(用N+1维来代表N维坐标)下。
N=3,N+1=4
在二维坐标变换里,
旋转:
因为是坐标系的变换,所以旋转矩阵R(
3
∗
3
3*3
3∗3)为点旋转的逆矩阵
R
=
R
x
R
y
R
y
R =R_{x}R_{y}R_{y}
R=RxRyRy
平移:
因为是坐标系的变换,所以矩阵T(
3
∗
3
3*3
3∗3)为点平移的逆矩阵
T
=
[
1
0
0
x
0
0
1
0
y
0
0
0
1
z
0
0
0
0
1
]
T=\begin{bmatrix} 1 & 0&0 & x_{0}\\ 0& 1&0 & y_{0} \\ 0& 0 &1&z_{0} \\ 0& 0 &0&1\end{bmatrix}
T=⎣⎢⎢⎡100001000010x0y0z01⎦⎥⎥⎤
可得三维平移向量为
t
=
[
x
0
y
0
z
0
]
t=\begin{bmatrix}x0 \\ y0\\z0 \end{bmatrix}
t=⎣⎡x0y0z0⎦⎤
把平移和旋转放到一起就得到了
[
x
c
y
c
z
c
1
]
=
[
R
t
0
1
]
[
x
w
y
w
z
w
1
]
\begin{bmatrix} x_{c}\\y_{c} \\z_{c}\\1\end{bmatrix}=\begin{bmatrix} R& t\\ 0&1\end{bmatrix}\begin{bmatrix} x_{w}\\ y_{w}\\ z_{w}\\1\end{bmatrix}
⎣⎢⎢⎡xcyczc1⎦⎥⎥⎤=[R0t1]⎣⎢⎢⎡xwywzw1⎦⎥⎥⎤
其中下角标c表示相机坐标系下,w表示在世界坐标系下,R为三轴旋转矩阵,t为三维平移向量,
由此得到了世界坐标系到相机坐标系的转换
摄像头坐标系到图像物理坐标系的转换

根据图中两个三角形相似可得
f
Z
c
=
y
y
c
\frac{f}{Z_{c}} = \frac{y}{y_{c}}
Zcf=ycy
f
Z
c
=
x
x
c
\frac{f}{Z_{c}} = \frac{x}{x_{c}}
Zcf=xcx
解得
y
=
y
c
f
Z
c
y=\frac{y_{c}f}{Z_{c}}
y=Zcycf
x
=
x
c
f
Z
c
x=\frac{x_{c}f}{Z_{c}}
x=Zcxcf
划成矩阵形式,并且因为图像坐标系由三维降到了二维,z轴丢失了,要使矩阵能够相乘,需把矩阵补成
3
∗
4
3*4
3∗4
[
x
y
1
]
=
[
f
Z
c
0
0
0
0
f
Z
c
0
0
0
0
1
Z
c
0
]
[
x
c
y
c
z
c
1
]
\begin{bmatrix} x\\y \\1\end{bmatrix}=\begin{bmatrix} \frac{f}{Z_{c}} &0 & 0 &0 \\ 0& \frac{f}{ Z_{c}} & 0 & 0\\ 0& 0& \frac{1}{ Z_{c}} &0\end{bmatrix}\begin{bmatrix} x_{c}\\ y_{c}\\ z_{c}\\1\end{bmatrix}
⎣⎡xy1⎦⎤=⎣⎢⎡Zcf000Zcf000Zc1000⎦⎥⎤⎣⎢⎢⎡xcyczc1⎦⎥⎥⎤
左右同乘
Z
c
Z_{c}
Zc得:
Z
c
[
x
y
1
]
=
[
f
0
0
0
0
f
0
0
0
0
1
0
]
[
x
c
y
c
z
c
1
]
Z_{c}\begin{bmatrix} x\\y \\1\end{bmatrix}=\begin{bmatrix} f &0 & 0 &0 \\ 0& f & 0 & 0\\ 0& 0& 1 &0\end{bmatrix}\begin{bmatrix} x_{c}\\ y_{c}\\ z_{c}\\1\end{bmatrix}
Zc⎣⎡xy1⎦⎤=⎣⎡f000f0001000⎦⎤⎣⎢⎢⎡xcyczc1⎦⎥⎥⎤
由此得到了物理图像坐标系的x,y坐标,注意该x,y的单位还是为现实世界里的(米,毫米…)
同时也完成了由三维到二维的转化。
图像物理坐标系转化到图像像素坐标系

O
o
v
O_{ov}
Oov坐标系表示像素坐标系,
O
x
y
O_{xy}
Oxy表示物理坐标系,这两个坐标系之间存在缩放和平移
缩放:真实世界的坐标单位和图像里的像素存在一定的比例关系
假设一个像素对应真实世界的距离dx,dy
平移:两个坐标系原点不重合,假设图像中心在像素系的坐标为(
u
0
,
v
0
u_{0},v_{0}
u0,v0)
缩放和平移矩阵运算:坐标变换
可得出该两个坐标系之间的转换关系为:
[
u
v
1
]
=
[
1
d
x
0
u
0
0
1
d
y
v
0
0
0
1
]
[
x
y
1
]
\begin{bmatrix} u\\v \\1\end{bmatrix}=\begin{bmatrix} \frac{1}{d_{x}} &0 & u_{0} \\ 0& \frac{1}{d_{y}} & v_{0} \\ 0& 0& 1 \end{bmatrix}\begin{bmatrix} x\\ y\\1\end{bmatrix}
⎣⎡uv1⎦⎤=⎣⎡dx1000dy10u0v01⎦⎤⎣⎡xy1⎦⎤
模型总结
把上述所有变换总结在一起,得到以下关系式
Z
c
[
u
v
1
]
=
[
1
d
x
0
u
0
0
1
d
y
v
0
0
0
1
]
[
f
0
0
0
0
f
0
0
0
0
1
0
]
[
R
t
0
1
]
[
x
w
y
w
z
w
1
]
=
[
a
x
0
u
0
0
a
y
v
0
0
0
1
]
[
R
t
0
1
]
[
x
w
y
w
z
w
1
]
Z_{c}\begin{bmatrix} u\\ v\\1\end{bmatrix}=\begin{bmatrix} \frac{1}{d_{x}} &0 & u_{0} \\ 0& \frac{1}{d_{y}} & v_{0} \\ 0& 0& 1 \end{bmatrix}\begin{bmatrix} f &0 & 0 &0 \\ 0& f & 0 & 0\\ 0& 0& 1 &0\end{bmatrix}\begin{bmatrix} R& t\\ 0&1\end{bmatrix}\begin{bmatrix} x_{w}\\ y_{w}\\ z_{w}\\1\end{bmatrix}=\begin{bmatrix} a_{x} &0 & u_{0} \\ 0& a_{y} & v_{0} \\ 0& 0& 1 \end{bmatrix}\begin{bmatrix} R& t\\ 0&1\end{bmatrix}\begin{bmatrix} x_{w}\\ y_{w}\\ z_{w}\\1\end{bmatrix}
Zc⎣⎡uv1⎦⎤=⎣⎡dx1000dy10u0v01⎦⎤⎣⎡f000f0001000⎦⎤[R0t1]⎣⎢⎢⎡xwywzw1⎦⎥⎥⎤=⎣⎡ax000ay0u0v01⎦⎤[R0t1]⎣⎢⎢⎡xwywzw1⎦⎥⎥⎤
其中
a
x
=
f
/
d
x
a_{x}=f/d_{x}
ax=f/dx ,
a
x
=
f
/
d
y
a_{x}=f/d_{y}
ax=f/dy 都是常数,所以把他化为一个
其中矩阵
[
1
d
x
0
u
0
0
1
d
y
v
0
0
0
1
]
\begin{bmatrix} \frac{1}{d_{x}} &0 & u_{0} \\ 0& \frac{1}{d_{y}} & v_{0} \\ 0& 0& 1 \end{bmatrix}
⎣⎡dx1000dy10u0v01⎦⎤和矩阵
[
f
0
0
0
0
f
0
0
0
0
1
0
]
\begin{bmatrix} f &0 & 0 &0 \\ 0& f & 0 & 0\\ 0& 0& 1 &0\end{bmatrix}
⎣⎡f000f0001000⎦⎤只和相机本身有关,他们相乘等于矩阵
[
a
x
0
u
0
0
a
y
v
0
0
0
1
]
\begin{bmatrix} a_{x} &0 & u_{0} \\ 0& a_{y} & v_{0} \\ 0& 0& 1 \end{bmatrix}
⎣⎡ax000ay0u0v01⎦⎤称之为内参矩阵,矩阵
[
R
t
0
1
]
\begin{bmatrix} R& t\\ 0&1\end{bmatrix}
[R0t1]随着相机运动变化,R和旋转有关,t和平移有关,称之为外参矩阵
可这是理想情况的内外参,而真实世界总是存在许多误差
真实情况
理想的透视模型是针孔成像模型,物和像会满足相似三角形的关系。但是实际上由于相机光学系统存在加工和装配的误差,透镜就并不能满足物和像成相似三角形的关系,所以相机图像平面上实际所成的像与理想成像之间会存在畸变。畸变属于成像的几何失真,是由于焦平面上不同区域对图像的放大率不同形成的画面扭曲变形的现象,这种变形的程度从画面中心至画面边缘依次递增,主要在画面边缘反映比较明显。为了减小畸变,拍摄图片时应尽量避免用镜头焦距的最广角端或最远端拍摄。
从图像物理坐标系到像素图像坐标系的误差分析
存在,缩放,偏移,偏斜误差。
考虑这些误差后表达式变为:
把这些常数都用一个变量表示可以把内参矩阵表示为 K = [ f x s c x 0 f y c y 0 0 1 ] K = \begin{bmatrix}f_x & s & c_x \\0 & f_y & c_y \\0 & 0 & 1\end{bmatrix} K=⎣⎡fx00sfy0cxcy1⎦⎤
参数标定
内参:一般由厂商标定完成
外参:棋盘格标定法,直接线性OLT文章来源:https://www.toymoban.com/news/detail-833043.html
参考
相机模型详解_已有的相机成像模型有哪些种类-CSDN博客
计算机视觉之相机模型-CSDN博客
相机模型都没弄懂,怎么搞机器人视觉算法?_哔哩哔哩_bilibili文章来源地址https://www.toymoban.com/news/detail-833043.html
到了这里,关于相机成像模型的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!