算法：BFS宽度优先遍历

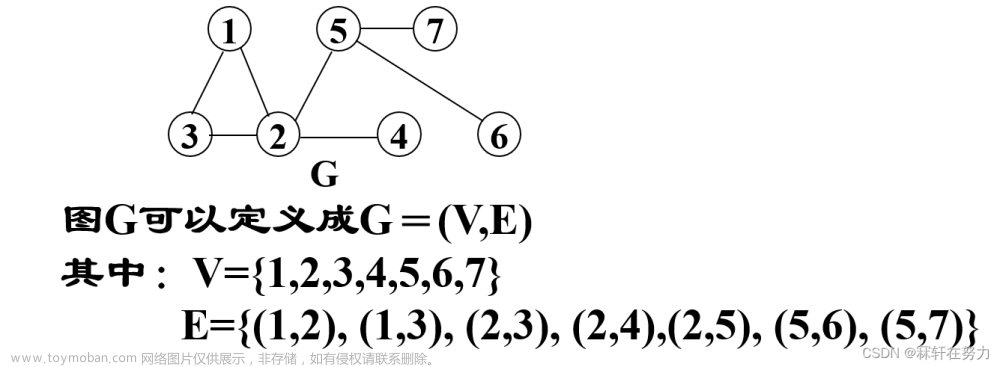
本篇总结的是BFS算法，BFS算法相比起DFS算法来说还是比较简单的

BFS与Queue相结合

N叉树的层序遍历

/*
// Definition for a Node.
class Node {
public:
    int val;
    vector<Node*> children;

    Node() {}

    Node(int _val) {
        val = _val;
    }

    Node(int _val, vector<Node*> _children) {
        val = _val;
        children = _children;
    }
};
*/

class Solution 
{
public:
    vector<vector<int>> levelOrder(Node* root) 
    {
        vector<vector<int>> ret;
        if(root == nullptr)
            return ret;
        queue<Node*> qe;
        qe.push(root);
        while(!qe.empty())
        {
            int size = qe.size();
            vector<int> tmp;
            for(int i = 0; i < size; i++)
            {
                // 取队列头节点
                Node* front = qe.front();
                qe.pop();
                // 把值入到数组中
                tmp.push_back(front->val);
                // 如果有孩子，就把孩子入到队列中
                for(int j = 0; j < (front->children).size(); j++)
                    qe.push((front->children)[j]);
            }
            ret.push_back(tmp);
        }
        return ret;
    }
};

二叉树的锯齿形层序遍历

这里提供一种双端队列的做法，也可以在合适的层数逆序

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution 
{
public:
    vector<vector<int>> zigzagLevelOrder(TreeNode* root) 
    {
        vector<vector<int>> res;
        if(root == nullptr)
            return res;
        bool status = true;
        queue<TreeNode*> qe;
        qe.push(root);
        while(!qe.empty())
        {
            int size = qe.size();
            deque<int> v;
            for(int i = 0; i < size; i++)
            {
                TreeNode* front = qe.front();
                qe.pop();
                if(status)
                    v.push_back(front->val);
                else
                    v.push_front(front->val);
                if(front->left) 
                    qe.push(front->left);
                if(front->right) 
                    qe.push(front->right);
            }
            res.push_back(vector<int>(v.begin(), v.end()));
            status = !status;
        }
        return res;
    }
};

二叉树的最大宽度

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution 
{
public:
    int widthOfBinaryTree(TreeNode* root) 
    {
        // 用数组来模拟队列，有助于最后计算，这里没用
        queue<pair<TreeNode*, unsigned int>> v;
        v.push(make_pair(root, 1));
        unsigned int lenth = 0;
        while(!v.empty())
        {
            // 计算一下这中间长度的差
            lenth = max(lenth, v.back().second - v.front().second + 1);
            int size = v.size();
            for(int i = 0; i < size; i++)
            {
                // 取头
                auto front = v.front();
                v.pop();
                // 如果有左或者有右节点，就进去
                if(front.first->left) 
                    v.push(make_pair(front.first->left, (front.second) * 2));
                if(front.first->right) 
                    v.push(make_pair(front.first->right, (front.second) * 2 + 1));
            }
        }
        return lenth;
    }
};

BFS和FLoodFill相结合

图像渲染

class Solution 
{
    int dx[4] = {1, -1, 0, 0};
    int dy[4] = {0, 0, 1, -1};
public:
    vector<vector<int>> floodFill(vector<vector<int>>& image, int sr, int sc, int color) 
    {
        int oldcolor = image[sr][sc];
        int newcolor = color;
        if(oldcolor == newcolor)
            return image;
        queue<pair<int, int>> q;
        q.push({sr, sc});
        while(!q.empty())
        {
            auto [a, b] = q.front();
            q.pop();
            image[a][b] = newcolor;
            for(int k = 0; k < 4; k++)
            {
                int x = dx[k] + a, y = dy[k] + b;
                if(x >= 0 && x < image.size() && y >=0 && y < image[0].size() && image[x][y] == oldcolor)
                    q.push({x, y});
            }
        }
        return image;
    }
};

岛屿数量

class Solution
{
    int res = 0;
    int dx[4] = { 1, -1, 0, 0 };
    int dy[4] = { 0, 0, 1, -1 };
public:
    int numIslands(vector<vector<char>>& grid)
    {
        vector<vector<bool>> check;
        check.resize(grid.size(), vector<bool>(grid[0].size(), false));
        queue<pair<int, int>> q;
        for (int i = 0; i < grid.size(); i++)
        {
            for (int j = 0; j < grid[0].size(); j++)
            {
                if (grid[i][j] == '1' && check[i][j] == false)
                {
                    check[i][j] = true;
                    q.push({ i, j });
                    while (!q.empty())
                    {
                        auto [a, b] = q.front();
                        q.pop();
                        for (int k = 0; k < 4; k++)
                        {
                            int x = dx[k] + a, y = dy[k] + b;
                            if (x >= 0 && x < grid.size() && y >= 0 && y < grid[0].size() && grid[x][y] == '1' && check[x][y] == false)
                            {
                                check[x][y] = true;
                                q.push({ x, y });
                            }
                        }
                    }
                    res++;
                }
            }
        }
        return res;
    }
};

岛屿的最大面积

class Solution 
{
public:
    int maxAreaOfIsland(vector<vector<int>>& grid) 
    {
        int res = 0, maxsize = 0, dx[4] = {1, -1, 0, 0}, dy[4] = {0, 0, 1, -1};
        vector<vector<bool>> check(grid.size(), vector<bool>(grid[0].size(), false));
        queue<pair<int, int>> q;
        for(int i = 0; i < grid.size(); i++)
        {
            for(int j = 0; j < grid[0].size(); j++)
            {
                if(check[i][j] == false && grid[i][j] == 1)
                {
                    check[i][j] = true;
                    q.push({i, j});
                    res++;
                    while(!q.empty())
                    {
                        auto [a, b] = q.front();
                        q.pop();
                        for(int k = 0; k < 4; k++)
                        {
                            int x = dx[k] + a, y = dy[k] + b;
                            if(x >= 0 && x < grid.size() && y >= 0 && y < grid[0].size() && grid[x][y] == 1 && check[x][y] == false)
                            {
                                check[x][y] = true;
                                q.push({x, y});
                                res++;
                            }
                        }
                    }
                    maxsize = max(res, maxsize);
                    res = 0;
                }
            }
        }
        return maxsize;
    }
};

BFS解决最短路问题

最小基因变化

class Solution
{
public:
	int minMutation(string startGene, string endGene, vector<string>& bank)
	{
		// 首先把符合要求的字符串丢到哈希表中
		unordered_map<string, int> hash;
		for (auto& str : bank)
			hash[str]++;
		// vis数组用来存储已经加过的状态
		unordered_map<string, int> visited;

		char arr[4] = { 'A', 'C', 'G', 'T' };
		int step = 0;
		queue<string> q;
		q.push(startGene);
		visited[startGene]++;
		while (!q.empty())
		{
			step++;
			int qsize = q.size();
			for (int k = 0; k < qsize; k++)
			{
				string front = q.front();
				q.pop();
				// 对于字符串中的每一个元素都要进行枚举
				for (int i = 0; i < front.size(); i++)
				{
					string tmp = front;
					// front中的每一个元素都要被枚举四次
					for (int j = 0; j < 4; j++)
					{
						tmp[i] = arr[j];
						// 如果front在visited中存在,说明这个元素已经被找过了
						if (visited.count(tmp) == 0)
						{
							// 如果这个元素还在bank中,那么就是有效状态,那么就可以进入队列中
							if (hash.count(tmp))
							{
								q.push(tmp);
								visited[tmp]++;
								if (tmp == endGene)
									return step;
							}
						}
					}
				}
			}
		}
		return -1;
	}
};

单词接龙

class Solution 
{
public:
    int ladderLength(string beginWord, string endWord, vector<string>& wordList) 
    {
        // 用哈希表存储符合要求的顶点和已经访问过的顶点
        unordered_map<string, int> hash;
        unordered_map<string, int> visited;
        // 把wordlist中元素存储到哈希中
        for(auto& str : wordList)
            hash[str]++;
        // 把wordlist中的元素含有的字母进行标记
        set<int> st;
        for(auto str : wordList)
        {
            for(auto e : str)
            {
                st.insert(e);
            }
        }
        int stsize = st.size();
        // 定义一些变量
        int ret = 1;
        queue<string> q;
        q.push(beginWord);
        visited[beginWord]++;
        while(!q.empty())
        {
            int qsize = q.size();
            ret++;
            for(int i = 0; i < qsize; i++)
            {
                // 进入循环中一次,就意味着走了一步
                string front = q.front();
                q.pop();
                // 单词的每一个字母都可以进行变换
                for(int j = 0; j < front.size(); j++)
                {
                    string tmp = front;
                    // 每一个字母都有26种变换方式
                    for(int k = 0; k < 26; k++)
                    {
                        // 如果这个元素在set中出现过就可以使用
                        if(st.count('a' + k))
                            tmp[j] = 'a' + k;
                        else
                            continue;
                        // 对于变换后的结果tmp,如果这个结果在list中才能继续
                        if(hash.count(tmp) && visited.count(tmp) == 0)
                        {
                            // 如果tmp没有被访问过才能继续
                            visited[tmp]++;
                            q.push(tmp);
                            if(tmp == endWord)
                                return ret;
                        }
                    }
                }
            }
        }
        return 0;
    }
};

为高尔夫比赛砍树

struct Cmp
{
	bool operator()(const pair<int, pair<int, int>>& p1, const pair<int, pair<int, int>>& p2)
	{
		return p1.first > p2.first;
	}
};

class Solution
{
	int dx[4] = { 1, -1, 0, 0 };
	int dy[4] = { 0, 0, 1, -1 };
public:
	int cutOffTree(vector<vector<int>>& forest)
	{
		int m = forest.size(), n = forest[0].size();
		// 首先要把矩阵的信息存储起来
		priority_queue<pair<int, pair<int, int>>, vector<pair<int, pair<int, int>>>, Cmp> heap;
		for (int i = 0; i < m; i++)
			for (int j = 0; j < n; j++)
				if (forest[i][j] != 1 && forest[i][j] != 0)
					heap.push(make_pair(forest[i][j], make_pair(i, j)));
		// 此时堆中就是按高度排列,并且每一个高度会对应其下标
		int step = 0;
		int x = 0, y = 0;
		while (!heap.empty())
		{
			auto top = heap.top();
			heap.pop();
			int ans = bfs(x, y, top.second.first, top.second.second, forest);
			if (ans == -1)
				return -1;
			step += ans;
			x = top.second.first;
			y = top.second.second;
		}
		return step;
	}

	// bfs函数,用来寻找从[curx, cury]到[nextx, nexty]的最短路径
	int bfs(int curx, int cury, int nextx, int nexty, vector<vector<int>>& forest)
	{
		if (curx == nextx && cury == nexty)
			return 0;
		int m = forest.size(), n = forest[0].size();
		vector<vector<bool>> visited(m, vector<bool>(n, false));
		int step = 0;
		queue<pair<int, int>> q;
		q.push({ curx, cury });
		visited[curx][cury] = true;
		while (!q.empty())
		{
			int qsize = q.size();
			step++;
			for (int i = 0; i < qsize; i++)
			{
				auto [a, b] = q.front();
				q.pop();
				for (int k = 0; k < 4; k++)
				{
					int x = a + dx[k], y = b + dy[k];
					if (x == nextx && y == nexty)
						return step;
					// 如果这个下标合法,并且没有被选过,并且不是障碍,就进队列
					if (x >= 0 && x < m && y >= 0 && y < n && visited[x][y] == false && forest[x][y] != 0)
					{
						visited[x][y] = true;
						q.push({ x, y });
					}
				}
			}
		}
		return -1;
	}
};

拓扑排序

课程表

class Solution 
{
public:
    bool canFinish(int numCourses, vector<vector<int>>& prerequisites) 
    {
        // 1. 建图
        // 一个用来存储图的边信息,一个用来存储图的入度信息
        unordered_map<int, vector<int>> graph;
        vector<int> in(numCourses);

        // 2. 把图的信息存储到图中
        for(auto& e : prerequisites)
        {
            int pre = e[1], next = e[0];
            graph[pre].push_back(next);
            in[next]++;
        }

        // 3. 多源bfs遍历
        queue<int> q;
        for(int e = 0; e < numCourses; e++)
            if(in[e] == 0)
                q.push(e);
        while(!q.empty())
        {
            int front = q.front();
            q.pop();
            for(auto e : graph[front])
            {
                in[e]--;
                if(in[e] == 0)
                    q.push(e);
            }
        }

        // 4. 判断有没有环
        for(auto e : in)
            if(e)
                return false;
        return true;
    }
};

课程表II

class Solution 
{
public:
    vector<int> findOrder(int numCourses, vector<vector<int>>& prerequisites) 
    {
        vector<int> res;

        // 1. 建表
        unordered_map<int, vector<int>> graph;
        vector<int> in(numCourses);

        // 2. 把信息入表
        for(auto e : prerequisites)
        {
            int prev = e[1], next = e[0];
            graph[prev].push_back(next);
            in[next]++;
        }

        // 3. 多源bfs
        queue<int> q;
        // 把入度为0的点入到队列中
        for(int i = 0; i < numCourses; i++)
            if(in[i] == 0)
                q.push(i);
        while(!q.empty())
        {
            int front = q.front();
            q.pop();
            res.push_back(front);
            for(auto& e : graph[front])
            {
                in[e]--;
                if(in[e] == 0)
                {
                    q.push(e);
                }
            }
        }

        // 4. 判环
        for(int i = 0; i < numCourses; i++)
            if(in[i])
                return {};
        return res;
    }
};

火星词典

文章来源地址https://www.toymoban.com/news/detail-834483.html

class Solution 
{
    // 1. 建图
    unordered_map<char, unordered_set<char>> edge;
    unordered_map<char, int> in;
    bool check;
public:
    string alienOrder(vector<string>& words) 
    {
        for(auto& str : words)
            for(auto& ch : str)
                in[ch] = 0;

        string res;
        // 2. 存储信息
        int n = words.size();
        for(int i = 0; i < n; i++)
            for(int j = i + 1; j < n; j++)
                add(words[i], words[j]);
        if(check)
            return "";
        
        // 3. 拓扑排序
        queue<char> q;
        for(auto& [a, b] : in)
            if(b == 0)
                q.push(a);

        while(!q.empty())
        {
            char front = q.front();
            q.pop();
            res += front;
            for(auto& ch : edge[front])
            {
                in[ch]--;
                if(in[ch] == 0)
                    q.push(ch);
            }
        }

        // 4. 检查
        for(auto& [a, b] : in)
            if(b)
                return "";
        return res;
    }

    void add(string& s1, string& s2)
    {
        int n = min(s1.size(), s2.size());
        
        int i = 0;
        for(; i < n; i++)
        {
            if(s1[i] != s2[i])
            {
                char a = s1[i], b = s2[i];
                if(edge.count(a) == 0 || edge[a].count(b) == 0)
                {
                    edge[a].insert(b);
                    in[b]++;  
                }
                break;
            }
        }

        if(i == s2.size() && i < s1.size())
            check = true;
    }
};

到了这里，关于算法：BFS宽度优先遍历的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！