目录
前言
课题背景和意义
实现技术思路
一、 算法理论基础
1.1 卷积神经网络
1.3 EM算法
二、实验及结果分析
2.1 数据处理
2.2 模型训练
3.2 结果分析
最后
前言
📅大四是整个大学期间最忙碌的时光,一边要忙着备考或实习为毕业后面临的就业升学做准备,一边要为毕业设计耗费大量精力。近几年各个学校要求的毕设项目越来越难,有不少课题是研究生级别难度的,对本科同学来说是充满挑战。为帮助大家顺利通过和节省时间与精力投入到更重要的就业和考试中去,学长分享优质的选题经验和毕设项目与技术思路。
🚀对毕设有任何疑问都可以问学长哦!
选题指导:
最新最全计算机专业毕设选题精选推荐汇总
大家好,这里是海浪学长毕设专题,本次分享的课题是
🎯基于机器学习的票据表格分割识别系统
课题背景和意义
在许多业务场景中,如财务会计、发票管理和报销流程等,准确地分割和识别票据表格中的信息是必要的任务。它能够为各种业务场景提供科学工具和决策支持,提高票据处理的效率和准确性,推动自动化文档识别和数据智能化的发展与应用。
实现技术思路
一、 算法理论基础
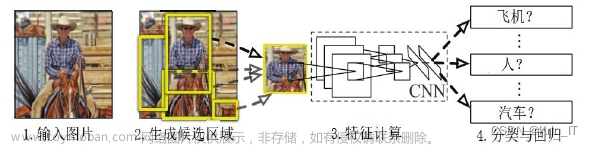
1.1 卷积神经网络
深度学习指从有限样例中,通过算法总结出一般规律, 并可以应用到新的未知数据上,可供学习的数据越多,其效果越好。从根源来讲, 深度学习是机器学习的一个分支。卷积核的数量和卷积层的数量都对卷积神经网络的性能和拟合能力产生影响。适当增加卷积核的数量和卷积层的数量可以提高网络的表达能力和学习能力,但过多的卷积核和层数可能导致噪声和冗余。因此,在设计和改进神经网络模型时,需要在广度和深度方面进行权衡和调整,以达到更好的性能和鲁棒性。

卷积核的数量决定了网络能够提取多少种特征图。较多的卷积核可以捕捉更多的图像特征,每个卷积核对应一种特征。适当增加卷积核的数量可以提高网络的表达能力。然而,当卷积核的数量过多时,可能会引入噪声或冗余信息,影响网络的性能。卷积层的数量决定了网络的深度,即网络的层数。较深的网络可以通过堆叠多层特征提取器来丰富网络的表达能力。低层卷积层主要提取局部细节特征,高层卷积层则能够提取更抽象的全局特征。增加网络的深度可以提高网络的非线性表示能力,提高对复杂模式的学习能力。

1.3 EM算法
EM算法(Expectation-Maximization Algorithm)是一种迭代算法,用于估计含有潜在变量的概率模型的参数。给定观测数据Y,其概率分布为P(Y|θ),其中θ是需要估计的模型参数。EM算法的目标是通过极大化不完全数据Y关于参数θ的对数似然函数的下界来逼近极大化完全数据对数似然函数的最大似然估计。
具体步骤如下:
- 初始化模型参数θ的初值。
- E步(Expectation Step):计算完全数据的期望对数似然函数的期望,即计算潜在变量的条件概率分布。
- M步(Maximization Step):针对给定的潜在变量的条件概率分布,最大化完全数据的对数似然函数关于参数θ的期望。
- 重复执行E步和M步,直到收敛,得到模型的最大似然估计或近似最大似然估计。

相关代码示例:
# 初始化模型参数
initialize_parameters()
# 迭代过程
while not converged:
# E步(Expectation Step)
expectation()
# M步(Maximization Step)
maximization()
# 判断是否收敛
if is_converged():
converged = True
# 输出最终的参数估计值
output_parameters()EM算法的核心思想是通过迭代求解下界来逼近极大化完全数据对数似然函数的最大似然估计。由于EM算法涉及到对不完全数据的期望和对完全数据的最大化,它可以克服含有潜在变量的概率模型参数估计中的困难。

EM算法是一种用于含有潜在变量的概率模型参数估计的迭代算法,通过迭代求解下界来逼近极大化完全数据对数似然函数的最大似然估计。它能够解决模型含有潜在变量时无法直接使用传统估计方法的问题,并在多峰数据建模中具有一定的应用价值。然而,EM算法只能保证局部最优解,对于全局最优解没有保证。

相关代码示例:
for iteration in range(max_iterations):
# E步(Expectation Step)
compute_lower_bound()
# M步(Maximization Step)
maximize_lower_bound()二、实验及结果分析
2.1 数据处理
收集大量的票据图像数据,包括各种类型的票据,例如发票、收据、订单等。可以通过网络爬虫、合作伙伴提供的数据或者自行采集等方式获取。确保数据集的多样性,涵盖不同票据样式、字体、背景和布局等方面的变化。这样能够帮助系统更好地适应各种实际场景。根据需要,进行数据标注,包括整体图像的标注和表格区域的标注。表格区域的标注可以使用矩形框或多边形来表示。

在数据预处理阶段,要对图像进行清洗、调整大小、灰度化和增强等处理,以提高图像质量和可分辨性。这样的数据准备工作为后续的表格检测、文本识别和模型训练提供了高质量、多样性的数据基础。
相关代码示例:
image = cv2.imread('invoice.jpg')
# 图像清洗
# 可根据需要进行噪声去除、平滑处理等操作
# 图像调整大小
resized_image = cv2.resize(image, (800, 600)) # 调整为800x600的大小
# 灰度化
gray_image = cv2.cvtColor(resized_image, cv2.COLOR_BGR2GRAY)
# 图像增强
enhanced_image = cv2.equalizeHist(gray_image) # 直方图均衡化
# 显示原始图像和预处理后的图像
cv2.imshow('Original Image', image)
cv2.imshow('Preprocessed Image', enhanced_image)
cv2.waitKey(0)
cv2.destroyAllWindows()2.2 模型训练
通过实验和算法的组合,包括标准化处理、JDM网络和CPD算法,可以在合成表格数据集上实现高准确率和召回率的交叉点检测,并且能够实现高精度的表格分割。

相关代码示例:
# 导入所需的库和模块
import numpy as np
import cv2
# 导入JDM网络和CPD算法的相关模块(需自行实现或使用现有的实现)
# 定义函数进行标准化处理
def standardize(image):
# 实现图像的标准化处理
# ...
# 定义函数进行表格交叉点检测
def detect_cross_points(image):
# 使用JDM网络实现表格交叉点检测
# ...
# 定义函数进行表格分割
def segment_tables(image):
# 使用CPD算法实现表格分割
# ...
# 读取图像
image = cv2.imread('table_image.jpg')
# 图像预处理
image = standardize(image)
# 进行表格交叉点检测
cross_points = detect_cross_points(image)
# 进行表格分割
table_regions = segment_tables(image)
# 显示交叉点和分割结果
# ...在进行点集匹配之前,首先对两个点集进行标准化处理。经过实验测试发现,经过标准化处理后的点集在面对旋转和点缺失等问题时能够获得更好的匹配效果。本次实验中采用了JDM网络提取交叉点时具有较高召回率和准确率的特点,以及CPD算法在处理点缺失和点冗余时表现良好。在测试集中,交叉点的匹配正确率达到了100%,即所有票据中的点都能够找到与之对应的模板中的点。

测试集上,如果严格采用四个顶点表示单元格,则表格分割准确率为97.4%。如果认为对角线上的两个点也能表示单元格,则表格分割准确率可达到98.6%。第一列是增值税发票的分割结果,第二列是购车发票的分割结果,第三列是税收完税证明的分割结果。使用四个顶点分割出的单元格标出了两条对角线,而使用两个点分割出的单元格只标出了一条对角线,对于未分割出的单元格则没有标示。

最后
我是海浪学长,创作不易,欢迎点赞、关注、收藏。文章来源:https://www.toymoban.com/news/detail-834508.html
毕设帮助,疑难解答,欢迎打扰!文章来源地址https://www.toymoban.com/news/detail-834508.html
到了这里,关于毕业设计选题:基于机器学习的票据表格分割识别系统 人工智能 YOLO 计算机视觉的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!