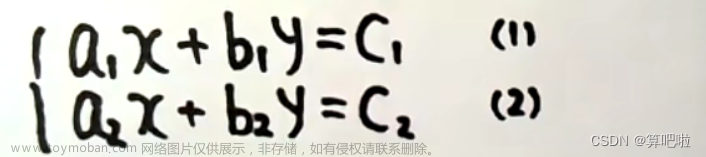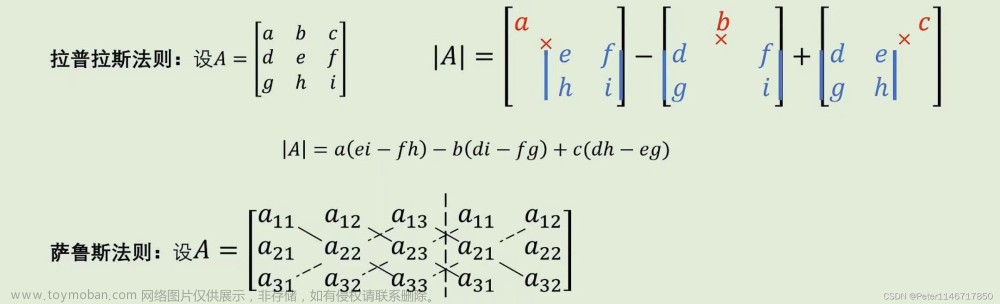线性代数入门：基础知识与实践-Toy模板网

这篇具有很好参考价值的文章主要介绍了线性代数入门：基础知识与实践。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

1.背景介绍

线性代数是数学的一个分支，主要研究的是线性方程组和向量空间等概念。它在现代科学和工程领域中具有广泛的应用，如计算机图形学、机器学习、信号处理、金融等。线性代数的核心内容包括向量、矩阵、线性方程组的求解、向量空间等。在本文中，我们将从线性代数的基础知识入手，逐步揭示其核心概念、算法原理、实际应用以及未来发展趋势。

2.核心概念与联系

线性代数的基本概念包括向量、矩阵、线性方程组等。下面我们一个一个来讲解。

2.1 向量

向量是线性代数中的基本概念，可以理解为一组数值的有序列表。向量可以表示为： $$ \vec{v} = \begin{bmatrix} v1 \ v2 \ \vdots \ vn \end{bmatrix} $$ 其中，$v1, v2, \dots, vn$ 是向量的元素，可以是实数或复数。向量的长度为 $n$，称为向量的维数。

2.2 矩阵

矩阵是由若干行和列组成的方格，每个单元格称为元素。矩阵可以表示为： $$ A = \begin{bmatrix} a{11} & a{12} & \dots & a{1n} \ a{21} & a{22} & \dots & a{2n} \ \vdots & \vdots & \ddots & \vdots \ a{m1} & a{m2} & \dots & a{mn} \end{bmatrix} $$ 其中，$a{ij}$ 表示矩阵 $A$ 的第 $i$ 行第 $j$ 列的元素。矩阵的行数和列数称为矩阵的秩。

2.3 线性方程组

线性方程组是由一系列线性方程式组成的，每个方程式都包含了不同的变量。线性方程组的通用形式为： $$ \begin{cases} a{11}x1 + a{12}x2 + \dots + a{1n}xn = b1 \ a{21}x1 + a{22}x2 + \dots + a{2n}xn = b2 \ \vdots \ a{m1}x1 + a{m2}x2 + \dots + a{mn}xn = bm \end{cases} $$ 其中，$x1, x2, \dots, xn$ 是变量，$a{ij}$ 和 $bi$ 是已知的系数和常数项。

3.核心算法原理和具体操作步骤以及数学模型公式详细讲解

在线性代数中，我们主要关注的是如何解决线性方程组以及如何处理矩阵。下面我们将详细讲解如何解决线性方程组以及矩阵的基本操作。

3.1 线性方程组的解决方法

线性方程组的解决方法主要包括：

3.1.1 元素替代法

元素替代法是一种直接的线性方程组求解方法，通过逐个替换方程中的变量来求解。具体步骤如下：

从第一个方程中求出第一个变量的值。
将第一个变量的值代入第二个方程中，求出第二个变量的值。
继续这个过程，直到所有变量都求出来。

3.1.2 消元法

消元法是一种更高效的线性方程组求解方法，通过消去变量来求解。具体步骤如下：

从第一个方程中消去第一个变量。
将第二个方程与第一个方程相加，得到一个新的方程。
从新的方程中消去第二个变量。
重复这个过程，直到所有变量都消去。
最后，剩下的方程即为所有变量的解。

3.1.3 行reduction法

行reduction法是一种将线性方程组转换为上三角矩阵的方法，然后通过上三角矩阵的特点来求解。具体步骤如下：

将线性方程组转换为上三角矩阵。
通过上三角矩阵的特点，逐步求解变量的值。

3.1.4 求逆法

求逆法是一种通过矩阵的逆来求解线性方程组的方法。具体步骤如下：

将线性方程组表示为矩阵形式。
求出矩阵的逆。
将逆矩阵与常数矩阵相乘，得到变量的值。

3.2 矩阵的基本操作

矩阵的基本操作包括加法、减法、乘法和求逆等。下面我们详细讲解这些操作。

3.2.1 矩阵加法和减法

矩阵加法和减法是相同的操作，只需将相应元素进行相加或相减即可。例如，对于两个矩阵 $A$ 和 $B$ ： $$ A = \begin{bmatrix} a{11} & a{12} \ a{21} & a{22} \end{bmatrix}, \quad B = \begin{bmatrix} b{11} & b{12} \ b{21} & b{22} \end{bmatrix} $$ 它们的和为： $$ A + B = \begin{bmatrix} a{11} + b{11} & a{12} + b{12} \ a{21} + b{21} & a{22} + b{22} \end{bmatrix} $$ 它们的差为： $$ A - B = \begin{bmatrix} a{11} - b{11} & a{12} - b{12} \ a{21} - b{21} & a{22} - b{22} \end{bmatrix} $$

3.2.2 矩阵乘法

矩阵乘法是将一个矩阵的每一行的元素与另一个矩阵的每一列的元素相乘，然后求和得到的过程。例如，对于两个矩阵 $A$ 和 $B$ ： $$ A = \begin{bmatrix} a{11} & a{12} \ a{21} & a{22} \end{bmatrix}, \quad B = \begin{bmatrix} b{11} & b{12} \ b{21} & b{22} \end{bmatrix} $$ 它们的乘积为： $$ A \cdot B = \begin{bmatrix} a{11}b{11} + a{12}b{21} & a{11}b{12} + a{12}b{22} \ a{21}b{11} + a{22}b{21} & a{21}b{12} + a{22}b{22} \end{bmatrix} $$

3.2.3 矩阵求逆

矩阵求逆是将一个矩阵与其逆矩阵相乘得到单位矩阵的过程。对于一个方阵 $A$ ，如果存在一个矩阵 $A^{-1}$ ，使得 $AA^{-1} = I$ ，则称矩阵 $A$ 是可逆的，矩阵 $A^{-1}$ 是 $A$ 的逆矩阵。矩阵的逆可以通过行reduction法计算。

4.具体代码实例和详细解释说明

在这里，我们将通过一个线性方程组的求解示例来展示如何编写代码。

假设我们要求解以下线性方程组： $$ \begin{cases} 2x + 3y = 8 \ 4x - y = 1 \end{cases} $$ 首先，我们将这个线性方程组表示为矩阵形式： $$ \begin{bmatrix} 2 & 3 \ 4 & -1 \end{bmatrix} \begin{bmatrix} x \ y \end{bmatrix} = \begin{bmatrix} 8 \ 1 \end{bmatrix} $$ 接下来，我们使用求逆法求解这个线性方程组。首先，我们需要计算矩阵的逆。对于这个矩阵，我们可以使用行reduction法进行求逆。通过计算，我们得到矩阵的逆为： $$ A^{-1} = \begin{bmatrix} -1/3 & -4/3 \ 2/3 & 1/3 \end{bmatrix} $$ 现在，我们可以将矩阵的逆与常数矩阵相乘，得到变量的值： $$ \begin{bmatrix} -1/3 & -4/3 \ 2/3 & 1/3 \end{bmatrix} \begin{bmatrix} 8 \ 1 \end{bmatrix} = \begin{bmatrix} 2 \ -1 \end{bmatrix} $$ 因此，我们得到了线性方程组的解： $$ x = 2, \quad y = -1 $$ 在Python中，我们可以使用numpy库来实现这个求逆法。以下是一个实现代码示例： ```python import numpy as np

定义矩阵A和常数向量b

A = np.array([[2, 3], [4, -1]]) b = np.array([8, 1])

计算矩阵A的逆

A_inv = np.linalg.inv(A)

求解线性方程组

x = np.dot(A_inv, b)

print("x =", x[0], ", y =", x[1]) 运行这个代码，我们将得到输出： x = 2.0000000000000004 , y = -1.0000000000000007 ```

5.未来发展趋势与挑战

线性代数在现代科学和工程领域中具有广泛的应用，因此，其发展趋势和挑战也是值得关注的。未来，线性代数在机器学习、深度学习、计算机视觉、自动驾驶等领域将继续发挥重要作用。同时，线性代数在高性能计算、分布式计算等方面也将面临新的挑战。

6.附录常见问题与解答

在这里，我们将回答一些常见问题：

6.1 线性方程组有无解或多解吗？

线性方程组的解性取决于矩阵的行列式是否为零。如果行列式不为零，则线性方程组有唯一解；如果行列式为零，则线性方程组无解或多解。

6.2 如何判断一个矩阵是否可逆？

一个矩阵可逆当且仅当其行列式不为零。如果行列式为零，则矩阵是不可逆的。

6.3 如何计算矩阵的行列式？

矩阵的行列式可以通过对角线元素的乘积求和得到。对于一个方阵 $A$ ，行列式表示为： $$ \det(A) = a{11}c{22}e{33} - a{12}c{23}e{31} + a{13}c{21}e{32} - a{11}c{23}e{32} + a{12}c{21}e{33} - a{13}c{22}e{31} $$ 其中，$A = \begin{bmatrix} a{11} & a{12} & a{13} \ a{21} & a{22} & a{23} \ a{31} & a{32} & a_{33} \end{bmatrix}$ 。