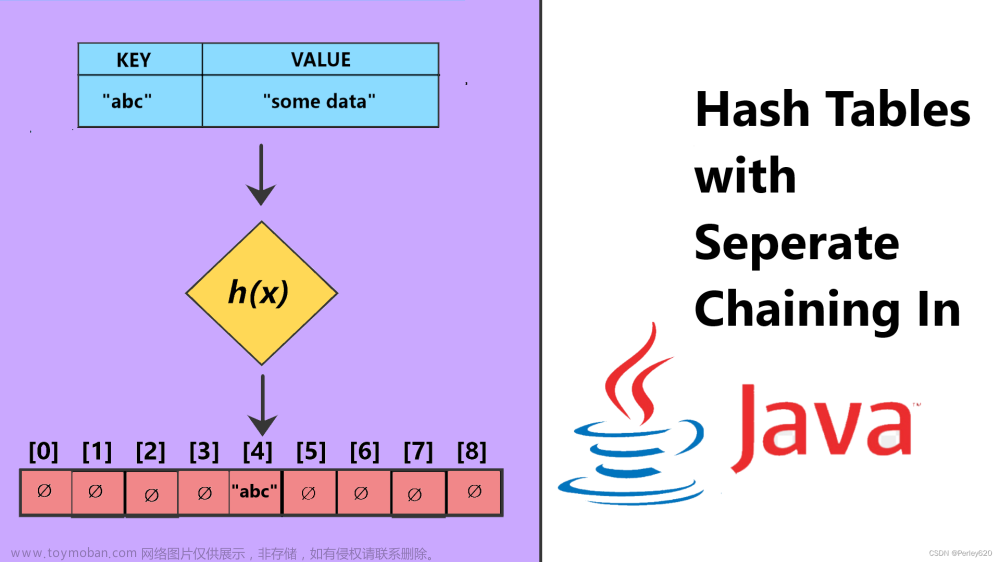
哈希思想
在顺序和树状结构中,元素的存储与其存储位置之间是没有对应关系,因此在查找一个元素时,必须要经过多次的比较。
顺序查找的时间复杂度为0(N),树的查找时间复杂度为log(N)。
我们最希望的搜索方式:通过元素的特性,不需要对比查找,而是直接找到某个元素。
这一个通过key与存储位置建立一一的思想就是hash思想。
哈希表就是基于哈希思想的一种具体实现。哈希表也叫散列表,是一种数据结构。无论有多少条数据,插入和查找的时间复杂度都是O(1),因此由于其极高的效率,被广泛使用。
建立映射关系:
例如集合{8,5,6,3,7,2,1,0}key为每个元素的值,capaticy为哈希表元素的容量。
映射过程:
元素8 key=8 8%10=8 映射在数组下标为第8的位置上元素7 映射在下标为7的位置上
- 直接定值法:(关键数范围集中,量不大的时候)关键字和存储位置是一一对应,不存在哈希冲突
- 除留余数法:(关键字很分散,量很大)关键字和存储位置是一对多的关系,存在哈希冲突
哈希冲突
对于两个数据元素的关键字 和 (i != j),有 != ,但有:Hash() == Hash(),即:不同关键字通过相同哈希函数计算出相同的哈希地址,该种现象称为哈希冲突或哈希碰撞
例如上述的举例:
key的值为 18 15的时候
hashi计算的方法得出 需要映射到8 和5的位置上,但是8 和5的位置已经存在其它值。这就产生了冲突
哈希冲突的解决
1.开放定址法(闭散列)
a:线性探测
如果发生冲突,就往后一次一步寻找为空的位置。
b:二次探测
发生冲突,每次往后走俩步,寻找没有冲突的位置。
线性探测的缺点:容易产生成片的冲突
二次探测的缺点:虽然解决了容易产生成片冲突,但是空间利用率也不高
2.开散列
又称开链法、哈希桶,计算如果产生了哈希冲突,就以链表的形式将冲突的值链接起来。

哈希表的闭散列实现
闭散列哈希中的,每个位置不仅需要存储数据,还需要标注状态,方便查找删除。
enum State { EMPTY, EXIST, DELETE };
标记状态的意义?
在一个哈希表中,如果需要存放,我们会计算出key映射位置。如果key映射位置被占走,会往后继续寻找到删除/空的位置放置。
在查找时,在映射位置找不到时,需要往后寻找,我们不可能一直往后寻找O(N).,那就失去哈希表的价值,当我们遇到存在/删除位置时继续往后寻找,直到找到空位置,说明没有该元素。
因此在存储时,每个位置都必须有状态和数据
struct Elem
{
pair<K, V> _val;
State _state;
};框架
希表还需要维持容量的问题。因此需要_size表示实际存放,来维持负载因子
template<class K,class V> //k—v结构
class HashTable
{
public:
//...
private:
vector<Elem> _ht;
size_t _size; //实际存储
size_t _totalSize; // 哈希表中的所有元素:有效和已删除, 扩容时候要用到
};哈希表的插入
- 根据K查找是为空,是则返回false
- 计算负载因子,是否需要扩容
- 插入新元素
- 更新位置状态,有效数目增加
扩容的方法
- 开新的哈希表(默认空间为原来的2倍)
- 遍历旧表,调用哈希表的插入。
- 交换俩个表。

// 插入
bool Insert(const pair<K, V>& val)
{
if (Find(val.first) != -1)
return false;
//负载因子为7时,扩容
if ((_size * 10) / _ht.size() == 7)
{
size_t newsize = _ht.size() * 2;
HashTable<K, V>newht;
newht._ht.resize(newsize);
//遍历旧表
for (size_t i = 0; i < _ht.size(); i++)
{
if (_ht[i]._state == EXIST)
newht.Insert(_ht[i]._val);
}
_ht.swap(newht._ht);
}
//出入新元素
size_t hashi = HashFunc(val.first);
while (_ht[hashi]._state == EXIST)
{
++hashi;
hashi %= _ht.size();
}
_ht[hashi]._val = val;
_ht[hashi]._state = EXIST;
++_size;
++_totalSize;
return true;
}哈希表的查找
通过hash函数映射到hashi,往后一直比对,遇到存在比对,不是要找的val就往后需要,遇到删除也往后对比。直到遇到空返回。
// 查找
size_t Find(const K& key)
{
size_t hashi = HashFunc(key);
while (_ht[hashi]._state != EMPTY)
{
if (_ht[hashi]._state == EXIST
&& _ht[hashi]._val.first == key)
{
return hashi;
}
++hashi;
hashi %= _ht.size();
}
return -1;
}哈希表的删除
删除是比较简单,是一种伪删除,不需要对数据清楚,只需要修改状态为删除,减少有效个数
- 调用find,没有则返回flase
- 修改为状态
- 减少个数
bool Erase(const K& key)
{
int hashi = Find(key);
if (hashi == -1) return false;
_ht[hashi]._state = DELETE;
--_size;
return true;
}这三部分就是闭散列的主体结构。需要维持负载因子和状态。
Gitee: 闭散列哈希代码
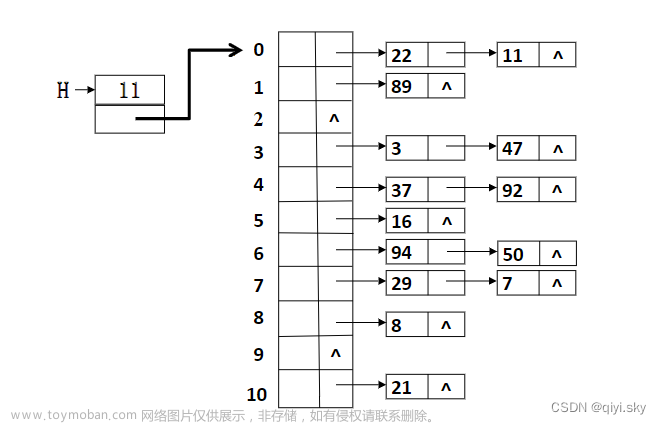
哈希桶
开散列哈希表就不要需要状态的使用,是由一个链表的数组构成。
就是一排一排的桶。想要查找数据,只需要映射位置,在桶中寻找,是O(1)的放法.
特别极端情况下可能达到O(N)。
框架
底层可以依赖单链表,只需要简单的头插即可。
链表的结点:需要包含下一个位置的指针,需要包含pair键值对
template<class K, class V>
struct HashNode
{
pair<K, V>_kv;
HashNode<K, V>* _next;
//构造
HashNode(const pair<K, V>& kv)
:_kv(kv)
, _next(nullptr)
{}
};同样需要记录表中有效元素的个数,但是一般情况下,负载因子在80%-90%效率最大
我们为了简单实现,在100%时才扩容。
template<class K, class V>
class HashTable
{
public:
//...
private:
vector<Node*> _table; //哈希表
size_t _n = 0; //哈希表中的有效元素个数
};哈希桶的插入
- 检查是否为已经存在的Key
- 检查负载因子,为1就扩容
- 往hashi位置头插插入
- 修改个数
扩容的方法
- rasize一个二倍数量的原表
- 遍历旧表,将一个元素从链表的头取下,插入到新表中的hashi位置上。注意保存下一个位置!
- 交换俩张表

bool Inset(const pair<K, V>& kv)
{
if (Find(kv.first))
{
return false;
}
hash hf;
//扩容
if (_tables.size() == _n)
{
size_t newsize = _tables.size() * 2;
vector<Node*> newtable;
newtable.resize(newsize, nullptr);
for (size_t i = 0; i < (_tables.size()); i++)
{
Node* cur = _tables[i];
while (cur)
{
Node* next = cur->_next;
size_t hashi = hf(cur->_kv.first % newtable.size());
//头插
cur->_next = newtable[hashi];
newtable[hashi] = cur;
cur = next;
}
_tables[i] = nullptr;
}
_tables.swap(newtable);
}
size_t hashi = hf(kv.first) % _tables.size();
Node* newnode = new Node(kv);
newnode->_next = _tables[hashi];
_tables[hashi] = newnode;
_n++;
return true;
}哈希桶的查找
- 计算hashi
- 遍历单链表
- 为空则返回flase
Node* Find(const K& key)
{
hash fc;
size_t hashi = fc(key) % _tables.size();
Node* cur = _tables[hashi];
while (cur)
{
if (cur->_kv.first == key)
return cur;
cur=cur->_next;
}
return nullptr;
}哈希桶的删除
删除需要主要是删除的中间结点还是首结点
需要保存父亲结点
和单链表的删除基本一致
bool Erase(const K& key)
{
hash fc;
size_t hashi = fc(key) % _tables.size();
Node* cur = _tables[hashi];
Node* prev = nullptr;
while (cur)
{
//找到了
if (cur->_kv.first == key)
{
//头删
if (prev == nullptr)
{
_tables[hashi] = cur->_next;
}
else
{
prev->_next = cur->_next;
}
delete cur;
return true;
}
}
return false;
}Gitee: 开散列哈希桶代码
关于仿函数HashFunc
仿函数是一种回调,可以定义出函数对象。
是对不同类型转化为key,之前在位图就已经介绍,本文用的是BDK算法
对于string字符串类型会有存在冲突,但是可以通过不同的算法映射到不到的位置上,通过几个值的比对能减少失误的概率。
template<class K>
struct DefaultHash
{
size_t operator()(const K& key)
{
return (size_t)key;
}
};
//特化 针对字符串
template<>
struct DefaultHash<string>
{
size_t operator()(const string& key)
{
//BKDR
size_t hash = 0;
for (auto ch : key)
{
hash = hash * 131 + ch;
}
return hash;
}
};文章来源地址https://www.toymoban.com/news/detail-834565.html文章来源:https://www.toymoban.com/news/detail-834565.html
到了这里,关于【数据结构】哈希表的开散列和闭散列模拟的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!