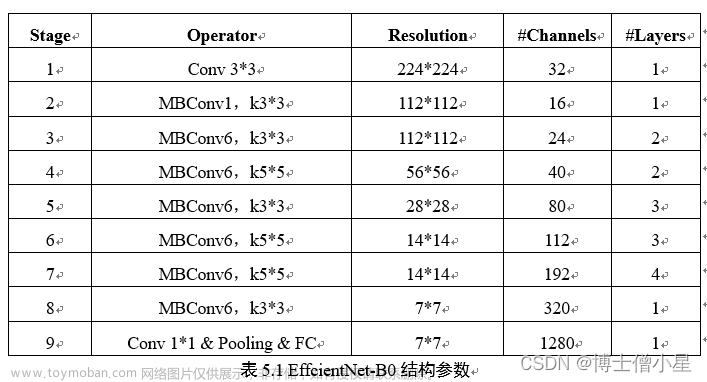
1.基本概念
（1）定义：决策树:基于树结构进行决策的处理机制，不断根据某属性进行划分的过程，通常会进行一系列的判断或是“子决策”。
（2）策略：“分而治之”，递归进行。
（3）解释：如下图，当我们需要判断一个西瓜是否为好瓜，我们先判断色泽是否为青绿，如果为正，我们继续进行下一个判断。
显然，我们能够明白每一个决策都是建立在之前决策的基础之上的，决策树的最终目的是将样本越分越”纯“。
-
从逻辑角度，是if-else语句的组合
-
从几何角度，是根据某种准则划分特征空间
（4）递归停止条件：
-
对于一个节点，全是同类样本，那不用执行下一步细分判断
-
对于一个节点，仍然有异类样本，但是没有下一个属性去判断了，也要终止
-
对于一个属性的其中一个分类，若数据集中的数据完全没有对应分类中的数据，即空集，那也要终止。
信息论知识 补充：
自信息：
,本质上就是一个单位，当b=2时单位为bit,当b=e时单位为nat
随机变量X的每个取值x都对应一个p(x)
信息熵（自信息的期望）：度量随机变量X的不确定性，信息熵越大越不确定。公式如下：
对信息熵的理解：其实我们看随机变量X，注意它是一个变量，它是不确定的，当我们某个取值最大时，比如等于p（x=a）=1,那么变量就变成了常量，那其他x取值的概率都等于0，此时信息熵是最小的。当所有可能取值的概率都相等时，信息熵最大，不确定性最大。
熵的增益：上一层的熵-当前一层熵的总和
-
数学意义：熵的变化量
-
决策树：根节点的熵-当前子节点的熵的和
众所周知，一个数据集/事物涵盖了许多属性，如何确定划分属性？
比如，一个西瓜的属性有根蒂，敲声，纹理，颜色，触感等等
总体思路：计算每个属性的信息增益，比较其大小，大者则被选为划分属性
如何计算：
我们看如下例子：
分析数据集，有17个训练样例|y|=2，正例8个，占8/17，反例9个，占9/17
对于根节点，其信息熵为：
以属性“色泽”为例，
由上例，可以计算出每一个属性的信息增益，然后比较其大小，大的就被作为“划分属性”
实际上，信息增益追求的就是每次能尽可能的将划分结果分的干净一点。
但是，我们进一步想，这样做会不会使得其划分属性会尽可能多呢？，因为属性越多越精细自然分到每个属性的数据量越少，也就越干净。
比如说，我们拿到了人这个数据集，那如果根据【电话号码】这个属性进行划分，可想而知，每个电话号码下对应一个人，是足够干净的，但是我们并不想这样做，别忘了机器学习的目的是根据已有样本对未知数据进行预测，如果此时再来一个人的数据，我们无法对他进行分类，那这个模型的构建显然是泛化能力极低的。
所以我们提出对ID3算法的进一步改进，即增益率\
其中IV（a）指的是分支率，Gain指的是增益大小，我们希望的是，分支尽可能少而且增益尽可能大
对于C4.5算法中，我们采用启发式的办法：先从候选划分属性中找出信息增益水平高于平均水平的，在从中选取增益率最高的。
技巧：其实，上述行为体现的是一种规范化的思想，本来对于不同属性，其分支不同，是不能直接比较的，但是我们将其规范化，就变得可比较了
特殊形式：归一化:将数值规范到【0,1】之间
其他划分标准：基尼指数：从一个袋子里随便抓两个球，若为同类则表示纯度为1，用1-纯度，则表示其不纯度，我们将其最小化，则Gini越小，数据集的纯度越高。
决策树剪枝（pruning）
-
目的：防止决策树过拟合的最根本方法
-
做法：因为可能会导致分支过多，所以主动去掉一些分支
通常，使用单只决策树的时候是需要进行剪枝操作的
-
基本策略：
-
预剪枝（pre-pruning）:提前终止某些分支的生长
-
后剪枝（post-pruning）:生成一棵完全树，再“回头”剪枝
-
当处理多维数据时，我们经常会遇到样本属性值缺失的问题，如果直接扔掉，会造成对数据的极大浪费
如何解决？涉及到以下两个问题：
Q1：如何进行划分属性选择？
Q2:定划分属性，若样本在该属性上的值缺失，如何进行划分？
基本思路：样本赋权，权重划分
文章来源：https://www.toymoban.com/news/detail-834768.html
文章来源地址https://www.toymoban.com/news/detail-834768.html
到了这里，关于机器学习实录——决策树的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！
