【模板】负环问题题解（spfa和bellman解决）-Toy模板网

这篇具有很好参考价值的文章主要介绍了【模板】负环问题题解（spfa和bellman解决）。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

P3385 【模板】负环

题目描述

给定一个 n 个点的有向图，请求出图中是否存在从顶点 11 出发能到达的负环。

负环的定义是：一条边权之和为负数的回路。

输入格式

本题单测试点有多组测试数据。

输入的第一行是一个整数 T，表示测试数据的组数。对于每组数据的格式如下：

第一行有两个整数，分别表示图的点数 n 和接下来给出边信息的条数 m。

接下来 m 行，每行三个整数 u,v,w。

若 w≥0，则表示存在一条从 u 至 v 边权为 w 的边，还存在一条从 v 至 u 边权为 w 的边。
若 w<0，则只表示存在一条从 u 至 v 边权为 w 的边。

输出格式

对于每组数据，输出一行一个字符串，若所求负环存在，则输出 YES，否则输出 NO。

输入输出样例

输入 #1复制

输出 #1复制

NO
YES

说明/提示

数据规模与约定

对于全部的测试点，保证：

1≤n≤2×103，1≤m≤3×103。
1≤u,v≤n，−−104≤w≤104。
1≤T≤10。

提示

请注意，m 不是图的边数。

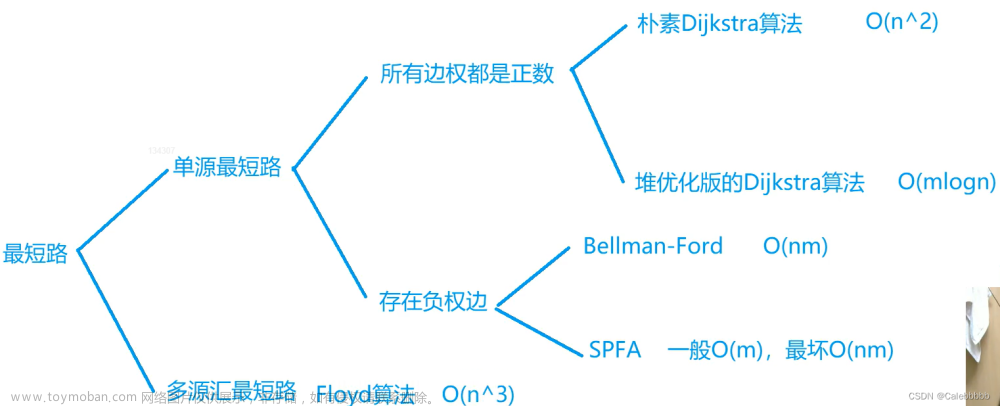
对于存在负环的问题，我们通常使用bellman或者spfa算法（bellman的队列优化）判断有无负环

bellman解决思路：

Bellman-Ford 算法通过不断迭代计算最短路，每轮迭代至少有一个结点得到了最短路。所以，若图中没有负环，则最多经过 n−1 轮迭代后算法结束。若第 n 轮迭代仍有结点的最短路能被更新，则图中有负环。复杂度为O(nm)。

bellman代码

#include<bits/stdc++.h>
using namespace std;
#define N 2000005
int t, n, m, ans=0, num, sum;
bool vis[N];
int  dis[N];
struct node {
	int head, to, tail;
}f[N];                    //结构体数组存边

void add(int a, int b, int c)  //这里需要判断边的正负，正负情况不同
{
	if (c >= 0)
	{
		f[++ans] = { a,b,c };      //注意这里没有使用链式前向星或者邻接表，就是单纯的存边
		f[++ans] = { b,a,c };
	}
	if (c < 0)
	{
		f[++ans] = { a,b,c };
	}
}

bool bellman()             //bellman核心代码段
{
	dis[1] = 0;
	for (int i = 2; i <= n; i++)    //初始化dis数组为无穷大
		dis[i] = 0x3f3f3f;
	for (int i = 1; i <= n - 1; i++) {  //只最多需要n-1次，这里可以优化
		for (int j = 1; j <= ans; j++) {
			int w = f[j].head, v = f[j].to;   //这里一定要加上对dis的特判，因为测试点中
			if (dis[v] > dis[w] + f[j].tail&&dis[w]!=0x3f3f3f) {   //有非联通图
				dis[v] = dis[w] + f[j].tail;
			}
		}
	}
	for (int k = 1; k <= ans; k++) {         //第n次更新，如果dis还在更新边，存在负环
		if (dis[f[k].head] == 0x3f3f3f || dis[f[k].to] == 0x3f3f3f)
			continue;
		if (dis[f[k].to] > dis[f[k].head] + f[k].tail)
			return true;
	}
	return false;
}
int main()
{
	cin >> t;
	while (t--) {
		memset(f, 0, sizeof(f));          //这里有多组数据，要清空
		cin >> n >> m;
		for (int i = 1; i <= m; i++) {
			int a, b, c;
			cin >> a >> b >> c;
			add(a, b, c);
		}
		if (bellman())              //判断条件
			cout << "YES" << endl;
		else
			cout << "NO" << endl;
	}
	return 0;
}

spfa解决思路：

spfa和bfs过程很相似，在spfa过程中一个点可以多次入队，更新距离，但是到某个点所更新的边最多有n-1个，即最坏的情况是一条直线，但如果更新的边的数量>=n，那么就说明存在负环，我们可以用一个数组ans，来存储到某个点所需要更新的边的数量，ans[1]=0，每次松弛时，我们使ans[y]=ans[x]+1;

spfa代码

#include<bits/stdc++.h>
using namespace std;
#define N 100005
int head[N], dis[N], ans[N];  //前面都是老伙计了，就不多介绍了
int t, n, m, cnt=1 , sum;
bool vis[N];
struct node {
	int to, tail, nx;
}f[N];

void add(int a, int b, int c)     //链式前向星存边
{
	f[cnt].to = b;
	f[cnt].tail = c;
	f[cnt].nx = head[a];
	head[a] = cnt++;
}

bool spfa()
{
	memset(dis, 0x3f, sizeof(dis));    //每次调用都有重新初始化
	memset(vis, 0, sizeof(vis));
	memset(ans, 0, sizeof(ans));
	queue<int>q;               //在函数体内定义，相当于每次进行清空
	q.push(1);
	dis[1] = 0;
	vis[1] = 1;       //这里出队后要回复vis，因为可能多次入队
	while (!q.empty()) {
		int x = q.front();
		q.pop();
		vis[x] = 0;
		for (int i = head[x]; i; i = f[i].nx) {  //这里应该比较熟悉吧，就是松弛操作
			int h = f[i].to;
			if (dis[h] > dis[x] + f[i].tail) {
				dis[h] = dis[x] + f[i].tail;
				ans[h] = ans[x] + 1;        //关键步骤，记录更新边的次数
				if (ans[h] >= n)         //存在负环
					return true;
				if (!vis[h]) {           //不在队列中，入队
					q.push(h);
					vis[h] = 1;
				}
			}
		}
	}
	return false;
}
int main()
{
	cin >> t;
	while (t--) {
		cin >> n >> m;
		cnt = 1;      //注意对于不同操作的链式前向星，cnt的初始化值不同，我这里是1
		memset(head, 0, sizeof(head));  //清空操作，多组数据
		for (int i = 1; i <= m; i++) {
			int a, b, c;
			cin >> a >> b >> c;
			add(a, b, c);
			if (c >= 0)         //特殊条件
				add(b, a, c);
		}
		if (spfa())
			cout << "YES" << endl;
		else
			cout << "NO" << endl;
	}
	return 0;
}

以上两种算法可以判断是否存在负环，根据需要合理的选择适合的算法。文章来源地址https://www.toymoban.com/news/detail-835062.html

到了这里，关于【模板】负环问题题解（spfa和bellman解决）的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！