关于深度学习和大模型的基础认知

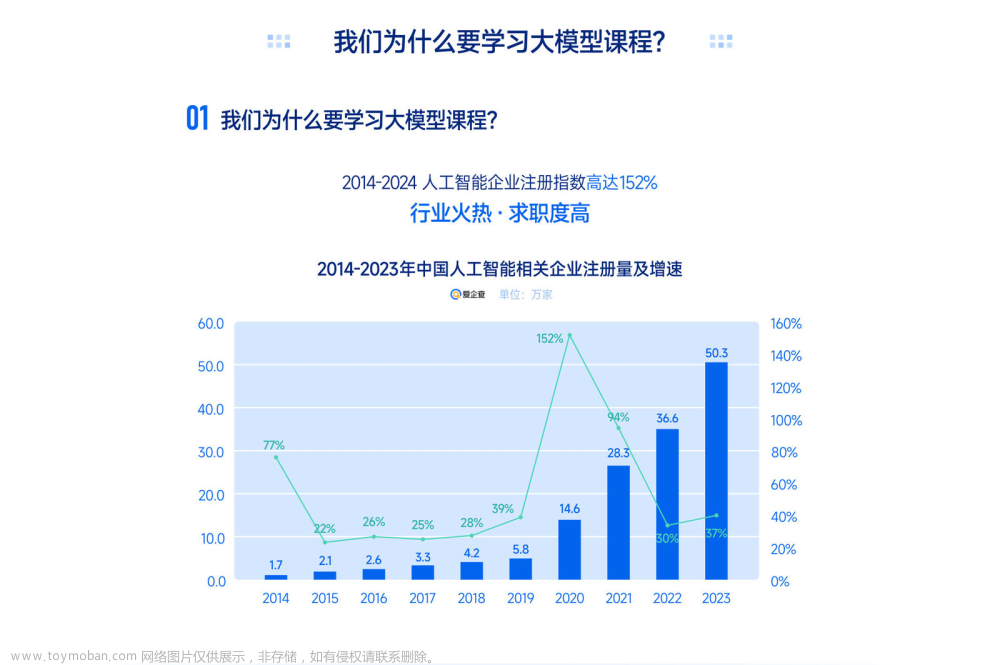
这年头，作为一个技术人，话头里没有“大模型”，和人聊天都聊不下去。为了让自己和大家能更好的参与话头，特撰写此文，提供一些对大模型的基础认知能力（门外汉，浅尝辄止）。旨在解自己的一些困惑，比如，模型是什么意思？千亿/万亿参数意味着什么？为什么大模型如此耗费算力？

什么是机器学习？

关于什么是机器学习，李宏毅老师在其课程中说地很精辟，即 机器学习 ≈ 机器自动找一个函数f( )

函数（function）就是一个输入，返回一个输出。数学表示是y=f(x)，x是自变量，y是因变量。比如一片面包的卡路里是200卡，那么我摄入的能量和面包数量（x）之间的关系就是函数 y = 200x，200是参数，有了这个函数，我就能“预测”如果我吃了3片面包，会摄入600卡能量。在机器学习领域，模型（model）和函数的意思等价，所谓大模型，就是一个巨大的函数。只不过这是一个上千亿参数，只有机器能处理和理解的巨大函数。

机器学习根据函数输出来分类：

1. 回归（Regression）：函数的输出是一个数值。比如通过今天的PM2.5，温度，预测明天的PM2.5

2. 分类（Classification）：函数的输出是一个类别（选择题）。比如判断一个邮件是不是spam（垃圾邮件）

3. 生成式学习（Generative Learning）：生成结构化文件（影像，语音，文句）

什么是深度学习？

我们以李宏毅老师课程中介绍的预测youtube频道观看人数为例。来介绍深度学习相关的概念。

这个案例是关于李宏毅老师的真实youtube频道，现在已知该频道2017~2020年3年每天观看人次的数据，现在我们需要通过机器学习帮我预测未来的观看人次。

最原始做法

机器学习就是找函数，假设这是一个线性函数 Y = b + wX，其中X是前一天的观看人次，Y是接下来一天的观看人次。b（bias，偏移量）和w（weight，权重）是未知参数（unknow paramters）。我们的目标就是b和w这两个未知参数求解出来，如何求解呢？

我们需要定义一个损失函数Loss function，它是关于b和w的函数L(b, w)。所谓损失就是计算值和标注值（正确数据）之间的差值。假设b,w的初始值分别是0.5k和1，那么L(0.5k, 1) = 标注的正确答案 — （0.5k + 1 * X）计算出来的答案。比如X代表2017/1/1的观看人数为4.8k，而2017/1/2的真实数据是4.9k（也叫label，标注值），根据我们设定的函数Y = b + wX，可以算出 0.5k + 1 * 4.8k = 5.3k。那么这里的损失，也叫误差（error）是e = 5.3k - 4.9k = 0.4k。

为了防止正负error不抵消，我们可以将误差定义为绝对值形式（Mean Absolute Error，MAE）。e = | y（函数值）— y（label值，真实数值）| ，这样对于总的Loss，我们可以定义为

了解了损失函数的意义，接下来的问题，就是找到一组b, w使得L(b, w)最小。寻找最小值，我们可以利用函数在切线方向斜率最大的特点，而函数的切线正是函数的导数（微分），这种利用微分寻找最优参数的过程，就是梯度下降方法（Gradient Descent）。

如下图所示，假设我们只看w（可以通过偏导数实现），那么L(b, w)将变成单变量函数，我们可以通过如下所示的梯度下降过程，找到那个使得L(b, w)最小的w（weight）值。类似的，我们可以找到使L(b, w)最小的b（bias）值。

通过对损失函数进行梯度下降方法，我们可以计算出当b=0.1k，w=0.97的时候损失函数L的值最小为0.48k。然而不幸的是在测试数据上的表现比较差，Loss是0.58k。所以总结一下机器学习主要就是三步：首先选择一个模型（线性模型，深度学习模型等），然后定义损失函数，最后求解最优参数值

多看几天的数据

聪明的你一定发现了，如果往前多参考几天的数据，而不仅仅是前一天的数据会不会更好呢。即我们的函数要改成：

假设我们要用前7天的数据，相对于前面的Y = b + wX函数，这个新函数无疑是更加复杂，同时，其未知参数也更加多，包括<b, w1, w2, w3, w4, w5, w6, w7>，这个更加复杂的算法带来的收益是我们的预测结果也将更加准确。通过同样的损失函数，经过梯度下降算法，我们得到θ为<0.05k 0.79 -0.31 0.12 -0.01 -0.10 0.30 0.18 >的时候，损失函数L( )最小为0.38k，在测试数据上的Loss是0.49K。看来用7个变量来代替1个变量，效果还是很明显的。

当我们继续加大参数量，从之前的7天数据，增加到28天，测试数据的Loss会更好一点，是0.46K。然而，在增加到56天时，Loss还是0.46K，就再也提升不上去了。想要提高成绩，我们需要更加复杂的模型。

线性模型太简单

Linear models  are too simple... we need more sophisticated models.

线性函数模型（Linear Model 比如 Y=b+wX）因为是直线，非常简单。不能模拟真实情况，真实的情况往往都不是简单线性关系，比如下图所示的红色曲线，是由三个折线组成。要拟合这样的折线，我们可以通过叠加多个sigmoid函数来达成。我们可以通过3个蓝色的sigmoid函数叠加来形成。

你也许会说，你这个还是折线，如果要表征更加平滑的曲线（Curve）怎么办呢？我们可以用多个分段的（piecewise）直线来模拟，只要线段足够多，就会足够接近。

在这个思路的引导下，我们可以将原来的简单线性函数，用一个更有弹性，可以模拟更复杂曲线的函数（多个sigmoid函数叠加）来取代：

如果需要看多天的数据，换成多个sigmoid的表达将如下所示：

深度学习

对于上面的新函数，假设我们选择3个特征（j: no. of features，也就是看过去3天的数据)，用3个sigmoid函数去逼近更复杂的函数（i：no. of sigmoid），那么sigmoid函数内部（蓝色虚线内）的计算式如下所示：

用线性代数的向量表示方法，可以改写为：

再加半部分的未知参数，完整的新函数可以表示为：

很明显，这个更复杂函数的参数比之前的linear model要多很多，在使用3个feature，3个sigmoid的情况下，参数数量是3*3 + 3 =9个，如果使用100个sigmoid函数呢？其未知参数将变成100*3+100=400个，这些参数在机器学习中统称为θ（theta），通常用向量表示。通过类似的Loss fucntion，以及梯度下降方法，我们可以找到使Loss最小的θ。

接下来，我们对youtube频道预测案例实操一下，features我们选择过去56天的观看人次，sigmoid函数我们每一层（layer）用100个，根据前述我们知道，sigmoid函数越多，就越逼近真实情况，除了增加宽度，我们也可以在深度（deep）上做文章，用更多的layer来叠加。实测结果如下：

这种有很多sigmoid函数叠加起来的函数模型，我们给他一个fancy name就是Deep learning。 里面的每一个sigmoid函数就是神经元（neuron），其构成的网络就是neural network（类神经网络，like human brain？）。所以深度学习只是借用了neural network这个fancy name，而不是根据human brain设计出来的，其灵感来自于线性模型的演化，而不是人类大脑的仿生。人类大脑只是一个形象的隐喻而已。

既然如此，是不是sigmoid越多越好，layer越深越好？实际上并非如此，当使用4个hidden layer的时候，虽然在训练数据上表现更好，但是测试数据的表现更差了，也就是发生了我们说的过拟合（overfitting）。

在做Deep learning训练的时候，会用到以下hyperparameters（超参数）：

• Batch size：对训练数据进行分批

• learning rate：这个是用梯度下降，找到使Loss function最小的b、w参数的学习率。Learning rate越大训练越快，但训练出的模型可能会越粗糙

• 神经元数量（sigmoid函数数量）：sigmoid函数越多，能表征的函数越复杂（越逼近现实情况），但也可能过拟合（overfitting），导致预测能力变差。

• hidden layer（隐藏层数）：层数越深，能表征的函数越复杂，但同样，过多layer可能overfiting

所以深度学习的参数数量 = 神经元数量 * 层数（hidden layer），比如有10个sigmoid函数，10层，那么需要训练的参数量就是100。1000亿大模型可能就是每一层有10亿个神经元，100层。

什么是LLM大语言模型？

大语言模型（LLM）是基于海量文本数据训练的深度学习模型。它不仅能够生成自然语言文本，还能够深入理解文本含义，处理各种自然语言任务，如文本摘要、问答、翻译等。2023年，参数量已从最初的十几亿跃升到如今的一万亿。参数量的提升使得模型能够更加精细地捕捉人类语言微妙之处，更加深入地理解人类语言的复杂性。

说到底，就是“大力出奇迹”，发生了量变到质变，上万亿参数的训练，需要巨大的计算资源，这个之前无法完成的计算量，随着计算机硬件的发展（英伟达为什么那么火）成为了可能。

为什么大模型需要大量的计算资源？

我们可以通过下面的方式，对大模型计算量进行估算。大模型训练都是用GPU，因为GPU的并行能力特别适合向量计算，衡量GPU性能的指标是FLOPS，全称是Floating-point Operations Per Second，即每秒浮点运算次数。

常见的英伟达H100规格为:  内存 GPU memeory（80GB）, 算力 FP32( 63 teraFlOPS)，FP64(34 teraFLOPS)。数据精度，有fp32和fp16两种，fp32是4Bytes（1.4*10^-45~1.7 * 10³⁸），fp16是2Bytes，大模型有很多层的矩阵乘法，0.1*0.1 .....0.1乘几十次，要保证精度不丢失的话最好是要fp32。

在训练大模型的时候，总算力需求 = 模型参数量 * 词数 * 单词运算量。以GPT3为例，其模型参数为总量为1750亿；GTP3的训练词为45TB，3000亿个单词。

关于单词运算量：

• • 推理：一个词更新一个参数，需要计算一次乘法，一次加法，2次运算/次。

  • 训练：涉及反向传播算法，是正向的2倍，故训练每个词的运算量是推理的3倍，需要消耗6次运算/次。

所以对于GPT3的训练来说，总算力需求 =1750亿 * 3000亿 * 6 = 3.15×10²³ FLOPS

GPU数量 = 总计算量 / GPU算力 * 利用率 / 计算用时

因此，如果ChatGPT一个月训练一次（一个月等于2592000秒），总计算量为3.15×10²³ FLOPS，一张H100 GPU单卡算力（63 TFLOPS）,其利用率为50%。所需的GPU数量为：

GPU数量 =  3.15×10²³ FLOPS / (6.3 ×10¹³ FLOPS ×50%) / 2.592 ×10 ⁶ = 3839

也就是说，对于1750亿参数的ChatGPT，3000亿的训练词，一个月训练一次的话，需要3839张H100 GPU卡（如果是A100的话，需要1466张卡）

对于推理，假设一个月的访问量是17.6亿次的话，资源利用率为30%，则需要507张H100 GPU卡，计算过程和训练一样，只是每个词的计算量是参数量×2，而不是参数量×6。

跑一下大模型，感受下计算量

这里我们选择的是microsoft开源的phi-2 transfomer模型，该模型是有27亿参数，用1.4T的tokens进行训练，使用96个A100-80G的显卡，训练了14天完成。据评测，其表现在130亿参数以下大模型中完胜。

接下来，我们可以按照以下步骤，在本地进行实践：

1. 准备Python虚环境

#创建并进入工作目录
cd D:\
mkdir transformers
cd transformers
 
#创建Python虚拟环境
python -m venv .env
 
#激活Python虚拟环境，注意：需管理员模式
.env\Scripts\activate
 
#升级pip
py -m pip install --upgrade pip

1. 安装Transforers

#安装Transformers和PyTorch
pip install 'transformers[torch]'

1. 配置环境变量

#设置Transformers离线运行
SET TRANSFORMERS_OFFLINE=1

1. 使用git下载模型。注意git版本必须要是2.43.0以上，否则不能下载4G以上的文件。phi-2模型文件超过4G

#切换至工作目录
cd D:\transformers

#下载模型
git clone https://huggingface.co/microsoft/phi-2

1. 运行代码，在D:\transformers 目录，添加一个新msphi2.py，添加以下代码，然后运行python .\msphi2.py

import torch
from transformers import AutoModelForCausalLM, AutoTokenizer

import time

class Timer:
    """用来记录执行时间的辅助类
    """
    _start_time = None
    _end_time = None

    @classmethod
    def start(cls, task):
        cls._start_time = time.time()
        print(f"开始{task}...")

    @classmethod
    def end(cls, task):
        cls._end_time = time.time()
        elapsed_time = cls._end_time - cls._start_time
        print(f"{task}用时 : {int(elapsed_time)}秒.")

Timer.start("加载")
# 加载模型
model = AutoModelForCausalLM.from_pretrained("./phi-2", torch_dtype=torch.float32, trust_remote_code=True)
tokenizer = AutoTokenizer.from_pretrained("./phi-2", trust_remote_code=True)
Timer.end("加载")

Timer.start("推理")
# 输入提示词
inputs = tokenizer('''Write a detailed analogy between mathematics and a lighthouse.''', return_tensors="pt", return_attention_mask=False)
# 进行推理
outputs = model.generate(**inputs, max_length=200)
text = tokenizer.batch_decode(outputs)[0]
# 输出推理结果
print(text)
Timer.end("推理")

我本地机器是8u16g的thinkpad，运行结果如下：

开始加载...
加载用时 : 21秒
开始推理...
Write a detailed analogy between mathematics and a lighthouse.
Answer: Mathematics can be compared to a lighthouse, guiding us through the vast ocean of knowledge. Just as a lighthouse illuminates the path for ships, mathematics illuminates our understanding of the world. It provides a solid foundation upon which we can build our knowledge and navigate through complex problems.
推理用时 : 98秒

当程序开始运行的时候，内存基本打满，CPU使用率也到了80%以上，即使这样对于200个tokens的输出还是需要98秒，可见用CPU跑大模型是一件多么不容易的事情。当我把max_length调整为100时，推理用时为49秒，时间也减少了一半。

最后，再次强调，本文只是对大模型，更多是对深度学习的基础认知。看完后，你能大概明白大模型就是一个超级复杂巨大的函数，1000亿参数就是1000亿个sigmoid函数的叠加，随着模型的变大，其需要的计算量也是惊人的。从而，在下次有人说谁谁谁又出了一个万亿参数的NB模型，我们能大概理解其为什么NB，万亿不再仅仅是一个空洞的数字。

参考：

李宏毅深度学习课程：https://www.youtube.com/watch?v=Ye018rCVvOo

梯度下降：https://www.jianshu.com/p/c7e642877b0e

phi-2模型：https://huggingface.co/microsoft/phi-2文章来源地址https://www.toymoban.com/news/detail-835102.html