BFS,DFS的应用场景及DFS的注意点，具体题：165.小猫爬山-Toy模板网

这篇具有很好参考价值的文章主要介绍了BFS,DFS的应用场景及DFS的注意点，具体题：165.小猫爬山。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

BFS,DFS的应用场景区别

具体题目来看:

DFS适合于“找出一条可行的路径(是否可到达问题)”，“要遍历所有点一遍”，“组合排列类问题”之类

BFS适合于“找最短路(权值为1)”，“层序遍历概念”

对于题目过程的感觉(我每次都是靠这个)

DFS对于数据像栈stack，后入栈的先出(从底层向上层回溯过程)，而BFS是直接借助了队列，先进先出；以后遇到搜索题目，想题目过程，是后进入的被删除，还是先进去的被删除，像stack还是queue。

//DFS模板
int dfs(int u)
{
    st[u] = true; // st[u] 表示点u已经被遍历过

    for (int i = h[u]; i != -1; i = ne[i])
    {
        int j = e[i];
        if (!st[j]) dfs(j);
    }
}

//BFS模板
queue<int> q;
st[1] = true; // 表示1号点已经被遍历过
q.push(1);

while (q.size())
{
    int t = q.front();
    q.pop();

    for (int i = h[t]; i != -1; i = ne[i])
    {
        int j = e[i];
        if (!st[j])
        {
            st[j] = true; // 表示点j已经被遍历过
            q.push(j);
        }
    }
}

当然，其实很多时候两个都可以，只是优化的问题。

DFS的注意点

顺序

用什么样的顺序去把题目所有可能不漏的暴搜一遍，正常从搜索树角度去分析会更有条理。

排列数字

常见的全排列顺序枚举（排列型枚举）所有可能；

BFS,DFS的应用场景及DFS的注意点，具体题：165.小猫爬山,搜索与图论,宽度优先,深度优先,算法,数据结构,图论,图搜索算法

指数型枚举所有可能，即考虑每个元素选与不选两种情况：

n皇后问题

枚举每个格子放与不放皇后，共个格子都这样

BFS,DFS的应用场景及DFS的注意点，具体题：165.小猫爬山,搜索与图论,宽度优先,深度优先,算法,数据结构,图论,图搜索算法

DFS什么时侯要回溯？(小猫爬山有具体题目分析)

DFS的本质就是在每一步做出不同选择，当这个选择可做可不做时，一般就要回溯。

因为选择选下了，会对后面的操作有影响(例：迷宫问题，你选择走（i,j）这步，再递归（i,j）四周作为下一步，而当这个系列的dfs走完了，你并没有清除查重数组st中的值，则后续这些点都无法在被遍历到了)。

回溯就是要消除搜索过程中不同可能性情况间的影响(迷宫问题：你走完（i，j）后，失败了，要把相关点的st数组清0，不要影响下一个情况走到这些点)

不需要回溯的常见情况：

当遇到一个选择，一定要对它操作时，就不需要回溯，例如要求所有格子的格子，要标记所有情况，找到一个点就要标记res++；如果取消标记，那么res会被重复计算。

例子：

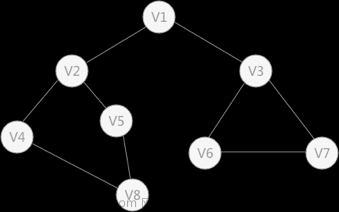
树图的标记问题：树的重心

排列数字：(如上图所示) 当你枚举第三位后，结果输出“1 2 3”，之后要回头找其他可能情况，先回溯到第二位,初始1在第一位(bool[1]=1)，而2已经枚举过了，所以枚举3，所以要在第三位回溯时，把3弃掉（bool[3]=0）;

DFS的优化剪枝(具体题目分析见下文：小猫爬山)

优化DFS时的搜索顺序：数据的顺序不同会对DFS的效率产生很大影响，原则是“大部分情况下，我们优先搜索分支较小的节点”
排除等效冗余：对于两个不同的状态，能够到达的搜索子树是等效的，那么一边就不走——注意这里不是“相同”而是“等效”，就算两个状态不同，如果它们对答案的影响都是相同的，就算作是“等效”的了。(实际上排除等效冗余就是提前预判是不是会产生重复)
可行性剪枝：当前选择违反题目条件/不可能到达答案，直接return结束
最优性剪枝：当前答案已经不优于现在的最优解，直接return结束
记忆化搜索：DP，换赛道了属于是。(~~选择DP，拥抱美好生活~~)

小猫爬山

BFS,DFS的应用场景及DFS的注意点，具体题：165.小猫爬山,搜索与图论,宽度优先,深度优先,算法,数据结构,图论,图搜索算法

本题有一种错误的贪心思想考虑：把猫猫按从小到大排序，再从小到大枚举小猫，尽可能把几个小的放在一个缆车里。

这样想太片面了，我们不是也可以把一个大的配一个小的吗？(例如：1，2，3，97，98，99情况。第一种考虑4辆，而第二种3辆)。

正确想法：

对于一只猫，要么和其他猫挤一辆车，要么自己坐一辆车，两种选择，用深度优先搜索。对于dfs函数种的变量(写我们关心的变量)：现在在考虑哪种小猫，已经租了几台缆车，每辆缆车上搭载小猫质量总和。

dfs(now,cnt)//now:第几只猫：cnt：已经用了几量车；num[i]：第i辆车上小猫质量和

1.和其他猫挤一辆车

枚举每个已有的缆车能否搭载小猫now：满足约束条件(now质量+num[i]<=缆车最大承重)，则小猫now放在缆车i上,在找dfs(now+1,cnt);小猫now在缆车i上情况结束要回溯到小猫now还没车放时状态，继续枚举已有的缆车；

2.自己坐一辆车

num[cnt+1]=小猫now的重量;//cnt+1即新的缆车；把小猫now放在缆车从cnt+1上，再dfs(now+1,cnt+1)//找小猫now+1要放的车，现在又cnt+1辆缆车了；最后小猫now放在cnt+1车的情况结束后，也要回溯，不回溯的话，此时的cnt+1这个车上永远有小猫now的重量，会对其他情况产生影响。

#include <algorithm>
#include <iostream>

using namespace std;

const int N = 2e1;

int cat[N], cab[N];
int n, w;
int ans;

bool cmp(int a, int b) {
    return a > b;
}

void dfs(int now, int cnt) {
    if (cnt >= ans) {//最优性剪枝
        return;
    }
    if (now == n + 1) {
        ans = min(ans, cnt);
        return;
    }
    //尝试分配到已经租用的缆车上
    for (int i = 1; i <= cnt; i++) {  //分配到已租用缆车
            //可行性剪枝
        if (cab[i] + cat[now] <= w) {
            cab[i] += cat[now];
            dfs(now + 1, cnt);
            cab[i] -= cat[now];  //还原
        }
    }

    // 新开一辆缆车
    cab[cnt + 1] = cat[now];
    dfs(now + 1, cnt + 1);
    cab[cnt + 1] = 0;
}

int main() {
    cin >> n >> w;
    for (int i = 1; i <= n; i++) {
        cin >> cat[i];
    }

    sort(cat + 1, cat + 1 + n, cmp);//优化搜索顺序 

    ans = n;

    dfs(1, 0);

    cout << ans << endl;

    return 0;
}