（9-8）基于深度强化学习的量化交易策略（OpenAI Baselines +FinRL+DRL+PyPortfolioOpt）：最小方差投资组合分配-Toy模板网

这篇具有很好参考价值的文章主要介绍了（9-8）基于深度强化学习的量化交易策略（OpenAI Baselines +FinRL+DRL+PyPortfolioOpt）：最小方差投资组合分配。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

1.1.11 最小方差投资组合分配

最小方差投资组合分配是一种通过优化投资组合权重，以最小化整个投资组合的方差（波动性）的方法。这种方法旨在构建一个投资组合，使其在给定一组资产的情况下，具有最小的风险。通过调整不同资产在投资组合中的权重，以达到整体风险最小化的目标，这种方法在现代投资组合理论中占有重要地位。

1. 优化投资组合

（1）PyPortfolioOpt 是一个Python库，用于进行投资组合优化和风险管理。提供了一组工具和方法，帮助用户根据给定的投资组合目标和限制找到最优的资产分配。使用以下命令安装PyPortfolioOpt库：

pip install PyPortfolioOpt

（2）下面这部分代码首先导入了EfficientFrontier和risk_models，这两个模块是PyPortfolioOpt库中用于投资组合优化和风险模型的关键组件。接着，从trade数据中提取了唯一的股票代号（unique_tic）和唯一的交易日期（unique_trade_date）。最后，打印了数据框（df）的前几行以进行预览。

from pypfopt.efficient_frontier import EfficientFrontier
from pypfopt import risk_models
unique_tic = trade.tic.unique()
unique_trade_date = trade.date.unique()
df.head()

执行后会输出：

	date	open	high	low	close	adjcp	volume	tic	day	macd	boll_ub	boll_lb	rsi_30	cci_30	dx_30	close_30_sma	close_60_sma	cov_list	return_list
0	2008-12-31	3.070357	3.133571	3.047857	3.048214	2.602662	607541200	AAPL	2	-0.097446	3.649552	2.895305	42.254771	-80.847207	16.129793	3.243631	3.375887	[[0.001348968986171653, 0.00042841264280825875...	tic AAPL AMGN AXP ...
1	2008-12-31	57.110001	58.220001	57.060001	57.750000	43.587837	6287200	AMGN	2	0.216368	58.947401	56.388599	51.060614	51.895357	10.432018	56.671334	56.044333	[[0.001348968986171653, 0.00042841264280825875...	tic AAPL AMGN AXP ...
2	2008-12-31	17.969999	18.750000	17.910000	18.549999	14.852879	9625600	AXP	2	-1.191668	23.723023	16.106977	42.521170	-74.811722	25.776759	20.030000	22.412000	[[0.001348968986171653, 0.00042841264280825875...	tic AAPL AMGN AXP ...
3	2008-12-31	41.590000	43.049999	41.500000	42.669998	32.005894	5443100	BA	2	-0.391219	42.894634	38.486366	47.290375	157.922391	5.366299	40.432000	43.304500	[[0.001348968986171653, 0.00042841264280825875...	tic AAPL AMGN AXP ...
4	2008-12-31	43.700001	45.099998	43.700001	44.669998	30.416977	6277400	CAT	2	0.979845	45.785565	38.404435	51.073052	98.904653	26.331746	40.266000	39.918333	[[0.001348968986171653, 0.00042841264280825875...	tic AAPL AMGN AXP ...

（3）下面的代码用于计算最小方差投资组合的资产价值。首先，为每个唯一的交易日期迭代，获取当天和下一天的数据。接着，计算收益率的协方差矩阵（Sigma）。随后，使用EfficientFrontier模块进行投资组合分配，设置权重的上下限为（0， 0.1），并通过min_volatility()方法获取最小方差投资组合的原始权重。清理这些权重后，计算当前资本、每个股票的当前投资金额、当前持有的股票数量，以及下一时间段的股票价格。最后，计算下一时间段的总账户价值，并在结果数据框中存储。

# 计算最小方差投资组合
portfolio = pd.DataFrame(index=range(1), columns=unique_trade_date)
initial_capital = 1000000
portfolio.loc[0, unique_trade_date[0]] = initial_capital

for i in range(len(unique_trade_date) - 1):
    # 获取当前日期和下一个日期的数据
    df_temp = df[df.date == unique_trade_date[i]].reset_index(drop=True)
    df_temp_next = df[df.date == unique_trade_date[i + 1]].reset_index(drop=True)
    # 计算协方差矩阵
    Sigma = df_temp.return_list[0].cov()
    # 配置投资组合
    ef_min_var = EfficientFrontier(None, Sigma, weight_bounds=(0, 0.1))
    # 最小方差投资组合
    raw_weights_min_var = ef_min_var.min_volatility()
    # 获取权重
    cleaned_weights_min_var = ef_min_var.clean_weights()
    # 当前资本
    cap = portfolio.iloc[0, i]
    # 每支股票的当前投资金额
    current_cash = [element * cap for element in list(cleaned_weights_min_var.values())]
    # 当前持有的股票数量
    current_shares = list(np.array(current_cash) / np.array(df_temp.close))
    # 下一时间段的股票价格
    next_price = np.array(df_temp_next.close)
    # 计算下一时间段的总账户价值
    portfolio.iloc[0, i + 1] = np.dot(current_shares, next_price)
# 转置数据框并设置列名
portfolio = portfolio.T
portfolio.columns = ['account_value']

portfolio.head()

执行后会输出：

account_value
2020-07-01 1000000
2020-07-02 1005234.883501
2020-07-06 1014933.780399
2020-07-07 1014238.666671
2020-07-08 1012674.038646

（4）计算使用A2C模型、最小方差投资组合以及基准（Dow Jones指数）的累积收益率，将每日收益率序列累积，得到了它们相对于初始值的总体增长情况，用于比较和评估不同投资策略的绩效。

a2c_cumpod =(df_daily_return.daily_return+1).cumprod()-1
min_var_cumpod =(portfolio.account_value.pct_change()+1).cumprod()-1
dji_cumpod =(baseline_returns+1).cumprod()-1

3. DRL、最小方差、DJIA的可视化

本项目使用Plotly库实现可视化，分别创建 DRL、最小方差和 DJIA 的可视化图。

（1）使用以下命令安装Plotly：

pip install plotly

（2）使用 Plotly 创建了多个散点图 (trace0_portfolio、trace1_portfolio、trace2_portfolio 等)，这些图分别表示 A2C 模型的投资组合收益、DJIA 收益以及最小方差投资组合的收益。通过将这些散点图组合在一起，并设置相应的日期和累积收益作为 x 和 y 轴，创建了一个可视化图表，用于比较这三个不同投资策略的表现。

from datetime import datetime as dt

import matplotlib.pyplot as plt
import plotly
import plotly.graph_objs as go
#%%
time_ind = pd.Series(df_daily_return.date)
#%%
trace0_portfolio = go.Scatter(x = time_ind, y = a2c_cumpod, mode = 'lines', name = 'A2C (Portfolio Allocation)')

trace1_portfolio = go.Scatter(x = time_ind, y = dji_cumpod, mode = 'lines', name = 'DJIA')
trace2_portfolio = go.Scatter(x = time_ind, y = min_var_cumpod, mode = 'lines', name = 'Min-Variance')
#trace3_portfolio = go.Scatter(x = time_ind, y = ddpg_cumpod, mode = 'lines', name = 'DDPG')
#trace4_portfolio = go.Scatter(x = time_ind, y = addpg_cumpod, mode = 'lines', name = 'Adaptive-DDPG')
#trace5_portfolio = go.Scatter(x = time_ind, y = min_cumpod, mode = 'lines', name = 'Min-Variance')

#trace4 = go.Scatter(x = time_ind, y = addpg_cumpod, mode = 'lines', name = 'Adaptive-DDPG')

#trace2 = go.Scatter(x = time_ind, y = portfolio_cost_minv, mode = 'lines', name = 'Min-Variance')
#trace3 = go.Scatter(x = time_ind, y = spx_value, mode = 'lines', name = 'SPX')

在上述代码中，trace0_portfolio 表示 A2C 模型的投资组合收益曲线，trace1_portfolio 表示 DJIA 的收益曲线，trace2_portfolio 表示最小方差投资组合的收益曲线。这个图表能够直观展示这三种策略在不同时间点的表现，帮助用户更好地理解它们的差异和优劣。

（2）使用 Plotly 创建了一个可视化图 (fig)，将之前定义的三个散点图 (trace0_portfolio、trace1_portfolio、trace2_portfolio) 添加到图表中，并进行一些布局的调整，以提高图表的可读性。

fig = go.Figure()
fig.add_trace(trace0_portfolio)
fig.add_trace(trace1_portfolio)
fig.add_trace(trace2_portfolio)

fig.update_layout(
    legend=dict(
        x=0,
        y=1,
        traceorder="normal",
        font=dict(
            family="sans-serif",
            size=15,
            color="black"
        ),
        bgcolor="White",
        bordercolor="white",
        borderwidth=2   
    ),
)
#fig.update_layout(legend_orientation="h")
fig.update_layout(title={
        #'text': "Cumulative Return using FinRL",
        'y':0.85,
        'x':0.5,
        'xanchor': 'center',
        'yanchor': 'top'})
#with Transaction cost
#fig.update_layout(title =  'Quarterly Trade Date')
fig.update_layout(
#    margin=dict(l=20, r=20, t=20, b=20),

    paper_bgcolor='rgba(1,1,0,0)',
    plot_bgcolor='rgba(1, 1, 0, 0)',
    #xaxis_title="Date",
    yaxis_title="Cumulative Return",
xaxis={'type': 'date', 
       'tick0': time_ind[0], 
        'tickmode': 'linear', 
       'dtick': 86400000.0 *80}

)
fig.update_xaxes(showline=True,linecolor='black',showgrid=True, gridwidth=1, gridcolor='LightSteelBlue',mirror=True)
fig.update_yaxes(showline=True,linecolor='black',showgrid=True, gridwidth=1, gridcolor='LightSteelBlue',mirror=True)
fig.update_yaxes(zeroline=True, zerolinewidth=1, zerolinecolor='LightSteelBlue')

fig.show()

在上述代码中，fig.add_trace 用于将每个散点图添加到可视化图中，fig.update_layout 用于设置可视化图的整体布局，包括标题、图例的位置和样式、背景色等。最后，通过 fig.show() 显示生成的可视化图。

整体而言，上述代码的功能是创建一个包含 A2C 模型投资组合收益、DJIA 收益和最小方差投资组合收益的可视化图，用于比较它们在累积收益方面的表现。如图9-8所示。

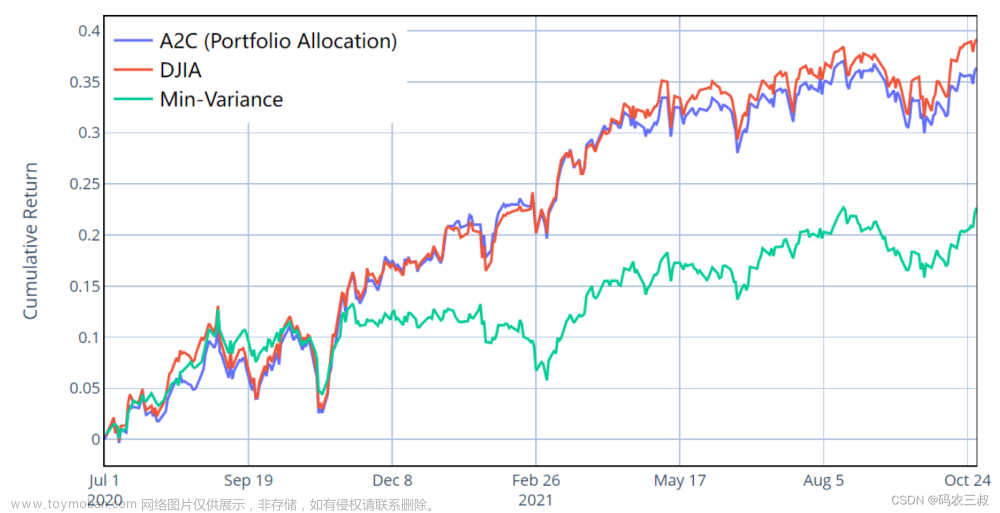
（9-8）基于深度强化学习的量化交易策略（OpenAI Baselines +FinRL+DRL+PyPortfolioOpt）：最小方差投资组合分配,金融大模型,人工智能,大数据,深度学习,算法,python,机器学习

图9-8 投资组合收益的可视化图

本项目已经完结：

（9-1）基于深度强化学习的量化交易策略（OpenAI Baselines +FinRL+DRL+PyPortfolioOpt）：背景介绍+项目目标+模块架构-CSDN博客

（9-2）基于深度强化学习的量化交易策略（OpenAI Baselines +FinRL+DRL+PyPortfolioOpt）：准备环境+下载数据-CSDN博客

（9-3）基于深度强化学习的量化交易策略（OpenAI Baselines +FinRL+DRL+PyPortfolioOpt）：数据预处理-CSDN博客

（9-4）基于深度强化学习的量化交易策略（OpenAI Baselines +FinRL+DRL+PyPortfolioOpt）：构建交易环境-CSDN博客

（9-5）基于深度强化学习的量化交易策略（OpenAI Baselines +FinRL+DRL+PyPortfolioOpt）：深度强化学习算法模型-CSDN博客

（9-6）基于深度强化学习的量化交易策略（OpenAI Baselines +FinRL+DRL+PyPortfolioOpt）：交易-CSDN博客

（9-7）基于深度强化学习的量化交易策略（OpenAI Baselines +FinRL+DRL+PyPortfolioOpt）：回测交易策略-CSDN博客文章来源地址https://www.toymoban.com/news/detail-835774.html

到了这里，关于（9-8）基于深度强化学习的量化交易策略（OpenAI Baselines +FinRL+DRL+PyPortfolioOpt）：最小方差投资组合分配的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！