机器学习——多元线性回归算法

9月前作者：debugBiubiubiu2000 分类：Toy博客阅读(48) 违法举报

这篇具有很好参考价值的文章主要介绍了机器学习——多元线性回归算法。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

多元线性回归算法

多元线性回归的概念

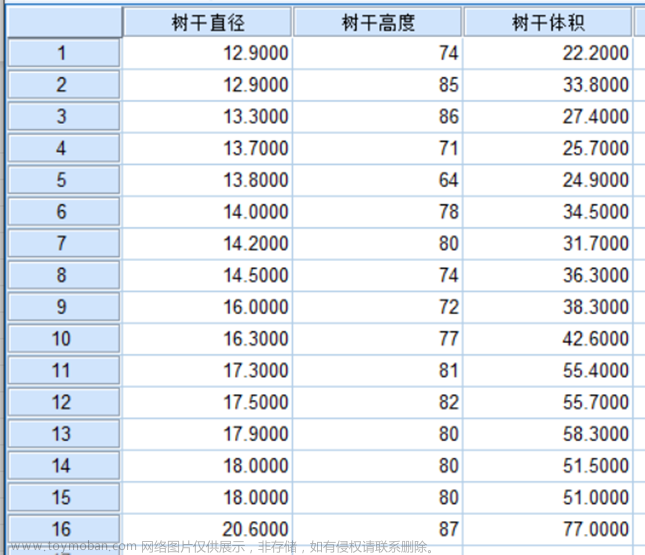
多元线性回归算法，即多特征量线性回归算法，用多个特征量来进行预测，如这里用多个特征量（房子面积、卧室数量、房屋楼层数、房子年龄）来预测房子的售价问题

机器学习——多元线性回归算法,机器学习,机器学习,线性回归,人工智能

多元线性回归的假设函数

用梯度下降算法处理多元线性回归参数

机器学习——多元线性回归算法,机器学习,机器学习,线性回归,人工智能

机器学习——多元线性回归算法,机器学习,机器学习,线性回归,人工智能

特征缩放

假如有一个多特征量的机器学习问题，并且这个问题中的多个特征可以在一个相近的范围内取值，那么可以采取特征缩放的方法，使得梯度下降算法更快收敛

举例来说，假设现在有一个具有两个特征的问题，其中特征一x1是房子面积，它的取值范围在0~2000之间，特征二x2是卧室数量，可能取值在1~5之间，特征缩放的做法如下

机器学习——多元线性回归算法,机器学习,机器学习,线性回归,人工智能

更一般地，执行特征缩放时，通常是将特征的取值约束到 -1~ +1的范围内，当然，不一定非得是[-1, 1]，是[-3, 3]，[-2, 3]这种和[-1, 1]范围差不多的就行，但是不能太大或者太小，否则就要进行缩放处理。所以当所有特征都在相近的取值范围内，梯度下降算法就会正常工作，得到正确的结果

机器学习——多元线性回归算法,机器学习,机器学习,线性回归,人工智能

除了将特征值除以最大值以外，还可以进行一个叫做均值归一化的处理

机器学习——多元线性回归算法,机器学习,机器学习,线性回归,人工智能

通过特征缩放，可以将梯度下降的速度变得更快，收敛所需的迭代次数更少

学习率α的选择

梯度下降算法如下，那么该如何选择学习率α呢？

机器学习——多元线性回归算法,机器学习,机器学习,线性回归,人工智能

我们可以通过J(θ)和梯度下降迭代次数的函数图像进行判断如何选择学习率

梯度下降算法正常工作的图像如下

机器学习——多元线性回归算法,机器学习,机器学习,线性回归,人工智能

学习率过大的函数图像

机器学习——多元线性回归算法,机器学习,机器学习,线性回归,人工智能

机器学习——多元线性回归算法,机器学习,机器学习,线性回归,人工智能综上，我们可以通过绘制J(θ)随迭代次数变化的函数图像，来判断我们所选择的学习率是否合适，一开始可以选择一个较小的学习率的值，然后绘制J(θ)随迭代次数变化的函数图像，根据函数图像对学习率做进一步的调整，不断尝试不同的学习率取值，直到最后取到合适的值。

多项式回归

直接看视频吧多项式回归文章来源地址https://www.toymoban.com/news/detail-836142.html

到了这里，关于机器学习——多元线性回归算法的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：如若内容造成侵权/违法违规/事实不符，请点击违法举报进行投诉反馈，一经查实，立即删除！

分享到：

领支付宝红包赞助服务器费用

【机器学习300问】11、多元线性回归模型和一元线性回归有什么不同？

在之前的文章中，我们已经学习了一元线性回归模型，其中最关键的参数是w和b。机器学习的目的就是去得到合适w和b后能准确预测未知数据。但现实世界是复杂的，一个事情的发生绝大多数时候不会是一个原因导致。因此多元线性回归模型区别与一元线

2024年01月22日
浏览(46)
【深入探究人工智能】逻辑函数|线性回归算法|SVM

🎉博客主页：小智_x0___0x_ 🎉欢迎关注：👍点赞🙌收藏✍️留言 🎉系列专栏：小智带你闲聊 🎉代码仓库：小智的代码仓库机器学习算法是一种基于数据和经验的算法，通过对大量数据的学习和分析，自动发现数据中的模式、规律和关联，并利用这些模式和规律来进行预测

2024年02月08日
浏览(62)
【机器学习界的“Hello World“ 】Logistic 分类回归算法（二元分类 & 多元分类）

🤵‍♂️ 个人主页: @计算机魔术师 👨‍💻 作者简介：CSDN内容合伙人，全栈领域优质创作者。该文章收录专栏 ✨— 机器学习 —✨ l o g i s t i c logistic l o g i s t i c （数理逻辑）回归算法(预测离散值 y y y 的非常常用的学习算法假设有如下的八个点( y = 1 或 0 ) y=1 或 0) y

2024年02月15日
浏览(44)
多元线性回归算法（matlab）

b：回归系数点估计 bint：回归系数区间估计 r:残差 rint:置信区间 stats:用于检验的统计量，有三个数值，相关系数r^2，F值，与F对应的概率p alpha:显著性水平(缺省时为0.05）说明：相关系数r^2越接近1，说明回归方程越显著； F越大，说明回归方程越显著与F对应的概率pa(显著性水

2024年02月07日
浏览(44)
多元线性回归算法（SPSS）

接上篇 (1条消息) 多元线性回归算法（matlab）_成、谋的博客-CSDN博客本篇博客主要参考自文章： (1条消息) 数学建模暑期集训6：用SPSS对数据进行多元线性回归分析_zstar-_的博客-CSDN博客_多元线性回归分析spss 三个变量：树干直径、树干高度、树干体积，树干体积和树干直径、

2023年04月20日
浏览(47)
【机器学习】十大算法之一 “线性回归”

作者主页：爱笑的男孩。的博客_CSDN博客-深度学习,活动,python领域博主爱笑的男孩。擅长深度学习,活动,python,等方面的知识,爱笑的男孩。关注算法,python,计算机视觉,图像处理,深度学习,pytorch,神经网络,opencv领域. https://blog.csdn.net/Code_and516?type=blog 个人简介：打工人。持续分

2024年02月09日
浏览(38)
解密人工智能：线性回归 | 逻辑回归 | SVM

前些天发现了一个巨牛的人工智能学习网站，通俗易懂，风趣幽默，忍不住分享一下给大家。点击跳转到网站。机器学习算法是一种基于数据和经验的算法，通过对大量数据的学习和分析，自动发现数据中的模式、规律和关联，并利用这些模式和规律来进行预测、分类或优化

2024年01月20日
浏览(54)
机器学习算法：线性回归、逻辑回归、决策树和随机森林解析

引言机器学习算法是人工智能领域的核心，它们用于解决各种问题，从预测房价到图像分类。本博客将深入探讨四种常见的机器学习算法：线性回归、逻辑回归、决策树和随机森林。线性回归什么是线性回归？线性回归是一种用于建立连续数值输出的机器学习模型的算法。

2024年02月10日
浏览(53)
学习记录2-多元线性回归模型（附上python代码)

研究货运总量 y （万吨）与工业总产值 x1（亿元）、农业总产值 x2（亿元）,居民非商品支出 X3 （亿元）的关系。数据见表3-9。 (1）计算出 y , x1 ,x2, x3 的相关系数矩阵。 (2）求 y 关于 x1 ,x2, x3 的三元线性回归方程。 (3）对所求得的方程做拟合优度检验。 (4）对回归方程做

2024年02月03日
浏览(43)
人工智能基础_机器学习003_有监督机器学习_sklearn中线性方程和正规方程的计算_使用sklearn解算八元一次方程---人工智能工作笔记0042

然后我们再来看看,如何使用sklearn,来进行正规方程的运算,当然这里首先要安装sklearn,这里如何安装sklearn就不说了,自己查一下首先我们还是来计算前面的八元一次方程的解,但是这次我们不用np.linalg.solve这个解线性方程的方式,也不用直接解正规方程的方式: 也就是上面这种

2024年02月08日
浏览(55)