一、 实验目的与要求
1.熟练掌握QR分解Gram–Schmidt方法;
2.掌握Householder方法;
3.能够判断矩阵是否可逆,并求出其逆矩阵。
二、 问题

三、模型建立及求解
1、Gram–Schmidt
1.1向量投影
向量的投影包含了两层意思:①正交关系:矢量与投影的差称为误差,误差和投影正交;②最短距离:投影空间中所有矢量中,与原矢量距离最近的,就是原矢量在该空间的投影,且最短距离的平方就是最小平方误差。
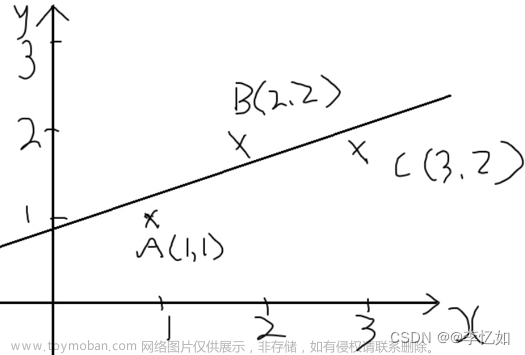
如图2所示,已知向量a和b,将b投影到a上,投影为p,设p=ta,t为常量,b与p的差为e,e=b-p。根据上述的正交关系e与p正交,根据最短距离有:。

设,则。令,求得。则,。当为单位向量,即时,有:
------(1.1.1)
------(1.1.2)
1.2 Gram–Schmidt正交化
Gram–Schmidt算法的目的是将给定的一组线性无关向量,转换为一组标准正交基。其主要思想为:每个新的矢量都减去它在已经正交化的矢量方向的投影,进而每次新增一个与所有已经正交化的矢量都正交的矢量。新的矢量只和之前的矢量有关,而与后面的矢量无关。每新增一个正交矢量,将其单位化,最终即可将一组线性无关向量转换成标准正交基。
如图3所示为将向量进行正交化过程。首先令,第一个矢量保持方向不变,将单位化得到;然后根据2.1式(1.1.1)和(1.1.2),令,可以保证与正交,将单位化得到。于是将向量正交化得到了标准正交基。

将向量的数目推广至n个,将正交化的过程为:
①令;
②正交化:根据公式计算;
③检验线性相关:若,则,是的线性组合,证明线性相关,退出迭代;否则进行下一步;
④单位化:令;
⑤重复步骤②~④,直至遍历完所有向量。
若在第i次迭代未退出,可证明与都是正交的:等式两边左乘,得:
(为常数可提到后面)
两两正交且都为单位向量,所以,且,
,所以:,即。因此,而方向与一致,故与都是正交的。通过上述过程可将n个线性无关的向量得到一组n维向量空间中的标准正交基。
1.3Gram–Schmidt算法QR分解
QR分解是将一个矩阵A分解成具有标准正交列向量的矩阵Q和上三角矩阵R(对角线元素不为0)的算法,即A=QR:
为A的列且线性独立,为Q的列且两两正交,所以有:
------(1.3.3)
Q矩阵可逆且其逆矩阵为,由于A=QR,所以。
矩阵Q的列由矩阵A的列通过Gram–Schmidt正交化得到。对A进行QR分解:A=QR。设为矩阵R的列,为R矩阵第i行第j列元素,则有:
在Gram–Schmidt正交化步骤中,新的矢量只和之前的矢量有关,而与后面的矢量无关。即只与和有关,而与无关,所以
,故R是上三角矩阵。
又而根据Gram–Schmidt正交化步骤, ,所以矩阵R对角线元素。
根据式(1.3.3),,有:
所以:
Gram–Schmidt算法实现矩阵A的QR分解为基于正交化定义的方法,实现核心类似数学归纳法,通过第k步的结果推导到第k+1步,逐列计算Q和R的元素,步骤如下:

1.4复杂度分析
设矩阵A大小为m×n,在第k次循环中,计算上三角非对角线元素的次数为k-1,每次内积的复杂度为2m-1 flops,总的复杂度为(k-1)(2m-1)flops;正交化复杂度为2(k-1)m flops;计算对角线元素和单位化的复杂度为3m flops。总计为(4m-1)(k-1)+3m flops。总共n次循环,总复杂度为:
flops。
1.5稳定性分析
导入附件MatrixA.mat中的矩阵进行QR分解后进行稳定性分析,验证得到的Q矩阵是否正交,通过计算与前面列之间的正交性的偏差:,当,说明Q矩阵的列不是完全正交的。
将计算结果画图显示,如图3所示。可以观察到,当k<35时,偏差值都为0,而后偏差急剧上升。分析原因,可能是由于浮点数存储的舍入误差,而每新增的正交向量都与前面的向量有关,即误差会累积。随着k增大超出一定范围后,误差累积量增加,导致波动性增大,Q矩阵逐渐失去正交性,稳定性降低。

由于Gram–Schmidt稳定性较低,下面将引入Gram–Schmidt的改进算法Modified Gram–Schmidt。
2、Modified Gram-Schmidt
2.1Modified Gram-Schmidt算法思想
由上述Gram-Schmidt算法的QR分解稳定性分析中可知,QR分解是逐列分解的,新向量只与前面的向量有关,与之后的向量无关。计算过程中由于浮点数计算精度问题会带来误差,而后面的向量只有在其被计算的时候才可见,这时误差可能已经积累到一定程度,故越往后计算误差越大,当矩阵维数较高的时候具有较差的稳定性。
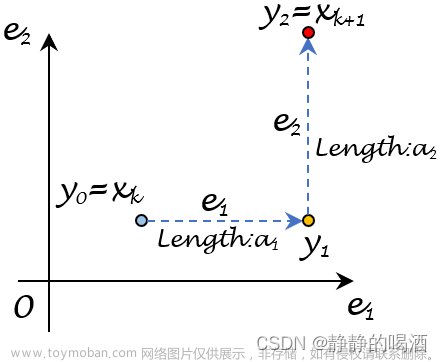
故想减小误差积累,提高稳定性,计算当前向量时同时考虑之后的向量。Modified Gram-Schmidt 的核心思想为:先选定一个向量作为第一个基准,然后将其余所有向量都投影到该基准的正交空间中,在该正交空间中,对剩下的向量重复前面的工作,最后所有的向量两两正交。实现步骤如下:

2.2复杂度分析
本质上Modified Gram-Schmidt 与Gran-Schmidt 是等价的,MGS只是对计算顺序进行了变更,计算次数不变,故算法复杂度依然为 flops。
2.3稳定性分析
导入附件MatrixA.mat中的矩阵进行QR分解后进行稳定性分析,计算并画出折线图,如图4所示,可以看到偏差的数量级为,相比于Gram-Schmidt方法 QR分解,稳定性有了极大提升。
分析该结果,Modified Gram-Schmidt 从开始就使所有的向量都参与计算,这样大部分的计算都在误差尚未积累到较大时就已经被执行。由于是按行计算R,MGS的计算量随循环次数逐步减少,因此前面积累的误差的影响就不会剧烈地扩散开,所以MGS可以使求得的矩阵Q的正交性更好,提高了稳定性。

3、Householder
3.1反射算子
设一个模为1的向量,令矩阵,则H为反射矩阵,也称为反射算子。反射矩阵是对称且正交的矩阵:
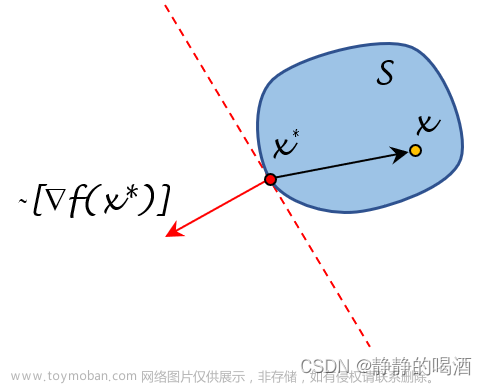
定义一个以为法向量的超平面S:。空间上任一向量x在S上的投影为:
x关于超平面S的对称点由其与反射算子的乘积给出:
3.2Householder算法QR分解
Householder算法实现QR分解的核心思想为,通过构造反射算子,逐列对原矩阵A进行Householder三角化,最终得到上三角矩阵R,而通过构造的反射算子计算出Q,实现QR分解。将一个3×3矩阵上三角化的过程下所示,、为构造的反射算子。
通过构造反射算子,逐列对矩阵进行Householder三角化的原理为:例如给定一个m×n的矩阵,首先对A的第一列进行上三角化时,需构造这样一个反射算子,使得,除第一个元素外全为0。相当于关于超平面对称的向量在一条坐标轴上,如图5所示。

实现了第一列的上三角化。
构造反射算子反射算子的过程为:对于第一列向量,定义函数,定义向量和:
为单位向量,反射算子使用构造:。
验证满足将A第一列上三角化的需求:将映射为:
而v满足:,所以:
所以满足要求。
当上三角化至进行至第k步时,矩阵具有如图6所示结构,空白处即和第i,j个位置的元素值为0。这时要第k列上三角化,相当于构造一个反射矩阵(长度为m-k+1,大小为(m-k+1)×(m-k+1)),对虚线包围区域的第一列上三角化,构造方式与上述矩阵A第一列类似。
得到后,利用构造一个如图7所示结构,仍是一个对称正交矩阵,即,。所得矩阵前k-1列不变,实现了对第k列的上三角化。

Householder算法实现过程如下所示:

至此,原矩阵A经过一系列变换得到上三角矩阵:。Householder方法实现的QR分解是对矩阵A计算一个完整的QR因数分解,而通常情况下不需计算矩阵。
的值通过计算得到:由于都为对称正交矩阵,故,令,则:
,
所以。
3.3复杂度分析
循环至第k次时复杂度为:
计算乘积:flops;
外积复杂度:flops;
减法次数:flops。
第k次循环总复杂度为:flops。算法总复杂度为:
flops
3.4稳定性分析
导入附件MatrixA.mat中的矩阵进行QR分解后进行稳定性分析,计算并画出折线图,如图8所示,可以看到偏差的数量级变成了,相比于MGS,稳定性有了极大提升。

4、QR分解应用
4.1求解线性方程组
使用QR分解求解线性方程组Ax=b,A大小为n×n,为非奇异矩阵。首先将矩阵A进行QR分解,A=QR,线性方程组变成QRx=b,所以。由于R为上三角矩阵,通过回代即可算出x。
复杂度分析:其中QR分解复杂度为,矩阵乘法为,回代为,所以平均复杂度约为flops。
导入实验1的A_b.mat文件,使用QR分解求解线性方程组。统计误差,与列主元消元法对比,如图9、图10所示。可以看到QR分解误差小于列主元消元法。

4.2求解逆矩阵
对于给定矩阵B,对其进行QR分解,若未能成功分解,即中途退出循环,证明B矩阵列向量线性相关,B为奇异矩阵;否则得到B=QR,求B的逆矩阵方法为:。
复杂度分析:其中QR分解复杂度为,求Q的转置为,由于R为上三角矩阵,求其逆的为,矩阵乘法为,所以平均复杂度约为
flops。
导入附件matrixB.mat给出的矩阵B,成功对其进行QR分解,证明B可逆。使用QR分解方法求其逆矩阵,计算与B相乘后每一列向量的二范数值,如图11所示,再验证对角线的元素值,如图12所示,可以看到所有的值都集中在1附近,正确求解出B的逆矩阵。文章来源:https://www.toymoban.com/news/detail-836320.html
 文章来源地址https://www.toymoban.com/news/detail-836320.html
文章来源地址https://www.toymoban.com/news/detail-836320.html
到了这里,关于最优化方法实验三--矩阵QR分解的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!