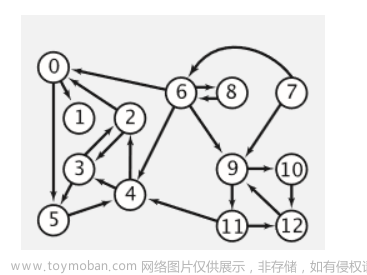
邻接表
有向图的邻接表是一种常用的表示方法,用于表示图中各个节点之间的关系。在有向图中,每条边都有一个方向,因此邻接表中的每个节点记录了该节点指向的其他节点。
具体来说,有向图的邻接表由一个由节点和它们的邻居节点列表组成的集合构成。对于每个节点,邻接表记录了该节点指向的所有邻居节点。这种表示方法可以用一个哈希表或数组来实现,其中哈希表或数组的键或索引表示节点,对应的值是一个列表,存储了该节点的所有邻居节点。
举例来说,考虑以下有向图:
A -> B, C
B -> C, D
C -> D
D -> A
对应的邻接表表示如下:
A: [B, C]
B: [C, D]
C: [D]
D: [A]
在邻接表中,每个节点及其邻居列表的组合表示了整个有向图的结构。使用邻接表可以有效地表示稀疏图,并且支持快速查找节点的邻居。
java表示这样的邻接表:
在 Java 中,可以使用 Map 来表示有向图的邻接表。具体来说,可以使用 Map<String, List>,其中键是节点的名称(如字符串表示),值是一个列表,存储了该节点指向的所有邻居节点的名称。以下是一个示例代码:
import java.util.*;
public class DirectedGraph {
private Map<String, List<String>> adjacencyList;
public DirectedGraph() {
this.adjacencyList = new HashMap<>();
}
public void addEdge(String source, String target) {
adjacencyList.computeIfAbsent(source, k -> new ArrayList<>()).add(target);
}
public List<String> getNeighbors(String node) {
return adjacencyList.getOrDefault(node, Collections.emptyList());
}
public static void main(String[] args) {
DirectedGraph graph = new DirectedGraph();
graph.addEdge("A", "B");
graph.addEdge("A", "C");
graph.addEdge("B", "C");
graph.addEdge("B", "D");
graph.addEdge("C", "D");
graph.addEdge("D", "A");
for (String node : graph.adjacencyList.keySet()) {
List<String> neighbors = graph.getNeighbors(node);
System.out.print(node + " -> ");
for (String neighbor : neighbors) {
System.out.print(neighbor + " ");
}
System.out.println();
}
}
}
}
在这个示例中,DirectedGraph 类表示有向图,使用 Map 存储邻接表。addEdge 方法用于添加一条边,getNeighbors 方法用于获取指定节点的邻居节点列表。在 main 方法中,创建了一个有向图并添加了一些边,然后遍历输出了每个节点及其邻居节点列表。
邻接矩阵
有向图的邻接矩阵是一个二维数组,用于表示图中节点之间的关系。对于有向图,邻接矩阵是一个 N × N 的矩阵,其中 N 是节点的数量,矩阵的每个元素 a[i][j] 表示从节点 i 到节点 j 是否存在一条有向边,通常用 0 或 1 表示不存在或存在边。
具体来说,邻接矩阵的构造如下:
如果图中存在一条从节点 i 到节点 j 的有向边,则将矩阵中的 a[i][j] 设为 1。
如果图中不存在从节点 i 到节点 j 的有向边,则将矩阵中的 a[i][j] 设为 0。
在有向图中,邻接矩阵是一个对称矩阵。但需要注意的是,有些情况下,如果图中存在权重(例如表示边的距离或成本),邻接矩阵的元素可能不只是 0 或 1,而是表示具体权重的数值。
举例来说,考虑以下有向图:
cssCopy code
A -> B
A -> C
B -> C
B -> D
C
C -> D
D
D -> A
对应的邻接矩阵为:
cssCopy code
A B C D
A 0 1 1 0
B 0 0 1 1
C
C 0 0 0 1
D
D 1 0 0 0
在 Java 中,可以使用二维数组来表示邻接矩阵,如下所示:
javaCopy code
int[][] adjacencyMatrix = {
{0, 1, 1, 0},
{0, 0, 1, 1},
{0, 0, 0, 1},
{1, 0, 0, 0}
}
};
其中,adjacencyMatrix[i][j] 表示从节点 i 到节点 j 是否存在一条有向边。
用 Java 代码表示有向图的邻接矩阵,你可以使用二维数组来实现。假设有 N 个节点,可以用一个 N × N 的二维数组来表示邻接矩阵,其中 adjMatrix[i][j] 表示从节点 i 到节点 j 是否存在一条有向边。如果存在,则 adjMatrix[i][j] 为 1;否则为 0。以下是一个示例代码:
javaCopy code
public class DirectedGraph {
private int[][] adjMatrix;
private int numNodes;
public DirectedGraph(int numNodes) {
this.numNodes = numNodes;
this.adjMatrix = new int[numNodes][numNodes];
}
public void addEdge(int source, int target) {
adjMatrix[source][target] = 1;
}
public void removeEdge(int source, int target) {
adjMatrix[source][target] = 0;
}
public boolean hasEdge(int source, int target) {
return adjMatrix[source][target] == 1;
}
public int getNumNodes() {
return numNodes;
}
public void printAdjMatrix() {
for (int i = 0; i < numNodes; i++) {
for (int j = 0; j < numNodes; j++) {
System.out.print(adjMatrix[i][j] + " ");
}
System.out.println();
}
}
public static void main(String[] args) {
DirectedGraph graph = new DirectedGraph(4);
graph.addEdge(0, 1);
graph.addEdge(0, 2);
graph.addEdge(1, 2);
graph.addEdge(1, 3);
graph.addEdge(2, 3);
graph.printAdjMatrix();
}
}
}文章来源:https://www.toymoban.com/news/detail-836813.html
在这个示例中,DirectedGraph 类表示有向图,使用二维数组 adjMatrix 来存储邻接矩阵。addEdge 方法用于添加一条边,removeEdge 方法用于删除一条边,hasEdge 方法用于判断两个节点之间是否有边。printAdjMatrix 方法用于打印邻接矩阵。在 main 方法中,创建了一个包含 4 个节点的有向图,并添加了一些边,然后打印了邻接矩阵。文章来源地址https://www.toymoban.com/news/detail-836813.html
到了这里,关于有向图的邻接表和邻接矩阵的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!