【数据结构】图的存储与遍历-Toy模板网

这篇具有很好参考价值的文章主要介绍了【数据结构】图的存储与遍历。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

图的概念

图是由顶点集合及顶点间的关系组成的一种数据结构：G = (V， E)

图分为有向图和无向图

在有向图中，顶点对<x, y>是有序的，顶点对<x，y>称为顶点x到顶点y的一条边(弧)，<x, y>和<y, x>是两条不同的边。
在无向图中，顶点对(x, y)是无序的，顶点对(x,y)称为顶点x和顶点y相关联的一条边，这条边没有特定方向，(x, y)和(y，x)是同一条边

【数据结构】图的存储与遍历,数据结构,数据结构,算法,图论

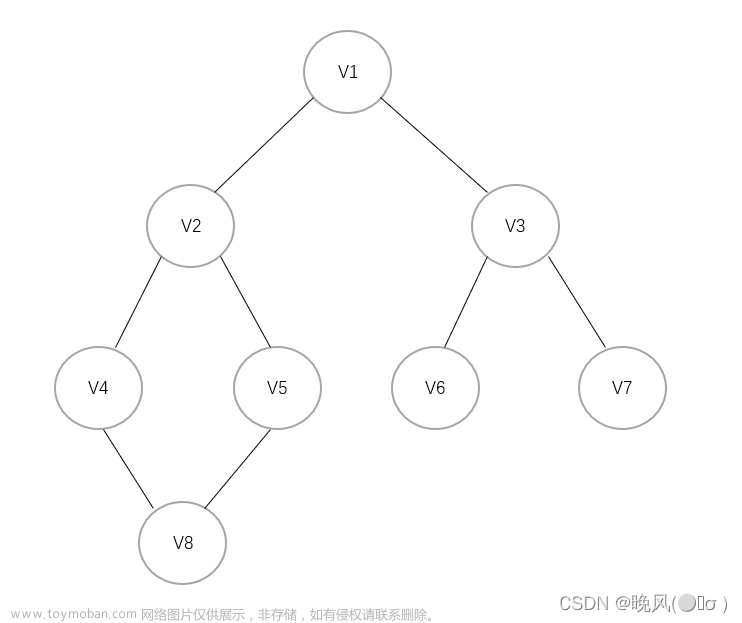
就像第一幅图中，<V1,V2>顶点构成有向图，边 E1和边E2是不同指向的

在第二幅图中，<V3,V4>构成无向图，E3就是连接二者关系的唯一边。

在生活中的关系，例如微信里的朋友关系就是无向的，只有双方都相连，才能发送消息

而类是与微博等就是单向的，你关注某人，就是一条边。当他也关注你时，才构成俩条边。

完全图

有n个顶点的无向图中，若有n * (n-1)/2条边，即任意两个顶点之间有且仅有一条边，
则称此图为无向完全图
在n个顶点的有向图中，若有n * (n-1)条边，即任意两个顶点之间有且仅有方向相反的边，则称此图为有向完全图

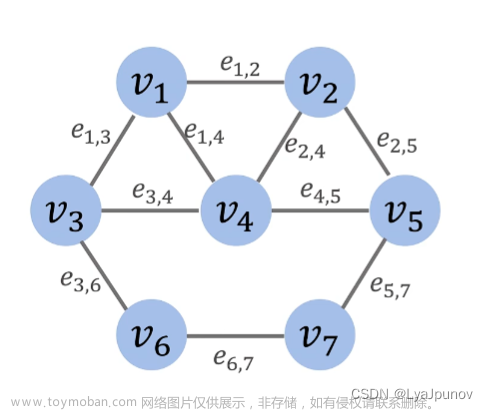
下列的图都是完全图

【数据结构】图的存储与遍历,数据结构,数据结构,算法,图论

邻接顶点

无向图中，v-u 称互为邻接顶点
有向图中，v->u 称u是v的邻接顶点

与顶点直接相邻的顶点

例如：G1中 0和2 都是 1的邻接顶点

0 1 2 3互为邻接顶点

图与树的主要联系与区别

树是一种特殊的图

图不一定是树

树关注结点的存值，图关注顶点和边的权值。

图的存储结构

本质就是将边和顶点，及其关系存储起来。

用vector数组保存顶点

vector<V> _vertexs;

利用map映射顶点和下标的关系

		map<V, int> _vIndexMap;

为了解决俩个顶点是否相连，相连的边权值是多少的问题。

解决方法主要有邻接矩阵，和邻接表

邻接矩阵

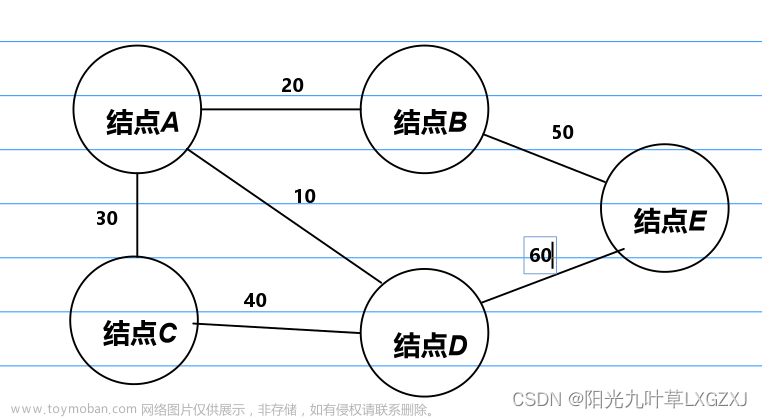
利用一个N*N的矩阵表示边和权值的关系

【数据结构】图的存储与遍历,数据结构,数据结构,算法,图论

如果想要找到顶点A相连的顶点，通过横行找到A，在通过纵行找到内容不为无穷大的 B D。

为了表示边权之间的关系，修改 0和1为权值w和无穷

规定顶点自己到自己是不相连，不连通为无穷。

【数据结构】图的存储与遍历,数据结构,数据结构,算法,图论

namespace Matrix
{
	template<class V, class W, W MAX_W = INT_MAX, bool Direction = false>
	class Graph
	{
		typedef Graph<V, W, MAX_W, Direction> Self;
	public:
		Graph()
		{

		}
		Graph(const V* a, size_t n)
		{
			_vertexs.reserve(n);
			for (size_t i = 0; i < n; i++)
			{
				_vertexs.push_back(a[i]);
				_vIndexMap[a[i]] = i;
			}
			_matrix.resize(n);
			for (size_t i = 0; i < _matrix.size(); i++)
			{
				_matrix[i].resize(n, MAX_W);
			}
		}

		//获取下标
		size_t GetVertexIndex(const V& v)
		{
			auto it = _vIndexMap.find(v);
			if (it != _vIndexMap.end())
			{
				return it->second;
			}
			else
			{
				throw invalid_argument("顶点不存在");
				assert(false);
				return -1;
			}
		}

		void _AddEdge(size_t srci, size_t dsti, const W& w)
		{
			_matrix[srci][dsti] = w;
			
			if (Direction == false)
			{
				_matrix[dsti][srci] = w;
			}
		}

		//添加边的关系
		void AddEdge(const V& src, const V& dst, const W& w)
		{
			size_t srci = GetVertexIndex(src);
			size_t dsti = GetVertexIndex(dst);
			_AddEdge(srci, dsti, w);
		}

	private:
		vector<V> _vertexs;               //顶点集合
		map<V, int> _vIndexMap;			  //顶点映射下标
		vector<vector<W>> _matrix;        //邻接矩阵
	};

关于图的构造，需要输入顶点，并且手动添加边。

添加边后，将邻接矩阵v->u的位置置为权值，如果是无向图，那么u->v也置上权值。

邻接矩阵的优缺点

邻接矩阵的存储方式非常适合稠密图
它能做到O(1)的效率判断俩个顶点的关系
不适合找出所有邻接的边

邻接表

邻接表：使用数组表示顶点的集合，使用链表表示边的关系
邻接表是指针数组，将所有邻接的边，都挂在vector下。

一般而言，邻接表有入边和出边，我们只关心出边。

【数据结构】图的存储与遍历,数据结构,数据结构,算法,图论

边的结构 dsti w next

【数据结构】图的存储与遍历,数据结构,数据结构,算法,图论

对于邻接表就是将有关联的边都挂载在数组上。

同样需要vector数组保存顶点，map保存顶点和下标的映射。

邻接表的内容是一个边结构，内容包含srci(不一定有)，dsti,w权值，next指向下一个关联的边。

namespace LinkTable
{
	template<class W>
	struct Edge
	{
		int _dsti;//目标点
		W _w; //权值
		Edge<W>* _next;
		Edge() = delete;

		Edge(int dsti,const W& w)
			:_dsti(dsti)
			,_w(w)
			,_next(nullptr)
		{
		}
	};
	template<class V, class W, bool Direction = false>
	class Graph
	{
		typedef Edge<W> Edge;
	public:
		Graph(const V* a, size_t n)
		{
			_vertexs.reserve(n);
			for (size_t i = 0; i < n; i++)
			{
				_vertexs.push_back(a[i]);
				_vIndexMap[a[i]] = i;
			}

			_tables.resize(n, nullptr);
		}

		//获取下标
		size_t GetVertexIndex(const V& v)
		{
			auto it = _vIndexMap.find(v);
			if (it != _vIndexMap.end())
			{
				return it->second;
			}
			else
			{
				throw invalid_argument("顶点不存在");
				assert(false);
				return -1;
			}
		}
		void _AddEdge(const size_t srci, const size_t dsti, const W& w)
		{
			//1->2
			Edge* eg = new Edge(dsti, w);
			eg->_next = _tables[srci];
			_tables[srci] = eg;
			
			//2->1
			if (Direction == false)
			{
				Edge* eg = new Edge(srci, w);
				eg->_next = _tables[dsti];
				_tables[dsti] = eg;
			}
		}

		void AddEdge(const V& src, const V& dst, const W& w)
		{
			size_t srci = GetVertexIndex(src);
			size_t dsti = GetVertexIndex(dst);
			_AddEdge(srci, dsti, w);
		}

		void Print()
		{
			//打印下标映射
			for (size_t i = 0; i < (_vertexs.size()); i++)
			{
				cout << "[" << i << "]" << "->" << _vertexs[i] << endl;
			}
			
			//打印边
			for (size_t i = 0; i < _tables.size(); i++)
			{
				cout << "[" << i << "]   ";
				Edge* cur = _tables[i];
				while (cur)
				{
					cout << "- [ dsti->" << cur->_dsti << "| w:"<<cur->_w<<"] -";
					cur = cur->_next;
				}
				cout << "null" << endl;
			}

		}
	private:
		vector<V> _vertexs;               //顶点集合
		map<V, int> _vIndexMap;			  //顶点映射下标
		vector<Edge*> _tables;         //邻接表（出边表）
	};

邻接表的优缺点

适合稠密图
适合找顶点出去的边
不适合用来确定俩个顶点的关系和权值

邻接矩阵和邻接表二者各有优势，相辅相成。在后续的最小生成树和最短路径中，邻接矩阵更方便

图的遍历

从v0出发，根据某种规则沿着图中各边访问图的顶点，每一个都会被访问到，且只被访问到一次。

遍历的方式分为广度优先BFS和深度优先DFS

广度优先BFS

广度优先类似于二叉树的层序遍历，从左到右依次遍历，一层到一层。

【数据结构】图的存储与遍历,数据结构,数据结构,算法,图论

BFS的思路

要实现层序遍历，就要维护一个队列，A出队列时候，带A的相邻B C D入队列
当 A 出完之后，B再出就会带A进，为了防止重复带入，再维护一张vector的数组，出过了就标记，只有当标记容器没有被标记时，才带进队列。

【数据结构】图的存储与遍历,数据结构,数据结构,算法,图论

		void BFS(const V& src)
		{
			size_t srci = GetVertexIndex(src);

			//队列和标记数组
			queue<int> q;
			vector<bool> visited(_vertexs.size(), false);

			q.push(srci);
			visited[srci] = true;
			
			while (!q.empty())
			{
				size_t front = q.front();
				q.pop();
				cout << front << ":" << _vertexs[front] << endl;
				for (size_t i = 0; i < _vertexs.size(); i++)
				{
					//入队列
					if (_matrix[front][i] != MAX_W)
					{
						if (visited[i] == false)
						{
							q.push(i);
							//修改标记
							visited[i] = true;
						}
					}
				}
			}
		}

【数据结构】图的存储与遍历,数据结构,数据结构,算法,图论

深度优先DFS

类似于二叉树的先序遍历，从上从往下，一直遍历到最深，知道遇到访问或结束，就返回。

【数据结构】图的存储与遍历,数据结构,数据结构,算法,图论

DFS需要一个起始点，标志从哪里开始遍历，需要一个visited数组，标记哪些顶点被访问过了

		void _DFS(size_t srci, vector<bool>& visited)
		{
			cout << srci << ":" << _vertexs[srci] << endl;
			visited[srci] = true;
			for (size_t i = 0; i < _vertexs.size(); i++)
			{
				if (_matrix[srci][i] != MAX_W && visited[i] == false)
				{
					_DFS(i, visited);
				}
			}
		}

		void DFS(const V& src)
		{
			size_t srci = GetVertexIndex(src);
			vector<bool>visited(_vertexs.size(), false);
			_DFS(srci, visited);
		}

【数据结构】图的存储与遍历,数据结构,数据结构,算法,图论