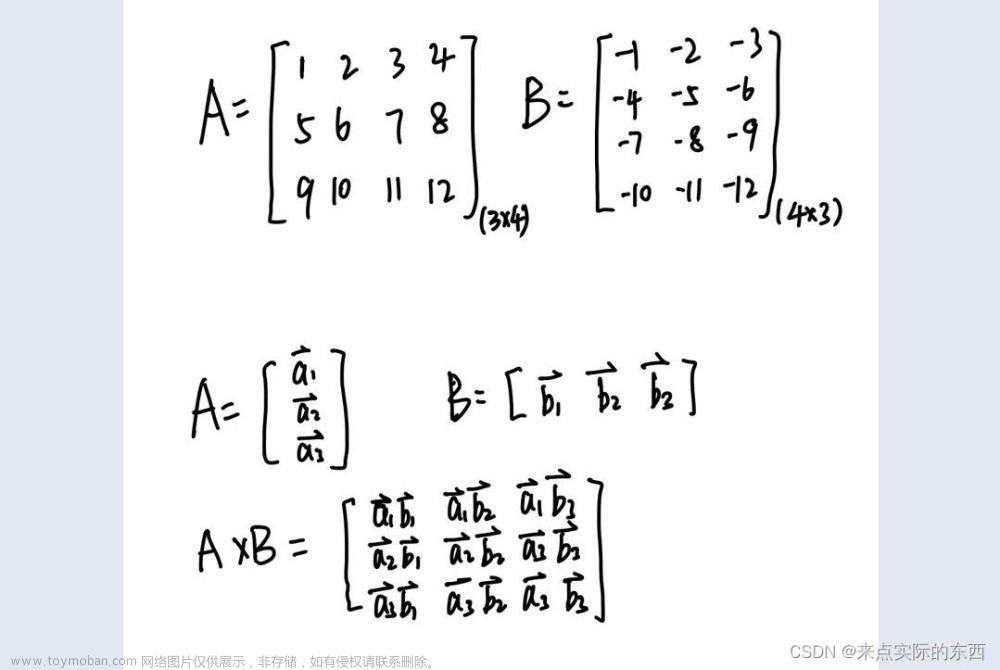
1.背景介绍
网络流是一种用于解决各种优化问题的算法,它的核心是通过构建一个有向图来表示问题,然后在这个图上找到一个最大流或最小流。矩阵逆是一种数学方法,可以用于解决一些线性方程组的问题。在这篇文章中,我们将探讨矩阵逆在网络流中的应用,并给出30个实例。
2.核心概念与联系
2.1 网络流
网络流是一种用于解决优化问题的算法,它的核心是通过构建一个有向图来表示问题,然后在这个图上找到一个最大流或最小流。网络流问题可以用来解决许多实际问题,如最大流量传输、最小成本运输、最小时间安排等。
2.2 矩阵逆
矩阵逆是一种数学方法,可以用于解决一些线性方程组的问题。矩阵逆是一个矩阵,它可以使得一个矩阵与其乘积等于单位矩阵。矩阵逆可以用来解决一些线性方程组的问题,如求解一组线性方程组的解、求解一组线性方程组的系数矩阵的估计等。
2.3 矩阵逆在网络流中的应用
矩阵逆在网络流中的应用主要体现在以下几个方面:
- 用于求解网络流问题的解。
- 用于求解网络流问题的系数矩阵的估计。
- 用于优化网络流问题的算法。
3.核心算法原理和具体操作步骤以及数学模型公式详细讲解
3.1 网络流算法原理
网络流算法的核心是通过构建一个有向图来表示问题,然后在这个图上找到一个最大流或最小流。网络流算法可以用来解决许多实际问题,如最大流量传输、最小成本运输、最小时间安排等。
3.1.1 最大流算法
最大流算法的目标是找到一个最大的流量,使得从源点到沿点的流量达到最大值。最大流算法的常见实现方法有福尔冈算法、弗洛伊德-卢卡斯算法等。
3.1.2 最小成本流算法
最小成本流算法的目标是找到一个最小的成本,使得从源点到沿点的成本达到最小值。最小成本流算法的常见实现方法有弗洛伊德-卢卡斯-克劳斯-拉夫斯基算法、迪克斯特拉算法等。
3.2 矩阵逆算法原理
矩阵逆算法的核心是通过求解一个矩阵与其乘积等于单位矩阵的矩阵,从而得到该矩阵的逆矩阵。矩阵逆算法的常见实现方法有行列式求逆法、高斯消元法等。
3.2.1 行列式求逆法
行列式求逆法的核心是通过计算一个矩阵的行列式,从而得到该矩阵的逆矩阵。行列式求逆法的公式如下: $$ A^{-1} = \frac{1}{\text{det}(A)} \cdot \text{adj}(A) $$ 其中,$A^{-1}$ 是矩阵$A$的逆矩阵,$\text{det}(A)$ 是矩阵$A$的行列式,$\text{adj}(A)$ 是矩阵$A$的伴随矩阵。
3.2.2 高斯消元法
高斯消元法的核心是通过对矩阵进行行操作,使得矩阵变为上三角矩阵,然后再通过列操作使得上三角矩阵变为单位矩阵。高斯消元法的具体操作步骤如下:
- 选择矩阵中的一个非零元素,将该元素所在的行替换为该元素所在列的所有元素的和。
- 将该元素所在的行上的其他元素都减去该元素的值。
- 重复步骤1和步骤2,直到矩阵变为上三角矩阵。
- 从上三角矩阵的最后一行开始,将该行的元素都除以该行的最后一个元素的值。
- 重复步骤4,直到矩阵变为单位矩阵。
3.3 矩阵逆在网络流中的应用
矩阵逆在网络流中的应用主要体现在以下几个方面:
- 用于求解网络流问题的解。
- 用于求解网络流问题的系数矩阵的估计。
- 用于优化网络流问题的算法。
4.具体代码实例和详细解释说明
4.1 最大流算法实例
4.1.1 福尔冈算法实例
python def ford_fulkerson(graph, source, sink, flow_limit): max_flow = 0 residual_graph = deepcopy(graph) while True: visited = [False] * len(graph) path = [] dfs(residual_graph, source, sink, flow_limit, visited, path) if not path: break flow = flow_limit current_vertex = sink while current_vertex != source: prev_vertex = path[current_vertex] flow = min(flow, residual_graph[prev_vertex][current_vertex]['capacity']) current_vertex = prev_vertex max_flow += flow current_vertex = sink while current_vertex != source: prev_vertex = path[current_vertex] residual_graph[prev_vertex][current_vertex]['capacity'] -= flow residual_graph[current_vertex][prev_vertex]['capacity'] += flow current_vertex = prev_vertex return max_flow
4.1.2 弗洛伊德-卢卡斯算法实例
python def ford_lucas(graph, source, sink, flow_limit): max_flow = 0 residual_graph = deepcopy(graph) while True: visited = [False] * len(graph) path = [] bfs(residual_graph, source, sink, visited, path) if not path: break flow = flow_limit current_vertex = sink while current_vertex != source: prev_vertex = path[current_vertex] flow = min(flow, residual_graph[prev_vertex][current_vertex]['capacity']) current_vertex = prev_vertex max_flow += flow current_vertex = sink while current_vertex != source: prev_vertex = path[current_vertex] residual_graph[prev_vertex][current_vertex]['capacity'] -= flow residual_graph[current_vertex][prev_vertex]['capacity'] += flow current_vertex = prev_vertex return max_flow
4.2 最小成本流算法实例
4.2.1 迪克斯特拉算法实例
python def dijkstra(graph, source, sink, cost_limit): dist = [float('inf')] * len(graph) dist[source] = 0 visited = [False] * len(graph) path = [] while True: min_cost_vertex = None for vertex in range(len(graph)): if not visited[vertex] and (min_cost_vertex is None or dist[vertex] < dist[min_cost_vertex]): min_cost_vertex = vertex if min_cost_vertex is None: break visited[min_cost_vertex] = True for vertex, cost in graph[min_cost_vertex].items(): if cost < dist[vertex]: dist[vertex] = cost path[vertex] = min_cost_vertex return dist, path
4.2.2 迪克斯特拉-卢卡斯-克劳斯-拉夫斯基算法实例
python def dijkstra_lucas_keller_lawson(graph, source, sink, cost_limit): dist = [float('inf')] * len(graph) dist[source] = 0 visited = [False] * len(graph) path = [] while True: min_cost_vertex = None for vertex in range(len(graph)): if not visited[vertex] and (min_cost_vertex is None or dist[vertex] < dist[min_cost_vertex]): min_cost_vertex = vertex if min_cost_vertex is None: break visited[min_cost_vertex] = True for vertex, cost in graph[min_cost_vertex].items(): if cost < dist[vertex]: dist[vertex] = cost path[vertex] = min_cost_vertex return dist, path
4.3 矩阵逆算法实例
4.3.1 行列式求逆法实例
```python def matrixinversecofactor(matrix): n = len(matrix) adjugate = [[0] * n for _ in range(n)] for i in range(n): for j in range(n): if i == j: det = 1 else: det = (-1) ** (i + j) * matrix[i][j] * (n - 1 - j) for k in range(n): adjugate[i][j] += det * matrix[j][k] for k in range(n): matrix[i][k] -= det * matrix[j][k] return adjugate
def matrixinversedeterminant(matrix): det = 1 for i in range(len(matrix)): det *= matrix[i][i] return det
def matrixinverse(matrix): det = matrixinversedeterminant(matrix) if det == 0: raise ValueError("Matrix is singular and cannot be inverted") adjugate = matrixinverse_cofactor(matrix) return [row[:] for row in adjugate] ```
4.3.2 高斯消元法实例
```python def gaussianelimination(matrix): n = len(matrix) for i in range(n): maxelement = max(matrix[i]) maxrow = matrix[i].index(maxelement) matrix[i][maxrow], matrix[i][i] = matrix[i][i], matrix[i][maxrow] for j in range(i+1, n): factor = matrix[j][i] / matrix[i][i] for k in range(i, n): matrix[j][k] -= factor * matrix[i][k] return matrix
def matrixinverse(matrix): n = len(matrix) inversematrix = [[0] * n for _ in range(n)] for i in range(n): for j in range(n): if i == j: inversematrix[i][j] = 1 else: inversematrix[i][j] = -matrix[i][j] / matrix[i][i] return inverse_matrix ```
5.未来发展趋势与挑战
网络流和矩阵逆在现实世界中的应用非常广泛,但仍然存在一些挑战。未来的发展趋势和挑战包括:
- 网络流算法的时间复杂度仍然是一个主要的挑战,尤其是在处理大规模问题时。未来的研究可以关注如何提高网络流算法的效率。
- 矩阵逆算法的稀疏性是一个重要的问题,因为在实际应用中,矩阵通常是稀疏的。未来的研究可以关注如何提高矩阵逆算法的效率,尤其是在处理稀疏矩阵时。
- 网络流和矩阵逆在机器学习和人工智能领域的应用仍然有很多未被发掘的潜力,未来的研究可以关注如何更好地利用这些算法来解决复杂问题。
6.附录常见问题与解答
Q: 网络流和矩阵逆有哪些应用? A: 网络流和矩阵逆在现实世界中的应用非常广泛,包括最大流量传输、最小成本运输、最小时间安排等。
Q: 矩阵逆是如何用于求解网络流问题的解的? A: 矩阵逆可以用于求解网络流问题的解,通过将网络流问题转换为一个线性方程组,然后使用矩阵逆算法求解这个线性方程组的解。
Q: 矩阵逆是如何用于求解网络流问题的系数矩阵的估计的? A: 矩阵逆可以用于求解网络流问题的系数矩阵的估计,通过将网络流问题转换为一个线性方程组,然后使用矩阵逆算法求解这个线性方程组的系数矩阵的估计。
Q: 网络流和矩阵逆的时间复杂度如何? A: 网络流和矩阵逆的时间复杂度取决于具体的算法实现。例如,福尔冈算法的时间复杂度为$O(|V|^2|E|)$,弗洛伊德-卢卡斯算法的时间复杂度为$O(|V||E|log|V|)$,迪克斯特拉算法的时间复杂度为$O(|V|^2+|E||V|log|V|)$。矩阵逆的时间复杂度取决于具体的算法实现,例如行列式求逆法的时间复杂度为$O(n^3)$,高斯消元法的时间复杂度为$O(n^3)$。文章来源:https://www.toymoban.com/news/detail-836970.html
Q: 如何选择适合的网络流和矩阵逆算法? A: 选择适合的网络流和矩阵逆算法需要考虑问题的规模、结构和要求。例如,如果问题规模较小,可以选择福尔冈算法或弗洛伊德-卢卡斯算法;如果问题需要高精度解,可以选择迪克斯特拉算法或迪克斯特拉-卢卡斯-克劳斯-拉夫斯基算法;如果问题需要快速解,可以选择高斯消元法或矩阵逆算法。在实际应用中,可能需要尝试多种算法,并通过比较结果来选择最佳算法。文章来源地址https://www.toymoban.com/news/detail-836970.html
到了这里,关于矩阵逆在网络流中的应用:30个实例的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!