【高级数据结构】Trie树

原理

介绍

高效地存储和查询字符串的数据结构。所以其重点在于：存储、查询两个操作。

存储操作

示例和图片来自：https://blog.csdn.net/qq_42024195/article/details/88364485

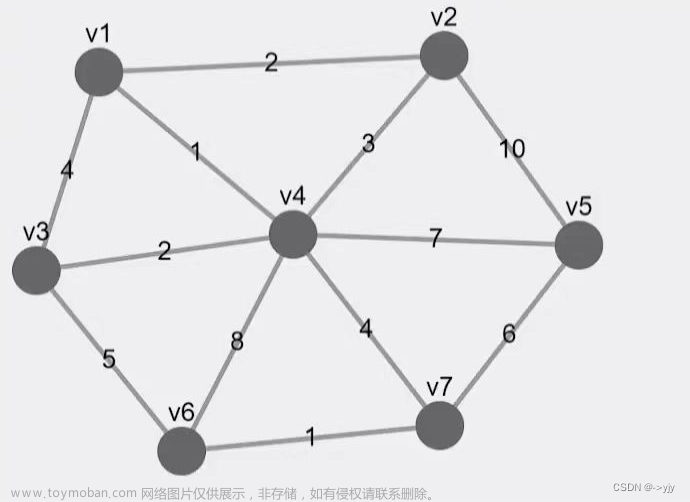
假设有这么几个字符串：b，abc，abd，bcd，abcd，efg，hii。最终存储出来的Trie图如下图所示：

具体是怎么存的呢？对于每一个字符串，从树的根节点开始，依次判断当前节点的儿子节点中是否有当前字符：

• 如果有，则进行下一个字符的判断，同时根节点更新为该儿子节点
• 如果没有，创建一个儿子节点为当前字符，然后根节点更新为该儿子节点

如果已经到了最后一个字符，就在对应的儿子节点进行一个标记，表示从根节点到该节点的字符组成的字符串是一个单词。（对应图中的红色部分）

查询

查询和存储的操作类似。对于一个给定的字符串，从树的根节点开始，依次判断当前节点的儿子节点中是否有当前字符：

• 如果有，则进行下一个字符的判断，同时根节点更新为该儿子节点
• 如果没有，则说明不存在该字符串，直接返回不存在

复杂度

时间复杂度：O(max_len(s))=O(h)，h为Trie树的高度，即最长字符串的长度。

空间复杂度：不超过O(N * max_len(s))。

代码实现

208. 实现 Trie (前缀树)

class Trie {

    private Trie[] children; // 当前节点的所有儿子
    private boolean isEnd; // 当前节点是否为一个单词的结尾

    public Trie() {
        children = new Trie[26]; // 假设字符串中都是小写字母，那么一个节点的所有儿子最多只有26个
        isEnd = false;
    }
    
    /**
		存储操作：插入一个字符串
	*/
    public void insert(String word) {
       Trie node = this; // 从根节点开始
        for(char c : word.toCharArray()) {
            int u = c - 'a'; // [a, z] -> [0, 25]
            if (node.children[u] == null) { // 当前节点node不存在儿子节点 
                node.children[u] = new Trie(); // 创建一个节点为当前字符
            } 
            node = node.children[u]; // 更新根节点为儿子节点
        }
        node.isEnd = true;
    }
    
	/**
		查询操作：查询某个字符串是否在树中。如果在树中，可以是树中单词的前缀，也可以是完整的单词
	*/
    private Trie searchPrefix(String prefix) {
        Trie node = this; // 从根节点开始
        for(char c : prefix.toCharArray()) {
            int u = c - 'a'; // [a, z] -> [0, 25]
            if (node.children[u] == null) { // 当前节点node不存在儿子节点 
                return null;
            } 
            node = node.children[u]; // 走到儿子节点
        }
        return node;
    }
    
    public boolean search(String word) {
    	// 查询树中是否存在完整的单词
        Trie node = searchPrefix(word);
        return node != null && node.isEnd;
    }
    
    public boolean startsWith(String prefix) {
    	// 查询树中是否存在某个前缀
        return searchPrefix(prefix) != null;
    }
}

/**
 * Your Trie object will be instantiated and called as such:
 * Trie obj = new Trie();
 * obj.insert(word);
 * boolean param_2 = obj.search(word);
 * boolean param_3 = obj.startsWith(prefix);
 */

当然，Trie树也可以查询存储并查询一个单词出现了几次，只需要把isEnd改成cnt就行。当cnt为0时，表示没出现过，即不是一个完整的单词；当cnt > 0时，表示出现过，cnt的大小即为出现的次数。文章来源地址https://www.toymoban.com/news/detail-837981.html

到了这里，关于【高级数据结构】Trie树的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！