引言
在计算机科学中,数据结构是组织和存储数据的基础框架,而算法则是处理这些数据的核心逻辑。在这众多的数据结构中,二叉树因其独特的层级结构、高效的搜索和插入操作,成为广泛应用的一种非线性数据结构。本文将深入探讨二叉树的定义、种类、操作方法以及实际应用场景。
一、什么是二叉树?
二叉树(Binary Tree) 是一种每个节点最多有两个子节点的树形数据结构。它具有根节点、叶子节点和内部节点的概念,其中:
- 根节点是没有父节点的节点。
- 叶子节点是没有任何子节点的节点。
- 内部节点既有左子节点也有右子节点。
二、二叉树的种类及特点
-
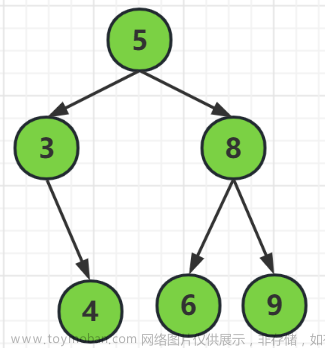
二叉查找树(Binary Search Tree, BST):每个节点的左子树中的所有节点的值都小于该节点,而其右子树中所有节点的值都大于该节点。这种特性使得BST在进行查找、插入和删除操作时,时间复杂度可达到O(log n)。
-
完全二叉树(Complete Binary Tree):除了最后一层外,每一层的节点数都达到最大,并且最后一层的节点都尽可能地集中在左边。
-
满二叉树(Full Binary Tree):所有层的节点数都达到最大,即除了叶子节点外,每个节点都有两个子节点。
-
平衡二叉树(Balanced Binary Tree):左右两个子树的高度差不超过1,如AVL树和红黑树。这类二叉树保证了查找等操作的时间复杂度始终为O(log n),极大地提高了效率。
三、二叉树的基本操作
-
创建二叉树:从根节点开始,递归地或迭代地添加节点至合适的位置。
-
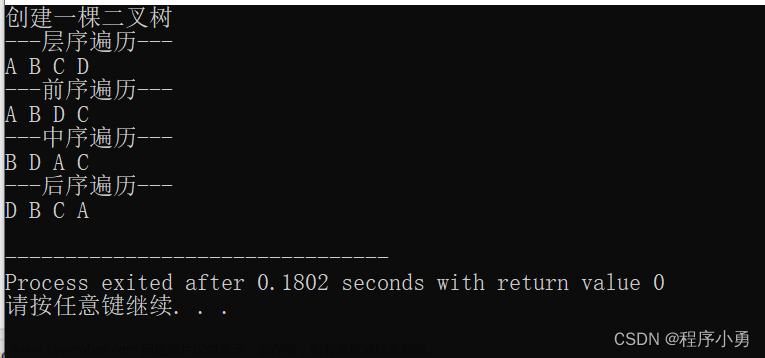
遍历二叉树:常见的遍历方式有前序遍历(根-左-右)、中序遍历(左-根-右)、后序遍历(左-右-根)和层次遍历(按层次从上到下、从左到右)。
-
查找节点:根据二叉查找树的性质,在BST中可以通过比较目标值与当前节点值来确定向左还是向右子树继续查找。
-
插入节点:在合适的子树位置创建新节点,保持BST的性质不变。
-
删除节点:针对不同情况(无子节点、仅有一个子节点或有两个子节点),采用不同的策略移除节点并调整树结构。
四、二叉树的实际应用
二叉树广泛应用于软件开发和计算机科学领域,包括但不限于:
-
数据库索引:B树和B+树作为特殊的平衡二叉树,常用于数据库系统建立索引以提高查询速度。
-
文件系统:NTFS等现代文件系统使用类似于B+树的结构管理目录和文件。
-
编译器:词法分析阶段利用二叉树实现符号表;语法分析阶段构建抽象语法树(AST)。
-
图形学:场景图、渲染队列等常常采用树状结构表示。
-
动态规划问题:一些动态规划问题可以借助二叉树来优化求解过程,例如斐波那契数列可以用记忆化搜索结合二叉树进行高效计算。
五、二叉树的代码实践
1.节点类
class HeroNode {
private int no;
private String name;
private HeroNode lift;
private HeroNode right;
public HeroNode(int no, String name) {
this.no = no;
this.name = name;
}
public int getNo() {
return no;
}
public void setNo(int no) {
this.no = no;
}
public String getName() {
return name;
}
public void setName(String name) {
this.name = name;
}
public HeroNode getLift() {
return lift;
}
public void setLift(HeroNode lift) {
this.lift = lift;
}
public HeroNode getRight() {
return right;
}
public void setRight(HeroNode right) {
this.right = right;
}
@Override
public String toString() {
return "HeroNode{" +
"no=" + no +
", name='" + name + '\'' +
'}';
}
}2.前序遍历
// 编写前序遍历方法
// 思路
// 1.前序的顺序是 根左右
// 2.先输出根节点
// 3.左节点不为空递归向左子树前序遍历
// 4.右节点不为空递归向右子树前序遍历
public void preOrder() {
System.out.println(this);
if (this.lift != null) {
this.lift.preOrder();
}
if (this.right != null) {
this.right.preOrder();
}
}3.中序遍历
// 中序遍历
// 思路
// 1.中序的顺序是 左根右
// 2.左节点不为空递归中序遍历
// 3.输出当前节点
// 4.右节点不为空递归向右子树中序遍历
public void infixOrder() {
if (this.lift != null) {
this.lift.infixOrder();
}
System.out.println(this);
if (this.right != null) {
this.right.infixOrder();
}
}4.后序遍历
// 后序遍历
// 思路
// 1. 后序的顺序是 左右跟
// 2.左节点不为空递归后序遍历
// 3.右节点不为空递归向右子树后序遍历
// 4.输出当前节点
public void postOrder() {
if (this.lift != null) {
lift.postOrder();
}
if (this.right != null) {
this.right.postOrder();
}
System.out.println(this);
}5.先序遍历查找
// 前序遍历查找
// 思路
// 1.先比较当前节点的编号是否和查找值编号相同,相同直接返回当前节点,不相同向左递归查找
// 2.左子节点不为空,向左递归查找,若找到则返回当前节点否则向右递归查找
// 3.右子节点不为空,向右递归查找,若找到则返回当前节点否则返回空
public HeroNode preOrderSearch(int heroNo) {
if (this.no == heroNo) {
return this;
}
HeroNode heroNode = null;
if (this.lift != null) {
heroNode = this.lift.preOrderSearch(heroNo);
}
if (heroNode != null) {
return heroNode;
}
if (this.right != null) {
heroNode = this.right.preOrderSearch(heroNo);
}
return heroNode;
}6.中序遍历查找
// 中序遍历查找
// 思路
// 1.左子节点不为空,向左递归查找,若找到则返回当前节点否则比较当前节点
// 2.比较当前节点的编号是否和查找值编号相同,相同直接返回当前节点,不相同向右递归查找
// 3.右子节点不为空,向右递归查找,若找到则返回当前节点否则返回空
public HeroNode infixOrderSearch(int heroNo) {
HeroNode heroNode = null;
if (this.lift != null) {
heroNode = this.lift.infixOrderSearch(heroNo);
}
if (heroNode != null) {
return heroNode;
}
if (this.no == heroNo) {
return this;
}
if (this.right != null) {
heroNode = this.right.infixOrderSearch(heroNo);
}
return heroNode;
}7.后序遍历查找
// 后序遍历查找
// 思路
// 1.左子节点不为空,向左递归查找,若找到则返回当前节点否则向右递归查找
// 2.右子节点不为空,向右递归查找,若找到则返回当前节点否则比较当前节点
// 3.比较当前节点的编号是否和查找值编号相同,相同直接返回当前节点,不相同返回null
public HeroNode postOrderSearch(int heroNo) {
HeroNode heroNode = null;
if (this.lift != null) {
heroNode = this.lift.postOrderSearch(heroNo);
}
if (heroNode != null) {
return heroNode;
}
if (this.right != null) {
heroNode = this.right.postOrderSearch(heroNo);
}
if (heroNode != null) {
return heroNode;
}
if (this.no == heroNo) {
return this;
}
return heroNode;
}8.二叉树类遍历查找方法
//二叉树类
class BinaryTree {
HeroNode root;
public void setRoot(HeroNode root) {
this.root = root;
}
//前序遍历
public void preOrder() {
if (this.root != null) {
this.root.preOrder();
} else {
System.out.println("该二叉树为空!!!");
}
}
// 中序遍历
public void infixOrder() {
if (this.root != null) {
this.root.infixOrder();
} else {
System.out.println("该二叉树为空!!!");
}
}
// 后序遍历
public void postOrder() {
if (this.root != null) {
this.root.postOrder();
} else {
System.out.println("该二叉树为空!!!");
}
}
// 先序遍历
public HeroNode preOrderSearch(int heroNo) {
if (this.root != null) {
return this.root.preOrderSearch(heroNo);
} else {
return null;
}
}
// 中序遍历
public HeroNode infixOrderSearch(int heroNo) {
if (this.root != null) {
return this.root.infixOrderSearch(heroNo);
} else {
return null;
}
}
// 后序遍历
public HeroNode postOrderSearch(int heroNo) {
if (this.root != null) {
return this.root.postOrderSearch(heroNo);
} else {
return null;
}
}
}文章来源:https://www.toymoban.com/news/detail-838004.html
六、总结
二叉树作为基础而又灵活的数据结构,其多样化的形态和丰富的操作方法使其在实际工程应用中占据重要地位。掌握二叉树的原理和实现不仅可以提升编程能力,而且有助于理解更复杂的算法设计和数据结构优化。在不断探索和实践中,我们能够更加深刻地领略到数据结构与算法的魅力,并在实际项目中发挥关键作用。文章来源地址https://www.toymoban.com/news/detail-838004.html
到了这里,关于数据结构与算法-二叉树的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!