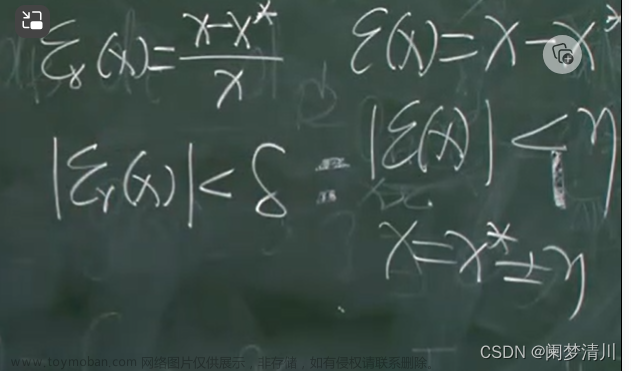
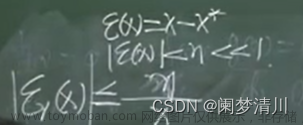
绝对误差:精确值-近似值;
举个例子:从A到B,应该有73千米,但是我们近似成了70千米;从C到D,应该是1373千米,我们近似成了1370千米,如果使用绝对误差,结果都是3,显然无法衡量我们误差的大小,这个时候我们引入了相对误差;
相对误差:精确值-近似值/精确值;我们希望通过两者的界限可以相互转换,所以我们在实际计算时候,用绝对误差除以近似值就得到相对误差,这个时候如果我们知道绝对误差的界限,我们就可以得出相对误差的界限(通过证明可以利用无穷小得知,这样替换以后得到的相对误差会更小);
误差的种类:
(1)模型误差:就是建立模型时候,忽略掉的因素,比如自由落体的问题,我们忽略空气阻力建立的数学模型,这个过程所产生的误差就是模型误差;
(2)观测误差:那自由落体问题,计算下落时间,物体到地面的高度会有观测误差;
(3)方法误差:一个实际问题会有不同的解决方案,我们利用不同的方案,就会得到不同的精度,这个过程的误差叫做方法误差;
(4)舍入误差:就是由于计算机的四舍五入而产生的误差,我本来也是认为计算机不会四舍五入,老师讲解后才明白计算机的精度是有限的,当我们的计算超过计算机的精度的时候,计算机无法准确的计算,它会根据实际情况取舍,例如,有一个0~1之间数字超过计算机的精度,如果距离0更近,就按照0进行计算,否则就按照1进行计算;减小舍入误差的方法就是减少计算的时间,步骤;
误差的传播:
这里老师引入了一个误差传播系数的概念,通过它衡量单个误差对于结果误差的影响;
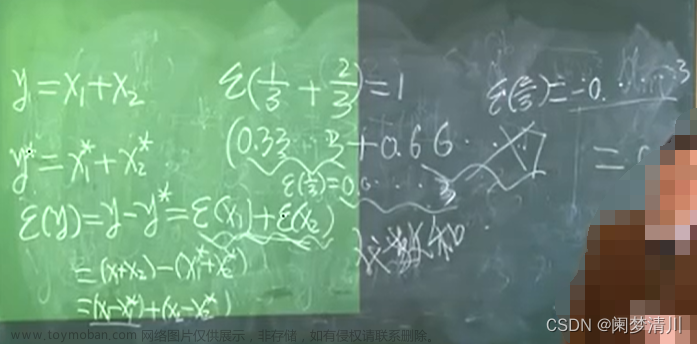
(1)加法:
例如1/3+2/3=1;其实计算机在进行计算时候,是进行了四舍五入的,因为1/3和2/3都无法精确地进行计算,这个时候1/3的误差是0.000.........3(因为真实值是无限无数的3,但是计算机只是取了有限位数;2/3再进行计算时误差是-0.0000.......3(因为真实值是无限位数的6,但是计算机取大了,误差是精确值减去近似值,所以是一个负数)两者在相加的过程中是完全抵消掉的,所以我们依然可以得出正确的答案;这里y的绝对误差是两者的代数和,是带有正负号的;所以两者相加时候,误差不一定会增加;
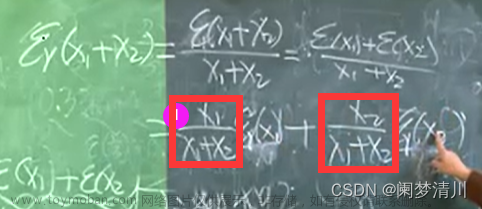
这里的系数就是误差传播系数,通过它来衡量单个误差对于结果误差的影响程度,通过放缩法可以得到相对误差一定是减小了的;
(2)减法:
同理可得,做减法的时候,当x1,x2很接近的时候,就会得到误差传播系数无穷大,扩大误差,因此,减小误差的手段就是避免两个十分相近的数字进行减法;两个相近的近似数做减法才有很大误差;
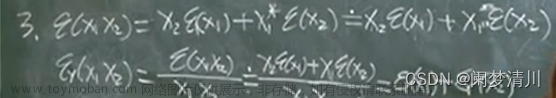
(3)乘法:
显而易见,X1的传播系数是X2,X2的误差传播系数是X1;因此减小乘法运算的误差就要避免2个绝对值很大的数字相乘;而相对误差是两个相对误差的代数和

(4)除法:
根据通式,分别对x1,x2求偏导数,减小误差的方法就是避免绝对值很小的数字做除法运算,通过凑配得出相对误差
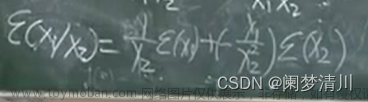

算法的稳定性,收敛性:当我们计算第无穷项数之后,误差趋近于0时,我们称该算法是收敛的;文章来源:https://www.toymoban.com/news/detail-838198.html
当输入的误差越小时候,输出的误差越小,我们称该算法是可控的,稳定的。文章来源地址https://www.toymoban.com/news/detail-838198.html
到了这里,关于数学建模-------误差来源以及误差分析的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!