贪心算法(区间问题)-Toy模板网

这篇具有很好参考价值的文章主要介绍了贪心算法(区间问题)。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

452. 用最少数量的箭引爆气球

题目(求无重复区间)

有一些球形气球贴在一堵用 XY 平面表示的墙面上。墙面上的气球记录在整数数组 points ，其中points[i] = [xstart, xend] 表示水平直径在 xstart 和 xend之间的气球。你不知道气球的确切 y 坐标。

一支弓箭可以沿着 x 轴从不同点 完全垂直 地射出。在坐标 x 处射出一支箭，若有一个气球的直径的开始和结束坐标为 x``start，x``end，且满足 xstart ≤ x ≤ x``end，则该气球会被引爆。可以射出的弓箭的数量 没有限制 。弓箭一旦被射出之后，可以无限地前进。

给你一个数组 points ，返回引爆所有气球所必须射出的最小弓箭数 。

示例 1：

输入：points = [[10,16],[2,8],[1,6],[7,12]]
输出：2
解释：气球可以用2支箭来爆破:
-在x = 6处射出箭，击破气球[2,8]和[1,6]。
-在x = 11处发射箭，击破气球[10,16]和[7,12]。

示例 2：

输入：points = [[1,2],[3,4],[5,6],[7,8]]
输出：4
解释：每个气球需要射出一支箭，总共需要4支箭。

示例 3：

输入：points = [[1,2],[2,3],[3,4],[4,5]]
输出：2
解释：气球可以用2支箭来爆破:
- 在x = 2处发射箭，击破气球[1,2]和[2,3]。
- 在x = 4处射出箭，击破气球[3,4]和[4,5]。

答案

class Solution {
    public int findMinArrowShots(int[][] points) {
        Arrays.sort(points,(a,b)->Integer.compare(a[0],b[0]));//不会溢出

        int res = 1;
        for(int i=1;i<points.length;i++){
            if(points[i][0]>points[i-1][1]){
                res++;
            }else{
                points[i][1] = Math.min(points[i-1][1],points[i][1]);
            }
        }
        return res;
    }
}

435. 无重叠区间

题目

给定一个区间的集合 intervals ，其中 intervals[i] = [starti, endi] 。返回 需要移除区间的最小数量，使剩余区间互不重叠 。

示例 1:

输入: intervals = [[1,2],[2,3],[3,4],[1,3]]
输出: 1
解释: 移除 [1,3] 后，剩下的区间没有重叠。

示例 2:

输入: intervals = [ [1,2], [1,2], [1,2] ]
输出: 2
解释: 你需要移除两个 [1,2] 来使剩下的区间没有重叠。

示例 3:

输入: intervals = [ [1,2], [2,3] ]
输出: 0
解释: 你不需要移除任何区间，因为它们已经是无重叠的了。

答案

class Solution {
    public int eraseOverlapIntervals(int[][] intervals) {
        Arrays.sort(intervals,(a,b)->Integer.compare(a[0],b[0]));

        int res = 1;
        for(int i=1;i<intervals.length;i++){
            if(intervals[i][0]>=intervals[i-1][1]){
                res++;
            }else{
                intervals[i][1] = Math.min(intervals[i-1][1],intervals[i][1]);
            }
        }
        return intervals.length - res;
    }
}

763. 划分字母区间

题目

给你一个字符串 s 。我们要把这个字符串划分为尽可能多的片段，同一字母最多出现在一个片段中。

注意，划分结果需要满足：将所有划分结果按顺序连接，得到的字符串仍然是 s 。

返回一个表示每个字符串片段的长度的列表。

示例 1：

输入：s = "ababcbacadefegdehijhklij"
输出：[9,7,8]
解释：
划分结果为 "ababcbaca"、"defegde"、"hijhklij" 。
每个字母最多出现在一个片段中。
像 "ababcbacadefegde", "hijhklij" 这样的划分是错误的，因为划分的片段数较少。

示例 2：

输入：s = "eccbbbbdec"
输出：[10]

答案

class Solution {
    public List<Integer> partitionLabels(String s) {
        int[] arr = new int[26];
        for(int i=0;i<s.length();i++){
            arr[s.charAt(i)-'a'] = i;
        }

        int pre = -1;
        int post = 0;
        List<Integer> list = new ArrayList(); 
        for(int i=0;i<s.length();i++){
            post = Math.max(post,arr[s.charAt(i)-'a']);
            if(i==post){
                list.add(post-pre);
                pre = post;
            }
        }
        return list;
    }
}

56. 合并区间

题目

以数组 intervals 表示若干个区间的集合，其中单个区间为 intervals[i] = [starti, endi] 。请你合并所有重叠的区间，并返回 一个不重叠的区间数组，该数组需恰好覆盖输入中的所有区间 。

示例 1：

输入：intervals = [[1,3],[2,6],[8,10],[15,18]]
输出：[[1,6],[8,10],[15,18]]
解释：区间 [1,3] 和 [2,6] 重叠, 将它们合并为 [1,6].

示例 2：

输入：intervals = [[1,4],[4,5]]
输出：[[1,5]]
解释：区间 [1,4] 和 [4,5] 可被视为重叠区间。

答案

class Solution {
    public int[][] merge(int[][] intervals) {
        Arrays.sort(intervals,(a,b)->Integer.compare(a[0],b[0]));

        List<int[]> list = new ArrayList();
        int start = intervals[0][0];
        int end = intervals[0][1];
        for(int i=1;i<intervals.length;i++){
            if(intervals[i][0]>end){
                list.add(new int[]{start,end});
                start = intervals[i][0];
                end = intervals[i][1];
            }else{ 
                end = Math.max(end,intervals[i][1]);
            }
        }
        list.add(new int[]{start,end});
        return list.toArray(new int[list.size()][]);
    }
}

738. 单调递增的数字

题目

当且仅当每个相邻位数上的数字 x 和 y 满足 x <= y 时，我们称这个整数是单调递增的。

给定一个整数 n ，返回小于或等于 n 的最大数字，且数字呈 单调递增 。

示例 1:

输入: n = 10
输出: 9

示例 2:

输入: n = 1234
输出: 1234

示例 3:

输入: n = 332
输出: 299

答案

class Solution {
    public int monotoneIncreasingDigits(int n) {
        String[] strs = (n+"").split("");

        int start = strs.length;
        for(int i=strs.length-1;i>0;i--){
            if(Integer.parseInt(strs[i-1])>Integer.parseInt(strs[i])){
                strs[i-1] = (Integer.parseInt(strs[i-1])-1)+"";
                start = i;
            }
        }
        for(int i=start;i<strs.length;i++){
            strs[i] = "9";
        }
        return Integer.parseInt(String.join("",strs));
    }
}

968. 监控二叉树

题目

给定一个二叉树，我们在树的节点上安装摄像头。

节点上的每个摄影头都可以监视其父对象、自身及其直接子对象。

计算监控树的所有节点所需的最小摄像头数量。

示例 1：

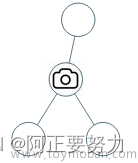
贪心算法(区间问题),算法题,贪心算法,算法

输入：[0,0,null,0,0]
输出：1
解释：如图所示，一台摄像头足以监控所有节点。

示例 2：

贪心算法(区间问题),算法题,贪心算法,算法文章来源地址https://www.toymoban.com/news/detail-838323.html

输入：[0,0,null,0,null,0,null,null,0]
输出：2
解释：需要至少两个摄像头来监视树的所有节点。 上图显示了摄像头放置的有效位置之一。

答案

class Solution {
    int res;
    public int minCameraCover(TreeNode root) {
        if(deal(root)==0){
            res++;
        }
        return res;
    }
    int deal(TreeNode root){//0 没有被监控  1 放监控  2 孩子监控  后序遍历
        if(root==null){
            return 2;
        }
        int left = deal(root.left);
        int right = deal(root.right);
        if(left==2 && right==2){
            return 0;
        }else if(left==0 || right==0){
            res++;
            return 1;
        }else{
            return 2;
        }
    }
}

到了这里，关于贪心算法(区间问题)的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！