学习笔记——动态规划(全)-Toy模板网

这篇具有很好参考价值的文章主要介绍了学习笔记——动态规划(全)。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

递推

1.递推和动态规划有什么关系？

递推问题包括动态规划，动态规划一定是递推，递推不一定是动态规划。
动态规划是一种决策性的问题，是在状态中做最优决策的一种特殊递推算法，通常的问法包括求最大最小值等，而递推可能还会包括求种类数等问题。

2.递推和递归的区别？

递推是一种算法，用来解决一类特殊的问题，而递归是程序实现的形式，不属于算法范畴。

3.递推问题求解的一般过程

1.状态定义（核心环节，f[i][j]:符号表达式以及对这个表达式的文字定义）
2.确定递推公式（形如dp [ i ][ j ]=dp [ i-1 ][ j ]+dp [ i ][ j-1 ]）
3.边界条件的确定（例如发dp [ 0 ][ 0 ]=0）
4.程序实现（包括递归加记忆化以及循环两种实现方式，后者通常更常用）

4.例题

1.兔子繁殖

题目描述
如果有一对小兔，每一个月都生下一对小兔，而所生下的每一对小兔在出生后的第三个月也都生下一对小兔。那么，由一对兔子开始，n 个月后有多少对小兔子呢？

输入
输入一个数字 n（1≤n≤100），代表题目中询问的月份。

输出
对于每个询问，输出一行整数，代表 n 月的时候，小兔子的数量。

样例输入1

4

样例输出1

5

样例输入2

65

样例输出2

27777890035288

状态定义： dp [ i ]代表第i天兔子的数量。
递推公式： dp [ i ]=f [ i-1 ]+f [ i-2 ]。
其中dp [ i-1 ]为第i天老兔子的数量，dp [ i-2 ]为第i天小兔子的数量。
边界条件： dp [ 1 ]=1,dp [ 2 ]=2。
程序实现：

#include<iostream>
#include<vector>
using namespace std;
#define MAXSIZE 100
//本题使用大整数版本来实现 
class BigInt:public vector<int>
{
	public:
		BigInt(){push_back(0);}
		BigInt(int x){
			push_back(x);
			proccess_digit();
		}
		BigInt &operator+=(const BigInt&a)
		{
			for(int i=0;i<a.size();i++)
			{
				if(i>=size())push_back(a[i]);
				else at(i)+=a[i];
			}
			proccess_digit();
			return*this;
		}
		BigInt operator+(const BigInt&a)
		{
			BigInt ret(*this);
			ret+=a;
			return ret;
		}
		void proccess_digit()
		{
			for(int i=0;i<size();i++)
			{
				if(at(i)<10)continue;
				if(i==size()-1)push_back(0);
				at(i+1)+=at(i)/10;
				at(i)%=10;
			}
			return ;
		}
};
BigInt dp[MAXSIZE+5];
ostream&operator<<(ostream &out,BigInt &a)
{
	for(int i=a.size()-1;i>=0;i--)
	out<<a[i];
	return out;
}
int main()
{
	int n;
	cin>>n;
	dp[1]=1;
	dp[2]=2;
	for(int i=3;i<=n;i++)
	dp[i]=dp[i-1]+dp[i-2];
	cout<<dp[n];
	return 0;
}

2.钱币问题

题目描述
某个国家的货币系统中，有 m 种面额的钱币，现在要用这 m 种面额的钱币凑足 n 元钱，问一共有多少种方法。m 种钱币不一定要都被用到。

例如，有 3 种钱币，分别为1、2、5，那么有四种方法拼凑出5元钱

(1，1，1，1，1) 全是1元钱
(1，2，2)，(1，1，1，2) 使用1元和2元
(5) 只用5元钱
注意：方案中的钱币不分顺序，也就是说（1，2，2）和（2，1，2）是同一种方法。

输入
输入两个数字 m, n（1≤m≤20,200≤n≤10000），第二行 m 个数字，代表 m 种钱币的面额，钱币面额大于0，数据中保证 m 种钱币各不相同。

输出
输出一个整数，代表拼凑出 n 元钱的方法数，答案有可能过大，请对 9973 取余。

样例输入1

8 200
1 2 5 10 20 50 100 200

样例输出1

3871

递推状态： dp[ i ][ j ]:选择前i种钱币，组成j元钱的方法总数。
递推公式： dp [ i ][ j ]=dp [ i-1 ][ j ]+dp [ i ][ j-money[ i ] ]。
dp [ i-1 ][ j ]为不使用第i种钱币的方法总数，dp [ i ][ j-money[ i ] ]为使用第i种钱币的方法总数，两者构成了 f [ i ][ j ]的全集。
边界条件： dp [ i ][ 0 ]=1,dp [ 0 ][ j ]=0。
代码实现：

#include<iostream>
using namespace std;
#define MAX_M 20
#define MAX_N 10000
int dp[MAX_M+5][MAX_N+5]={0};
int money[MAX_M+5];
int main()
{
	int m,n;
	cin>>m>>n;
	for(int i=1;i<=m;i++)
	cin>>money[i];
	for(int i=1;i<=m;i++)
	{
		dp[i][0]=1;
		for(int j=1;j<=n;j++)
		{
			dp[i][j]=dp[i-1][j];
			if(j<money[i])continue;
			dp[i][j]+=dp[i][j-money[i]];
			dp[i][j]%=9973;
		}
	}
	cout<<dp[m][n];
	return 0;
 }

3.爬楼梯

题目描述
小海是一个顽皮的少年，对于爬楼梯这种事情，他从来都不愿意一步一步走，每次上楼梯的时候，要么往上跨两级，要么往上跨三级。对于有 n 级台阶的楼梯，小海想知道他从最下面走到最上面的方法总数。

学习笔记——动态规划(全),学习,笔记,动态规划

输入
输入一个数字 n（1≤n≤500），代表台阶总数。

输出
输出一个整数，代表小海从最下面走到最上面的方法总数。

样例输入1

5

样例输出1

2

递推状态： dp[ i ]:走到第i层的方法总数。
递推公式： dp[ i ]=dp[ i-2 ]+dp[ i-3 ]。
走到第i层的方法总数为从i-2层走到i以及从i-3层走到i层的方法之和。
边界条件： dp[ 0 ]=1,dp[ 1 ]=0,dp[ 2 ]=1。
代码实现：

#include<iostream>
#include<vector>
using namespace std;
#define MAXSIZE 500
//本题使用大整数版本来实现 
class BigInt:public vector<int>
{
	public:
		BigInt(){push_back(0);}
		BigInt(int x){
			push_back(x);
			proccess_digit();
		}
		BigInt &operator+=(const BigInt&a)
		{
			for(int i=0;i<a.size();i++)
			{
				if(i>=size())push_back(a[i]);
				else at(i)+=a[i];
			}
			proccess_digit();
			return*this;
		}
		BigInt operator+(const BigInt&a)
		{
			BigInt ret(*this);
			ret+=a;
			return ret;
		}
		void proccess_digit()
		{
			for(int i=0;i<size();i++)
			{
				if(at(i)<10)continue;
				if(i==size()-1)push_back(0);
				at(i+1)+=at(i)/10;
				at(i)%=10;
			}
			return ;
		}
};
ostream&operator<<(ostream &out,BigInt &a)
{
	for(int i=a.size()-1;i>=0;i--)
	out<<a[i];
	return out;
}
BigInt dp[MAXSIZE+5];
int main()
{
	int n;
	cin>>n;
	dp[0]=1;dp[1]=0;dp[2]=1;
	for(int i=3;i<=n;i++)
	dp[i]=dp[i-2]+dp[i-3];
	cout<<dp[n];
	return 0;
}

4.墙壁涂色

题目描述
给一个环形的墙壁涂颜色，颜色一共有 k 种，墙壁被竖直地划分成 n 个部分，相邻的部分颜色不能相同。请你写程序计算出一共有多少种给墙壁上色的方案？

例如，当 n=5,k=3 时，下面是一种合法的涂色方案

学习笔记——动态规划(全),学习,笔记,动态规划

而由于墙壁是环形的，所以下面就是一种非法的方案

学习笔记——动态规划(全),学习,笔记,动态规划

输入
输入两个数字 n，k（1≤n≤103，2≤k≤10），分别代表墙壁数量和颜色种类。

输出
对于每个询问，输出一行整数，合法的墙壁涂色方案数。

样例输入1

5 3

样例输出1

30

递推状态： dp[ n ][ i ][ j ]:以i开头，以j结尾长度为n的情况总数。（非最优定义）
递推公式： dp[ n ][ i ][ j ]=sum(dp[ n-1 ][ i ][ k ])(k!=j)
以i开头，以j结尾长度为n的情况总数,为长度为n-1，且最后一位不为j的情况之和。
边界条件： dp[ 1 ][ i ][ i ]=1,dp[ 2 ][ i ][ j ]=1(i!=j)。
代码实现：

#include<iostream>
#include<vector>
using namespace std;
#define MAX_N 1000
#define MAX_K 10
//本题使用大整数版本来实现 
class BigInt:public vector<int>
{
	public:
		BigInt(){push_back(0);}
		BigInt(int x){
			push_back(x);
			proccess_digit();
		}
		BigInt &operator+=(const BigInt&a)
		{
			for(int i=0;i<a.size();i++)
			{
				if(i>=size())push_back(a[i]);
				else at(i)+=a[i];
			}
			proccess_digit();
			return*this;
		}
		BigInt operator+(const BigInt&a)
		{
			BigInt ret(*this);
			ret+=a;
			return ret;
		}
		void proccess_digit()
		{
			for(int i=0;i<size();i++)
			{
				if(at(i)<100000)continue;
				if(i==size()-1)push_back(0);
				at(i+1)+=at(i)/100000;
				at(i)%=100000;
			}
			return ;
		}
};
ostream&operator<<(ostream &out,BigInt &a)
{
	out<<a[a.size()-1]; 
	for(int i=a.size()-2;i>=0;i--)
	{
		for(int j=10000;j>0;j/=10)
		{
			out<<a[i]%(j*10)/j;
		}
	}
	return out;
}
BigInt dp[2][MAX_K+5][MAX_K+5]={0};//滚动数组避免内存超限 
int main()
{
	int n,k;
	cin>>n>>k;
	for(int i=1;i<=k;i++)dp[1][i][i]=1;
	for(int i=1;i<=k;i++)
	{
		for(int j=1;j<=k;j++)
		{
			if(i!=j)dp[0][i][j]=1;
		}
	}
	for(int s=3;s<=n;s++)
	{
		for(int i=1;i<=k;i++)
		{
			for(int j=1;j<=k;j++)
			{
				dp[s%2][i][j]=0;
				for(int l=1;l<=k;l++)
				{	
					if(l==j)continue;
					dp[s%2][i][j]+=dp[(s-1)%2][i][l];
				}
			}
		}
	}
	BigInt ans=0;
	for(int i=1;i<=k;i++)
	{
		for(int j=1;j<=k;j++)
		{
			if(i==j)continue;
			ans+=dp[n%2][i][j]; 
		}
	}
	cout<<ans;
	return 0;
}

5.数的划分

题目描述

将整数 $n$ 分成 $k$ 份，且每份不能为空，任意两个方案不相同（不考虑顺序）。

例如： $n = 7$ ， $k = 3$ ，下面三种分法被认为是相同的。

$1, 1, 5$ ;
$1, 5, 1$ ;
$5, 1, 1$ .

问有多少种不同的分法。

输入格式

$n, k$ （ $\le 200$ ， $\le k \le 6$ ）

输出格式

$1$ 个整数，即不同的分法。

样例 #1

样例输入 #1

7 3

样例输出 #1

提示

四种分法为：
$1, 1, 5$ ;
$1, 2, 4$ ;
$1, 3, 3$ ;
$2, 2, 3$ .

递推状态： dp[ i ][ j ]：整数i被分成j份的方法总数。
递推公式： dp[ i ][ j ]=dp[ i-1 ][ j-1 ]+dp[ i-j ][ j ]。
整数i被分成j份的方法总数包含含有1的方法总数与不含有1的方法总数。
边界条件： dp[ i ][ 1 ]=1,dp[ 0 ][ 0 ]=1.。
代码实现：

#include<iostream>
using namespace std;
#define MAX_N 200
#define MAX_K 6
int dp[MAX_N+5][MAX_K+5]={0};
int main()
{
	int n,k;
	cin>>n>>k;
	dp[0][0]=1;
	for(int i=1;i<=n;i++)
	{
		dp[i][1]=1;
		for(int j=2;j<=min(i,k);j++)
		{
			dp[i][j]=dp[i-1][j-1]+dp[i-j][j];
		}
	}
	cout<<dp[n][k];
	return 0;
 }

6.数的计算

题目描述

给出正整数 $n$ ，要求按如下方式构造数列：

只有一个数字 $n$ 的数列是一个合法的数列。
在一个合法的数列的末尾加入一个正整数，但是这个正整数不能超过该数列最后一项的一半，可以得到一个新的合法数列。

请你求出，一共有多少个合法的数列。两个合法数列 $a, b$ 不同当且仅当两数列长度不同或存在一个正整数 $\leq |a|$ ，使得 $a_i \neq b_i$ 。

输入格式

输入只有一行一个整数，表示 $n$ 。

输出格式

输出一行一个整数，表示合法的数列个数。

样例 #1

样例输入 #1

样例输出 #1

提示

样例 1 解释

满足条件的数列为：

$6$
$6, 1$
$6, 2$
$6, 3$
$6, 2, 1$
$6, 3, 1$

数据规模与约定

对于全部的测试点，保证 $\leq n \leq 10^3$ 。

递推状态： dp[ i ]:以i开始的数的合法序列数。
递推公式： dp[ i ]=sum(dp[ j ])+1 (i/2>=j>=1)
dp[ i ]包括以i结尾的序列数1与以j开头的序列数的和。
代码实现：

#include<iostream>
using namespace std;
#define MAXSIZE 1000
int dp[MAXSIZE+5];
int main()
{
	int n;
	cin>>n;
	for(int i=1;i<=n;i++)
	{
		dp[i]=1;
		for(int j=1;j<=i/2;j++)	
		dp[i]+=dp[j];
	}
	cout<<dp[n];
	return 0;
}

7.神经网络

题目背景

人工神经网络（Artificial Neural Network）是一种新兴的具有自我学习能力的计算系统，在模式识别、函数逼近及贷款风险评估等诸多领域有广泛的应用。对神经网络的研究一直是当今的热门方向，兰兰同学在自学了一本神经网络的入门书籍后，提出了一个简化模型，他希望你能帮助他用程序检验这个神经网络模型的实用性。

题目描述

在兰兰的模型中，神经网络就是一张有向图，图中的节点称为神经元，而且两个神经元之间至多有一条边相连，下图是一个神经元的例子：

学习笔记——动态规划(全),学习,笔记,动态规划

神经元（编号为 $i$ ）

图中， $X_1 \sim X_3$ 是信息输入渠道， $Y_1 \sim Y_2$ 是信息输出渠道， $C_i$ 表示神经元目前的状态， $U_i$ 是阈值，可视为神经元的一个内在参数。

神经元按一定的顺序排列，构成整个神经网络。在兰兰的模型之中，神经网络中的神经元分为几层；称为输入层、输出层，和若干个中间层。每层神经元只向下一层的神经元输出信息，只从上一层神经元接受信息。下图是一个简单的三层神经网络的例子。

学习笔记——动态规划(全),学习,笔记,动态规划

兰兰规定， $C_i$ 服从公式：（其中 $n$ 是网络中所有神经元的数目）

$C_i=\left(\sum\limits_{(j,i) \in E} W_{ji}C_{j}\right)-U_{i}$

公式中的 $W_{ji}$ （可能为负值）表示连接 $j$ 号神经元和 $i$ 号神经元的边的权值。当 $C_i$ 大于 $0$ 时，该神经元处于兴奋状态，否则就处于平静状态。当神经元处于兴奋状态时，下一秒它会向其他神经元传送信号，信号的强度为 $C_i$ 。

如此．在输入层神经元被激发之后，整个网络系统就在信息传输的推动下进行运作。现在，给定一个神经网络，及当前输入层神经元的状态（ $C_i$ ），要求你的程序运算出最后网络输出层的状态。

输入格式

输入文件第一行是两个整数 $n$ （ $\le n \le 100$ ）和 $p$ 。接下来 $n$ 行，每行 $2$ 个整数，第 $i + 1$ 行是神经元 $i$ 最初状态和其阈值（ $U_i$ ），非输入层的神经元开始时状态必然为 $0$ 。再下面 $p$ 行，每行有两个整数 $i, j$ 及一个整数 $W_{ij}$ ，表示连接神经元 $i, j$ 的边权值为 $W_{ij}$ 。

输出格式

输出文件包含若干行，每行有 $2$ 个整数，分别对应一个神经元的编号，及其最后的状态， $2$ 个整数间以空格分隔。仅输出最后状态大于 $0$ 的输出层神经元状态，并且按照编号由小到大顺序输出。

若输出层的神经元最后状态均小于等于 $0$ ，则输出 NULL。

样例 #1

样例输入 #1

样例输出 #1

3 1
4 1
5 1

代码实现

#include<iostream>
#include<vector>
#include<queue>
using namespace std;
#define MAX_N 100
int w[MAX_N+5][MAX_N+5]={0};
int u[MAX_N+5],c[MAX_N+5];
int indeg[MAX_N+5]={0},outdeg[MAX_N+5]={0};
vector<int>after[MAX_N+5]; 
int main()
{
	int n,p;
	cin>>n>>p;
	for(int i=1;i<=n;i++)
	cin>>c[i]>>u[i];
	for(int i=1,a,b,W;i<=p;i++)
	{
		cin>>a>>b>>W;
		indeg[b]+=1;
		outdeg[a]+=1;
		w[a][b]=W;
		after[a].push_back(b);
	}
	for(int i=1;i<=n;i++)
	if(indeg[i]!=0)c[i]-=u[i];
	queue<int>q;
	for(int i=1;i<=n;i++)
	if(indeg[i]==0)q.push(i);
	while(!q.empty())//拓扑序 
	{
		int fro=q.front();
		q.pop();
		for(int i=0;i<after[fro].size();i++)
		{
			int to=after[fro][i];
			if(c[fro]>0)c[to]+=c[fro]*w[fro][to];
			indeg[to]--;
			if(indeg[to]==0)q.push(to);
		}
	}
	int flag=1;
	for(int i=1;i<=n;i++)
	{
		if(outdeg[i])continue;
		if(c[i]<=0)continue;
		cout<<i<<" "<<c[i]<<endl;
		flag=0;
	}
	if(flag)cout<<"NULL"<<endl;
	return 0;
}

8.栈

题目背景

栈是计算机中经典的数据结构，简单的说，栈就是限制在一端进行插入删除操作的线性表。

栈有两种最重要的操作，即 pop（从栈顶弹出一个元素）和 push（将一个元素进栈）。

栈的重要性不言自明，任何一门数据结构的课程都会介绍栈。宁宁同学在复习栈的基本概念时，想到了一个书上没有讲过的问题，而他自己无法给出答案，所以需要你的帮忙。

题目描述

学习笔记——动态规划(全),学习,笔记,动态规划

宁宁考虑的是这样一个问题：一个操作数序列， $1,2,\ldots ,n$ （图示为 1 到 3 的情况），栈 A 的深度大于 $n$ 。

现在可以进行两种操作，

将一个数，从操作数序列的头端移到栈的头端（对应数据结构栈的 push 操作）
将一个数，从栈的头端移到输出序列的尾端（对应数据结构栈的 pop 操作）

使用这两种操作，由一个操作数序列就可以得到一系列的输出序列，下图所示为由 1 2 3 生成序列 2 3 1 的过程。

学习笔记——动态规划(全),学习,笔记,动态规划

（原始状态如上图所示）

你的程序将对给定的 $n$ ，计算并输出由操作数序列 $1,2,\ldots,n$ 经过操作可能得到的输出序列的总数。

输入格式

输入文件只含一个整数 $n$ （ $\leq n \leq 18$ ）。

输出格式

输出文件只有一行，即可能输出序列的总数目。

样例 #1

样例输入 #1

样例输出 #1

递推状态： dp[ i ]：i个数的出栈序列数。
递推公式： dp[ i ]=sum(dp[ j-1 ]*dp[ n-j ]) (1<=j<=i)
前i个数的出栈序列数为以第j个数为最后一个出栈元素的序列总和。
边界条件： dp[ 0 ]=1
代码实现：

#include<iostream>
using namespace std;
#define MAX_N 18
int dp[MAX_N+5]={0};
int main()
{
	int n;
	cin>>n;
	dp[0]=1;
	for(int i=1;i<=n;i++)
	{
		for(int j=1;j<=i;j++)
		{
			int x=dp[j-1]*dp[i-j];
			dp[i]+=x;
		}
	}
	cout<<dp[n];
	return 0;
 }

9.循环

题目描述

乐乐是一个聪明而又勤奋好学的孩子。他总喜欢探求事物的规律。一天，他突然对数的正整数次幂产生了兴趣。

众所周知， $2$ 的正整数次幂最后一位数总是不断的在重复 $2, 4, 8, 6, 2, 4, 8, 6 \dots$ 我们说 $2$ 的正整数次幂最后一位的循环长度是 $4$ （实际上 $4$ 的倍数都可以说是循环长度，但我们只考虑最小的循环长度）。类似的，其余的数字的正整数次幂最后一位数也有类似的循环现象：

$\def\arraystretch{1.5} \begin{array}{c|c|c}\hline \textbf{数字}& \textbf{循环} & \textbf{循环长度} \cr\hline\hline 2 & 2,4,8,6 & 4\cr\hline 3 & 3,9,7,1 & 4\cr\hline 4 & 4,6 & 2\cr\hline 5 & 5 & 1\cr\hline 6 & 6 & 1\cr\hline 7 & 7,9,3,1 & 4\cr\hline 8 & 8,4,2,6 & 4\cr\hline 9 & 9,1 & 2\cr\hline \end{array}$

这时乐乐的问题就出来了：是不是只有最后一位才有这样的循环呢？对于一个整数 $n$ 的正整数次幂来说，它的后 $k$ 位是否会发生循环？如果循环的话，循环长度是多少呢？

注意：

如果 $n$ 的某个正整数次幂的位数不足 $k$ ，那么不足的高位看做是 $0$ 。
如果循环长度是 $L$ ，那么说明对于任意的正整数 $a$ ， $n$ 的 $a$ 次幂和 $a + L$ 次幂的最后 $k$ 位都相同。

输入格式

共一行，包含两个整数 $n$ 和 $k$ 。 $n$ 和 $k$ 之间用一个空格隔开，表示要求 $n$ 的正整数次幂的最后 $k$ 位的循环长度。

输出格式

一个整数，表示循环长度。如果循环不存在，输出 $- 1$ 。
样例 #1

样例输入 #1

32 2

样例输出 #1

提示

【数据范围】

对于 $\%$ 的数据，满足 $\le 4$ ；
对于 $\%$ 的数据，满足 $\le n < {10}^{100}$ ， $\le k \le 100$ 。

代码实现

#include <iostream>
#include <vector>
using namespace std;

class BigInt : public vector<int> {
public :
    BigInt() { push_back(0); }
    BigInt(int n, int v) : vector<int>(n, v) {}
    BigInt(int x) {
        push_back(x);
        proccess_digit();
        return ;
    }
    BigInt(string &s, int k) {
        for (int i = 0, j = s.size() - 1; i < k; i++, j--) {
            push_back(s[j] - '0');
        }
        return ;
    }
    BigInt &operator *=(int x) {
        for (int i = 0; i < size(); i++) at(i) *= x;
        proccess_digit();
        return *this;
    }
    BigInt operator*(const BigInt &a) {
        BigInt ret(min(MaxLen, int(size() + a.size() - 1)), 0);
        for (int i = 0; i < size(); i++) {
            for (int j = 0; j < a.size(); j++) {
                if (i + j >= MaxLen) continue;
                ret[i + j] += at(i) * a[j];
            }
        }
        ret.proccess_digit();
        return ret;
    }

    static int MaxLen;

private:
    void proccess_digit() {
        for (int i = 0; i < size(); i++) {
            if (at(i) < 10) continue;
            if (i + 1 < MaxLen) {
                if (i + 1 == size()) push_back(0);
                at(i + 1) += at(i) / 10;
            }
            at(i) %= 10;
        }
        return ;
    }
};

int BigInt::MaxLen = 0;

ostream &operator<<(ostream &out, const BigInt &a) {
    for (int i = a.size() - 1; i >= 0; --i) {
        out << a[i];
    }
    return out;
}

int main() {
    string s;
    int k;
    cin >> s >> k;
    BigInt::MaxLen = k;
    BigInt n(s, k);
    BigInt pre_y = n, y;
    vector<int> arr;
    for (int i = 0; i < n.size(); i++) {
        y = pre_y;
        int cnt = 1;
        while ((y * n).at(i) != n[i]) {
            y = y * pre_y;
            cnt += 1;
            if (cnt == 11) break;
        }
        if (cnt == 11) {
            cout << "-1" << endl;
            return 0;
        }
        arr.push_back(cnt);
        pre_y = y;
    }
    BigInt ans = 1;
    for (int i = 0; i < arr.size(); i++) {
        ans *= arr[i];
    }
    cout << ans << endl;
    return 0;
}

10.传球游戏

题目描述

上体育课的时候，小蛮的老师经常带着同学们一起做游戏。这次，老师带着同学们一起做传球游戏。

游戏规则是这样的： $n$ 个同学站成一个圆圈，其中的一个同学手里拿着一个球，当老师吹哨子时开始传球，每个同学可以把球传给自己左右的两个同学中的一个（左右任意），当老师再次吹哨子时，传球停止，此时，拿着球没有传出去的那个同学就是败者，要给大家表演一个节目。

聪明的小蛮提出一个有趣的问题：有多少种不同的传球方法可以使得从小蛮手里开始传的球，传了 $m$ 次以后，又回到小蛮手里。两种传球方法被视作不同的方法，当且仅当这两种方法中，接到球的同学按接球顺序组成的序列是不同的。比如有三个同学 $1$ 号、 $2$ 号、 $3$ 号，并假设小蛮为 $1$ 号，球传了 $3$ 次回到小蛮手里的方式有 $\rightarrow 2 \rightarrow 3 \rightarrow 1$ 和 $\rightarrow 3 \rightarrow 2 \rightarrow 1$ ，共 $2$ 种。

输入格式

一行，有两个用空格隔开的整数 $\le n \le 30,1 \le m \le 30)$ 。

输出格式

$1$ 个整数，表示符合题意的方法数。

样例 #1

样例输入 #1

3 3

样例输出 #1

提示

数据范围及约定

对于 $40\%$ 的数据，满足： $\le n \le 30,1 \le m \le 20$ ；
对于 $100\%$ 的数据，满足： $\le n \le 30,1 \le m \le 30$ 。

递推状态： dp[ i ][ j ]:第i次到达j的方法总数。
递推公式：
dp[ i ][ j ]=dp[ i-1 ][ j-1 ]+dp[ i-1 ][ j+1] (1<j<n)
dp[ i ][ 1 ]=dp[ i-1 ][ 2 ]+dp[ i-1 ][ n ]
dp[ i ][ n ]=dp[ i-1 ][ 1 ]+dp[ i-1 ][ n-1 ]
边界条件： dp[ 0 ][ 1 ]=1
代码实现：

#include<iostream>
using namespace std;
#define MAXSIZE 30
int dp[MAXSIZE+5][MAXSIZE+5]={0};
int main()
{
	int n,m;
	cin>>n>>m;
	dp[0][1]=1;
	for(int i=1;i<=m;i++)
	{
		for(int j=2;j<n;j++)
		{
			dp[i][j]=dp[i-1][j+1]+dp[i-1][j-1];
		}
		dp[i][1]=dp[i-1][2]+dp[i-1][n];
		dp[i][n]=dp[i-1][1]+dp[i-1][n-1];
	}
	cout<<dp[m][1];
	return 0;
}

11.Honoi双塔问题

题目描述

给定 A、B、C 三根足够长的细柱，在 A 柱上放有 $2 n$ 个中间有孔的圆盘，共有 $n$ 个不同的尺寸，每个尺寸都有两个相同的圆盘，注意这两个圆盘是不加区分的（下图为 $n = 3$ 的情形）。

学习笔记——动态规划(全),学习,笔记,动态规划

现要将这些圆盘移到 C 柱上，在移动过程中可放在 B 柱上暂存。要求：

每次只能移动一个圆盘；
A、B、C 三根细柱上的圆盘都要保持上小下大的顺序。

任务：设 $A_n$ 为 $2 n$ 个圆盘完成上述任务所需的最少移动次数，对于输入的 $n$ ，输出 $A_n$ 。

输入格式

一个正整数 $n$ ，表示在 A 柱上放有 $2 n$ 个圆盘。

输出格式

一个正整数, 为完成上述任务所需的最少移动次数 $A_n$ 。

样例 #1

样例输入 #1

样例输出 #1

样例 #2

样例输入 #2

样例输出 #2

提示

限制

对于 $50\%$ 的数据， $\le n \le 25$ ；
对于 $100\%$ 的数据， $\le n \le 200$ 。

提示

设法建立 $A_n$ 与 $A_{n-1}$ 的递推关系式。

递推状态： dp[ i ]：n=i时的交换总次数。
递推公式： dp[ i ]=dp[ i-1 ]*2+2。
将2i个圆盘转移到C的次数为将2(i-1)个圆盘转移到B，将2个圆盘转移到C，再把2(i-1)个圆盘转移到C的次数和。
边界条件： dp[ 1 ]=2。
代码实现：

#include<iostream>
#include<vector>
using namespace std;
#define MAX_N 200
class BigInt:public vector<int>{
	public:
		BigInt(){push_back(0);}
		BigInt(int x)
		{
			push_back(x);
			proccess_digit();
		}
		BigInt operator+=(int x)
		{
			at(0)+=x;
			proccess_digit();
			return *this;
		}
		BigInt operator+(int x)
		{
			BigInt ret(*this);
			ret+=x;
			return ret;
		}
		BigInt operator*=(int x)
		{
			for(int i=0;i<size();i++)
			{	
				at(i)*=x;
			}
			proccess_digit();
			return *this;
		}
		BigInt operator*(int x)
		{
			BigInt ret(*this);
			ret*=x;
			return ret;
		}
		void proccess_digit()
		{
			for(int i=0;i<size();i++)
			{
				if(at(i)<10)continue;
				if(i==size()-1)push_back(0);
				at(i+1)+=at(i)/10;
				at(i)%=10;
			}
			return ;
		}
};
ostream &operator<<(ostream &out, const BigInt &a) {
    for (int i = a.size() - 1; i >= 0; i--) {
        out << a[i];
    }
    return out;
}
BigInt dp[MAX_N+5];
int main()
{
	int n;
	cin>>n;
	dp[1]=2;
	for(int i=2;i<=n;i++)
	{
		dp[i]=dp[i-1]*2+2;
	}
	cout<<dp[n];
	return 0;
}

动态规划

1.动态规划求解的一般过程

1、确定动归状态
例如：f(i,j) 代表从底边走到 (i,j) 点所能获得的最大值

2、确定状态转移方程
学习笔记——动态规划(全),学习,笔记,动态规划

3、正确性证明：求助于数学归纳法

4、程序实现（递归+记忆化或循环）

2.重要概念

学习笔记——动态规划(全),学习,笔记,动态规划

3.例题

1.数字三角形

题目描述
有一个由数字组成的三角形数塔，站在上一层的某个点，只能到达其下方左右的两个点。现在请找到一条从上到下的路径，使得路径上所有数字相加之和最大

学习笔记——动态规划(全),学习,笔记,动态规划

输入
第一行输入一个数字 n（1≤n≤1000）代表数塔层数

接下来n行，按数塔图形，每行有一个或多个的整数，表示该层节点的值（节点值≤100000）
输出
输出一个整数，代表从上到下路径上所有数字相加和的最大值。

本题 BUG 已解决！

样例输入1

6
3
9 5
4 2 1
3 4 9 6
3 5 3 7 3
2 1 3 9 3 2

样例输出1

39

动归状态 dp[ i ][ j ]：从最底层到达第i行第j个位置的最大值
动归方程 dp[ i ][ j ]=max(dp[ i+1 ][ j ]+dp[ i+1 ][ j+1 ])+val[ i ]
代码实现

#include<iostream>
using namespace std;
#define MAXSIZE 1000
int dp[MAXSIZE+5][MAXSIZE+5]={0};
int main()
{
	int n;
	cin>>n;
	for(int i=1;i<=n;i++)
	{
		for(int j=1;j<=i;j++)
		{
			cin>>dp[i][j];
		}
	}
	for(int i=n;i>=1;i--)
	{
		for(int j=1;j<=i;j++)
		{
			dp[i][j]+=max(dp[i+1][j],dp[i+1][j+1]);	
		}
	}
	cout<<dp[1][1];
	return 0;
}

学习笔记——动态规划(全),学习,笔记,动态规划

2.0/1背包

题目描述
给一个能承重V的背包，和n件物品，我们用重量和价值的二元组来表示一个物品，第i件物品表示为（Vi，Wi），问：在背包不超重的情况下，得到物品的最大价值是多少？
学习笔记——动态规划(全),学习,笔记,动态规划

输入
第一行输入两个数 V,n，分别代表背包的最大承重和物品数。

接下来n行，每行两个数Vi,Wi，分别代表第i件物品的重量和价值。

(Vi≤V≤10000,n≤100,Wi≤1000000)
输出
输出一个整数，代表在背包不超重情况下所装物品的最大价值。

样例输入1

15 4
4 10
3 7
12 12
9 8

样例输出1

19

动归状态 dp[ i ][ j ]：前i件物品在背包承重为j的情况下的最大价值。
动归方程 dp[ i ][ j ]=max(dp[ i-1 ][ j-v[ i ] ]+w[ i ],dp[ i-1 ][ j ])。
代码实现1（基础版本）

#include<iostream>
using namespace std;
#define MAX_V 10000
#define MAX_N 100
int dp[MAX_N+5][MAX_V+5]={0};
int main()
{
	int V,n;
	cin>>V>>n;
	for(int i=1,vi,wi;i<=n;i++)
	{
		cin>>vi>>wi;
		for(int j=1;j<=V;j++)
		{
			dp[i][j]=dp[i-1][j];
			if(j>=vi)dp[i][j]=max(dp[i][j],dp[i-1][j-vi]+wi);
		}
	}
	cout<<dp[n][V];
	return 0;
 }

代码实现2（滚动数组）

#include<iostream>
using namespace std;
#define MAX_V 10000
#define MAX_N 100
int dp[2][MAX_V+5]={0};
int main()
{
	int V,n;
	cin>>V>>n;
	for(int i=1,vi,wi;i<=n;i++)
	{
		cin>>vi>>wi;
		for(int j=1;j<=V;j++) 
		{
			dp[i%2][j]=dp[1-i%2][j];
			if(j>=vi)dp[i%2][j]=max(dp[i%2][j],dp[1-i%2][j-vi]+wi);
		}
	}
	cout<<dp[n%2][V];
	return 0;
 }

代码实现3（一维数组）

#include<iostream>
using namespace std;
#define MAX_V 10000
#define MAX_N 100
int dp[MAX_V+5]={0};
int main()
{
	int V,n;
	cin>>V>>n;
	for(int i=1,vi,wi;i<=n;i++)
	{
		cin>>vi>>wi;
		for(int j=V;j>=vi;j--)//注意这里要从后向前 
		{
			dp[j]=max(dp[j],dp[j-vi]+wi);
		}
	}
	cout<<dp[V];
	return 0;
 }

3.完全背包

题目描述
有N种物品和一个容量为 V 的背包，每种物品都有无限件可用。

第 i 种物品的体积是Ci，价值是Wi。求解在不超过背包容量的情况下，能够获得的最大价值。

学习笔记——动态规划(全),学习,笔记,动态规划

输入
第一行为两个整数N、V(1≤N,V≤10000)，分别代表题目描述中的物品种类数量N和背包容量V。

后跟N行，第 i 行两个整数Ci、Vi，分别代表每种物品的体积和价值。

输出
输出一个整数，代表可获得的最大价值。

样例输入

5 20
2 3
3 4
10 9
5 2
11 11

样例输出

30

动归状态 dp[ i ][ j ]：前i种物品在背包承重为j的情况下的最大价值。
动归方程 dp[ i ][ j ]=max(dp[ i ][ j-v[ i ] ]+w[ i ],dp[ i-1 ][ j ])。
代码实现

#include<iostream>
using namespace std;
#define MAXSIZE 10000
int dp[MAXSIZE+5]={0};
int main()
{
	int N,V;
	cin>>N>>V;
	for(int i=1,ci,wi;i<=N;i++)
	{
		cin>>ci>>wi;
		for(int j=ci;j<=V;j++)//注意此时正向刷表，和0/1背包区分 
		{
			dp[j]=max(dp[j],dp[j-ci]+wi);
		}
	}
	cout<<dp[V];
	return 0;
}

4.多重背包

题目描述
给有一个能承重 V 的背包，和n种物品，每种物品的数量有限多，我们用重量、价值和数量的三元组来表示一个物品，第 i 件物品表示为（Vi，Wi，Si），问在背包不超重的情况下，得到物品的最大价值是多少？

学习笔记——动态规划(全),学习,笔记,动态规划

输入
第一行输入两个数V、n，分别代表背包的最大承重和物品种类数。

接下来 n 行，每行三个数 Vi、Wi、Si，分别代表第 i 种物品的重量、价值和数量。

输出
输出一个整数，代表在背包不超重情况下所装物品的最大价值。

样例输入1

15 4
4 10 5
3 7 4
12 12 2
9 8 7

样例输出1

37

思路： 把该问题转化为0/1背包问题去做。（不是最优，后面会有优化）

#include<iostream>
using namespace std;
#define MAX_V 100000
#define MAX_S 100000
#define MAX_N 100
int dp[MAX_V+5]={0};
int main()
{
	int V,N;
	cin>>V>>N;
	for(int i=1,vi,wi,si;i<=N;i++)
	{
		cin>>vi>>wi>>si;
		for(int j=1;j<=si;j++)
		{
			for(int k=V;k>=vi;k--)
			{
				dp[k]=max(dp[k],dp[k-vi]+wi);
			}
		}
	}
	cout<<dp[V];
	return 0;
}

5.最长上升子序列

题目描述
有一个数字序列，求其中最长严格上升子序列的长度

学习笔记——动态规划(全),学习,笔记,动态规划

输入
输入一个数字n (1≤n≤1000000)，代表数字序列的长度。

后跟 n 个整数，第 i 个整数 ai(1≤ai≤10000)，代表数字序列中的第 i 个值。

输出
输出一个整数，代表所求的最长严格上升子序列的长度。

样例输入

10
3 2 5 7 4 5 7 9 6 8

样例输出

5

动归状态 dp[ i ]：以i结尾的上升子序列的最大长度。
动归方程 dp[ i ]=max(dp[ j ]+1)(0<j<i且arr[ j ]<arr[ i ])。
代码实现（非最优实现）

#include<iostream>
using namespace std;
#define MAX_N 1000000
int dp[MAX_N]={0};
int arr[MAX_N];
int main()
{
	int n;
	cin>>n;
	for(int i=1;i<=n;i++)
	{
		scanf("%d",&arr[i]);
	}
	int ans=0;
	for(int i=1;i<=n;i++)
	{
		dp[i]=1;
		for(int j=0;j<i;j++)
		{
			if(arr[j]<arr[i])dp[i]=max(dp[i],dp[j]+1);
		}
		ans=max(ans,dp[i]);
	}
	cout<<ans;
	return 0;
 }

6.最长公共子序列

题目描述
给出两个字符串，求其两个的最长公共子序列长度。

输入
第一行输入一个字符串s1，第二行输入一个字符串s2 (字符串长度≤1000) ，两个字符串长度可以不相同。

输出
输出一个整数，代表两个字符串的最长公共子序列的长度。

样例输入1

sehuaizexi
yhaizeyiux

样例输出1

6

动归状态 dp[ i ][ j ]：s1的前i位和s2的前j位的最长公共子序列。
动归方程 dp[ i ]=max(dp[ i-1 ][ j ],dp[ i ][ j-1 ]) (s1[ i ]!=s2[ j ])
dp[ i ][ j ]=dp[ i-1 ][ j-1 ]+1(s1[ i ]=s2[ j ])
代码实现

#include<iostream>
#include<cstring>
using namespace std;
#define MAX_N 1000
int dp[MAX_N+5][MAX_N+5]={0};
char s1[MAX_N+5],s2[MAX_N+5];
int main()
{
	cin>>(s1+1);
	cin>>(s2+1);
	int len1=strlen(s1+1),len2=strlen(s2+1);
	for(int i=1;i<=len1;i++)
	{
		for(int j=1;j<=len2;j++)
		{
		if(s1[i]==s2[j])dp[i][j]=dp[i-1][j-1]+1;
		else dp[i][j]=max(dp[i-1][j],dp[i][j-1]);
		}
	}
	cout<<dp[len1][len2];
	return 0;
}

7.切割回文

题目描述
给出一个字符串S，问对字符串S最少切几刀，使得分成的每一部分都是一个回文串（注意：单一字符是回文串）

学习笔记——动态规划(全),学习,笔记,动态规划

输入
一个长度为n(1≤n≤500000)的字符串S，只包含小写字母。

输出
输出一个整数，代表所切的最少刀数。

样例输入

sehuhzzexe

样例输出

4

动归状态 dp[ i ][ j ]：在区间[i,j]内的最少切割次数。
动归方程
学习笔记——动态规划(全),学习,笔记,动态规划
本题为
代码实现（非最优实现，区间dp）

#include<iostream>
#include<cstring>
#include<cinttypes>
using namespace std;
#define MAX_N 5000
int dp[MAX_N+5][MAX_N+5];
char arr[MAX_N+5];
int main()
{
	scanf("%s",arr+1);
	int n=strlen(arr+1);
	for(int l=1;l<=n;l++)
	{
		for(int i=1;i<=n-l+1;i++)
		{
			int j=i+l-1;
			if(arr[i]==arr[j]&&dp[i+1][j-1]==0)dp[i][j]=0;
			else
			{
				dp[i][j]=l;
				for(int k=i;k<j;k++)
				{
					dp[i][j]=min(dp[i][j],dp[i][k]+dp[k+1][j]+1);
				}
			}
		}		
	}
	cout<<dp[1][n];
	return 0;
 }

8.棋盘分割

题目描述
将一个８*８的棋盘进行如下分割：将原棋盘割下一块矩形棋盘并使剩下部分也是矩形，再将剩下的部分继续如此分割，这样割了(n−1)次后，连同最后剩下的矩形棋盘共有 n 块矩形棋盘。(每次切割都只能沿着棋盘格子的边进行)

学习笔记——动态规划(全),学习,笔记,动态规划

原棋盘上每一格有一个分值，一块矩形棋盘的总分为其所含各格分值之和。现在需要把棋盘按上述规则分割n块矩形棋盘，并使各矩形棋盘总分的平方和最小。

请编程对给出的棋盘及 n，求出平方和的最小值。

输入
第1行为一个整数n(1<n<15)。

第2行至第9行每行为8个小于100的非负整数，表示棋盘上相应格子的分值。每行相邻两数之间用一个空格分隔。

输出
仅一个数，为最小的平方和值。

输入样例1

3
1 1 1 1 1 1 1 3
1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 0
1 1 1 1 1 1 0 3

输出样例1

1460

本题为二维区间dp问题
动归状态 dp[ t ][ i ][ j ][[ k ][ l ]：在(i,j)-(k,l)范围内分割y次的情况下的最小结果。
动归方程
学习笔记——动态规划(全),学习,笔记,动态规划

学习笔记——动态规划(全),学习,笔记,动态规划

代码实现

#include<iostream>
using namespace std;
int arr[10][10]={0};
int dp[20][10][10][10][10]={0};
int VAL(int i,int j,int k,int l)
{
	return arr[k][l]-arr[k][j-1]-arr[i-1][l]+arr[i-1][j-1];
}
int S(int x)
{
	return x*x;
}
int main()
{
	int n;
	cin>>n;
	for(int i=1;i<=8;i++)//求二位前缀和 
	{
		for(int j=1;j<=8;j++)
		{
			cin>>arr[i][j];
			arr[i][j]+=(arr[i-1][j]+arr[i][j-1]-arr[i-1][j-1]);
		}
	}
	for(int i=1;i<=8;i++)//边界条件，t=1的情况 
	{
		for(int j=1;j<=8;j++)
		{
			for(int k=i;k<=8;k++)
			{
				for(int l=j;l<=8;l++)
				{
					dp[1][i][j][k][l]=S(VAL(i,j,k,l));		
				}
			}
		}
	}
	for(int t=2;t<=n;t++)
	{
	for(int i=1;i<=8;i++)
	{
		for(int j=1;j<=8;j++)
		{
			for(int k=i;k<=8;k++)
			{
				for(int l=j;l<=8;l++)
				{
					int ans=0x3f3f3f3f;
					for(int u=i;u<k;u++)
					{
						int val1=dp[t-1][i][j][u][l]+dp[1][u+1][j][k][l];
						int val2=dp[t-1][u+1][j][k][l]+dp[1][i][j][u][l];
						ans=min(ans,min(val1,val2));
					} 
					for(int v=j;v<l;v++)
					{
						int val3=dp[t-1][i][j][k][v]+dp[1][i][v+1][k][l];
						int val4=dp[t-1][i][v+1][k][l]+dp[1][i][j][k][v];
						ans=min(ans,min(val3,val4));
					}
					dp[t][i][j][k][l]=ans;
				}
			}
		}
	}
	}
	cout<<dp[n][1][1][8][8];
	return 0;
}

9.windy数

题目背景

windy 定义了一种 windy 数。

题目描述

不含前导零且相邻两个数字之差至少为 $2$ 的正整数被称为 windy 数。windy 想知道，在 $a$ 和 $b$ 之间，包括 $a$ 和 $b$ ，总共有多少个 windy 数？

输入格式

输入只有一行两个整数，分别表示 $a$ 和 $b$ 。

输出格式

输出一行一个整数表示答案。

样例 #1

样例输入 #1

1 10

样例输出 #1

样例 #2

样例输入 #2

25 50

样例输出 #2

数据规模与约定

对于全部的测试点，保证 $\leq a \leq b \leq 2 \times 10^9$ 。

思路：本题为数位dp问题，这类问题的特征是给定区间[a,b]，求该范围内的符合条件的数有多少个，数据范围比较大，但可以把一位一位数遍历的问题转化为对位数的遍历，这类问题一般有固定的模板。

代码实现

#include<iostream>
#include<cstring>
using namespace std;
int dp[15][15];
int arr[15];
int len=0;
/*pos是当前搜索到的位置，
pre为前一位的数，记录pre的作用是为了判断相差是否小于2，
limit的作用是指示前面是否出现了每一位数都紧贴上界的情况，作用是方便选择当前一位数的取值范围，
zero记录了是否出现前导零的情况 */ 
long long dfs(int pos,int pre,int limit,int zero)
{
	if(pos>len)return 1;
	if(!limit&&dp[pos][pre]!=-1)return dp[pos][pre];//若当前位数没有限制，且已经进行了缓存，则直接return 
	int up=limit?arr[len-pos+1]:9;//根据是否限制来去pos位的最大值 
	long long ret=0;
	for(int i=0;i<=up;i++) 
	{
		if(abs(pre-i)<2)continue;
		if(zero&&i==0)ret+=dfs(pos+1,-2,0,1);//若为前导零 
		else ret+=dfs(pos+1,i,limit&&i==up,0);//不为前导零 
	}
	if(!limit)dp[pos][pre]=ret;//对第一次出现的该情况进行缓存 
	return ret;
}
int solve(long long x)
{
	len=0;
	while(x)arr[++len]=x%10,x/=10;//把每一位取出放到arr上 
	memset(dp,-1,sizeof(dp));
	return dfs(1,-2,1,1);//-2的作用是保证不会出现相差<2的情况 
}
int main()
{
	long long a,b;
	cin>>a>>b;
	//[a,b]范围内的取值等价于[1,b]的取值减去[1,a-1]的取值。 
	long long ret1=solve(a-1);
	long long ret2=solve(b);
	cout<<ret2-ret1<<endl;
	return 0;
 }

10.Round_Numbers

题目描述
Round Numbers 就是一个表示成二进制的时候0比1多或者相等的正数，注意是正数，所以0就肯定不是了。

题目是给定一个区间，问在这个区间上的Round Numbers有多少个？

输入
输入文件包含多个测试数据。

每组测试数据占一行，含有两个整数学习笔记——动态规划(全),学习,笔记,动态规划

输入文件以 EOF 结束。

输出
对于每组测试数据，在单独的一行内输出结果。

输入样例1

2 12

输出样例1

6

数据规模与限定
时间限制：1 s

内存限制：64 M

代码实现

#include<iostream>
#include<cstring>
using namespace std;
int dp[35][35][35];
int arr[35];
int len=0;
long long dfs(int pos,int num0,int num1,int limit,int zero)
{
	if(pos>len&&num0-num1>=0)return 1;
	if(pos>len&&num0-num1<0)return 0;
	if(!limit&&dp[pos][num0][num1]!=-1)return dp[pos][num0][num1];
	int up=limit?arr[len-pos+1]:1;
	long long ret=0;
	for(int i=0;i<=up;i++)
	{
		if(zero&&i==0)ret+=dfs(pos+1,0,0,0,1);
		else ret+=dfs(pos+1,num0+(i==0),num1+(i==1),limit&&i==up,0);
	}
	if(!limit)dp[pos][num0][num1]=ret;
	return ret;
}
long long solve(long long x)
{
	len=0;
	memset(dp,-1,sizeof(dp));
	while(x)arr[++len]=x%2,x/=2;
	return dfs(1,0,0,1,1);
}
int main()
{
	long long L,R;
	cin>>L>>R;
	long long ret1=solve(L-1);
	long long ret2=solve(R);
	cout<<ret2-ret1;
	return 0;
 }

动归优化

1.去除冗余状态

1.乌龟棋

题目描述

小明过生日的时候，爸爸送给他一副乌龟棋当作礼物。

乌龟棋的棋盘是一行 $N$ 个格子，每个格子上一个分数（非负整数）。棋盘第 $1$ 格是唯一的起点，第 $N$ 格是终点，游戏要求玩家控制一个乌龟棋子从起点出发走到终点。

乌龟棋中 $M$ 张爬行卡片，分成 $4$ 种不同的类型（ $M$ 张卡片中不一定包含所有 $4$ 种类型的卡片，见样例），每种类型的卡片上分别标有 $1, 2, 3, 4$ 四个数字之一，表示使用这种卡片后，乌龟棋子将向前爬行相应的格子数。游戏中，玩家每次需要从所有的爬行卡片中选择一张之前没有使用过的爬行卡片，控制乌龟棋子前进相应的格子数，每张卡片只能使用一次。

游戏中，乌龟棋子自动获得起点格子的分数，并且在后续的爬行中每到达一个格子，就得到该格子相应的分数。玩家最终游戏得分就是乌龟棋子从起点到终点过程中到过的所有格子的分数总和。

很明显，用不同的爬行卡片使用顺序会使得最终游戏的得分不同，小明想要找到一种卡片使用顺序使得最终游戏得分最多。

现在，告诉你棋盘上每个格子的分数和所有的爬行卡片，你能告诉小明，他最多能得到多少分吗？

输入格式

每行中两个数之间用一个空格隔开。

第 $1$ 行 $2$ 个正整数 $N, M$ ，分别表示棋盘格子数和爬行卡片数。

第 $2$ 行 $N$ 个非负整数， $a_1,a_2,…,a_N$ ，其中 $a_i$ 表示棋盘第 $i$ 个格子上的分数。

第 $3$ 行 $M$ 个整数， $b_1,b_2,…,b_M$ ，表示 $M$ 张爬行卡片上的数字。

输入数据保证到达终点时刚好用光 $M$ 张爬行卡片。

输出格式

一个整数，表示小明最多能得到的分数。

样例 #1

样例输入 #1

9 5
6 10 14 2 8 8 18 5 17
1 3 1 2 1

样例输出 #1

提示

每个测试点 1s。

小明使用爬行卡片顺序为 $1, 1, 3, 1, 2$ ，得到的分数为 $6 + 10 + 14 + 8 + 18 + 17 = 73$ 。注意，由于起点是 $1$ ，所以自动获得第 $1$ 格的分数 $6$ 。

对于 $30\%$ 的数据有 $1 \leq N \leq 30, 1 \leq M \leq 12$ 。

对于 $50\%$ 的数据有 $1 \leq N \leq 120, 1 \leq M \leq 50$ ，且 $4$ 种爬行卡片，每种卡片的张数不会超过 $20$ 。

对于 $100\%$ 的数据有 $1 \leq N \leq 350, 1 \leq M \leq 120$ ，且 $4$ 种爬行卡片，每种卡片的张数不会超过 $40$ ； $0≤a_i≤100,1≤i≤N,1≤b_i≤4,1≤i≤M$ 。

动归状态 dp[ i ][ j ][ k ][ l ]：在卡片1使用i，卡片2使用j张，卡片3使用k张，卡片4使用l张的情况下所能取得的最大收益。
动归方程
dp[ i ][ j ][ k ][ l ]=max(dp[ i-1 ][ j ][ k ][ l ],dp[ i ][ j-1 ][ k ][ l ],dp[ i ][ j ][ k-1 ][ l ],dp[ i ][ j ][ k ][ l-1 ])+val[ s ] (s=a+2b+3c+4d)
代码实现
去除冗余状态之前

#include<iostream>
using namespace std;
#define MAX_N 350
#define MAX_M 120
int a[MAX_N+5];
int kind[5]={0};
int dp[50][50][50][50]={0};
int main()
{
	int N,M;
	cin>>N>>M;
	for(int i=0;i<N;i++)
	cin>>a[i];
	for(int i=1,x;i<=M;i++)
	{
		cin>>x;
		kind[x]++;	
	}
	dp[0][0][0][0]=a[0];
	for(int i=0;i<=kind[1];i++)
	{
		for(int j=0;j<=kind[2];j++)
		{
			for(int k=0;k<=kind[3];k++)
			{
				for(int l=0;l<=kind[4];l++)
				{
					int ans=0;
					int s=i+2*j+3*k+4*l;
					if(i)ans=max(ans,dp[i-1][j][k][l]);
					if(j)ans=max(ans,dp[i][j-1][k][l]);
					if(k)ans=max(ans,dp[i][j][k-1][l]);
					if(l)ans=max(ans,dp[i][j][k][l-1]);
					dp[i][j][k][l]=ans+a[s];
				}
			}
		}
	}
	cout<<dp[kind[1]][kind[2]][kind[3]][kind[4]];
	return 0;
 }

去除冗余状态之后

#include<iostream>
using namespace std;
#define MAX_N 350
#define MAX_M 120
int a[MAX_N+5];
int kind[5]={0};
int dp[50][50][50]={0};
int main()
{
	int N,M;
	cin>>N>>M;
	for(int i=0;i<N;i++)
	cin>>a[i];
	for(int i=1,x;i<=M;i++)
	{
		cin>>x;
		kind[x]++;	
	}
	dp[0][0][0]=a[0];
	for(int i=0;i<=kind[1];i++)
	{
		for(int j=0;j<=kind[2];j++)
		{
			for(int k=0;k<=kind[3];k++)
			{
				for(int l=0;l<=kind[4];l++)
				{
					int ans=0;
					int s=i+2*j+3*k+4*l;
					if(i)ans=max(ans,dp[j][k][l]);
					if(j)ans=max(ans,dp[j-1][k][l]);
					if(k)ans=max(ans,dp[j][k-1][l]);
					if(l)ans=max(ans,dp[j][k][l-1]);
					dp[j][k][l]=ans+a[s];
				}
			}
		}
	}
	cout<<dp[kind[2]][kind[3]][kind[4]];
	return 0;
 }

2.状态重定义

1.墙壁涂色

例如，当 n=5,k=3 时，下面是一种合法的涂色方案

学习笔记——动态规划(全),学习,笔记,动态规划

而由于墙壁是环形的，所以下面就是一种非法的方案

学习笔记——动态规划(全),学习,笔记,动态规划

输入
输入两个数字 n，k（1≤n≤103，2≤k≤10），分别代表墙壁数量和颜色种类。

输出
对于每个询问，输出一行整数，合法的墙壁涂色方案数。

样例输入1

5 3

样例输出1

30

代码实现
原先版本

#include<iostream>
#include<vector>
using namespace std;
#define MAX_N 1000
#define MAX_K 10
//本题使用大整数版本来实现 
class BigInt:public vector<int>
{
	public:
		BigInt(){push_back(0);}
		BigInt(int x){
			push_back(x);
			proccess_digit();
		}
		BigInt &operator+=(const BigInt&a)
		{
			for(int i=0;i<a.size();i++)
			{
				if(i>=size())push_back(a[i]);
				else at(i)+=a[i];
			}
			proccess_digit();
			return*this;
		}
		BigInt operator+(const BigInt&a)
		{
			BigInt ret(*this);
			ret+=a;
			return ret;
		}
		void proccess_digit()
		{
			for(int i=0;i<size();i++)
			{
				if(at(i)<100000)continue;
				if(i==size()-1)push_back(0);
				at(i+1)+=at(i)/100000;
				at(i)%=100000;
			}
			return ;
		}
};
ostream&operator<<(ostream &out,BigInt &a)
{
	out<<a[a.size()-1]; 
	for(int i=a.size()-2;i>=0;i--)
	{
		for(int j=10000;j>0;j/=10)
		{
			out<<a[i]%(j*10)/j;
		}
	}
	return out;
}
BigInt dp[2][MAX_K+5][MAX_K+5]={0};//滚动数组避免内存超限 
int main()
{
	int n,k;
	cin>>n>>k;
	for(int i=1;i<=k;i++)dp[1][i][i]=1;
	for(int i=1;i<=k;i++)
	{
		for(int j=1;j<=k;j++)
		{
			if(i!=j)dp[0][i][j]=1;
		}
	}
	for(int s=3;s<=n;s++)
	{
		for(int i=1;i<=k;i++)
		{
			for(int j=1;j<=k;j++)
			{
				dp[s%2][i][j]=0;
				for(int l=1;l<=k;l++)
				{	
					if(l==j)continue;
					dp[s%2][i][j]+=dp[(s-1)%2][i][l];
				}
			}
		}
	}
	BigInt ans=0;
	for(int i=1;i<=k;i++)
	{
		for(int j=1;j<=k;j++)
		{
			if(i==j)continue;
			ans+=dp[n%2][i][j]; 
		}
	}
	cout<<ans;
	return 0;
}

优化版本
动归状态 dp[ i ]：前i个位置的最大合法方案数量。
动归方程
dp[ i ]=(k-1)*dp[ i-2 ]+(k-2)*dp[ i-2 ]
前i个位置的最大合法方案数量为第i-1个位置与开头相同的数量以及第i-1个位置与开头不同的数量之和。

初始条件
dp[ 1 ]=k,dp[ 2 ]=k*(k-1),dp[ 3 ]=k*(k-1)*(k-2)

#include<iostream>
#include<vector>
using namespace std;
#define MAX_N 1000
class BigInt : public vector<int>{
public :
    BigInt() { push_back(0); }
    BigInt(int x) {
        push_back(x);
        proccess_digit();
        return ;
    }
    
    BigInt &operator+=(const BigInt &a) {
        for (int i = 0; i < a.size(); i++) {
            if (i < size()) at(i) += a[i];
            else push_back(a[i]);
        }
        proccess_digit();
        return *this;
    }

    BigInt &operator*=(const int x) {
        for (int i = 0; i < size(); i++) at(i) *= x;
        proccess_digit();
        return *this;
    }

    BigInt operator*(const int x) {
        BigInt ret(*this);
        ret *= x;
        return ret;
    }

private :
    void proccess_digit() {
        for (int i = 0; i < size(); i++) {
            if (at(i) < 100000) continue;
            if (i + 1 == size()) push_back(0);
            at(i + 1) += at(i) / 100000;
            at(i) %= 100000;
        }
        return ;
    }
};

BigInt dp[MAX_N]={0};
ostream &operator<<(ostream &out, const BigInt &a) {
    out << a[a.size() - 1];
    for (int i = int(a.size()) - 2; i >= 0; i--) {
        int num = a[i];
        for (int j = 10000; j > 0; j /= 10) {
            out << a[i] % (j * 10) / j;
        }
    }
    return out;
}

int main()
{
	int n,k;
	cin>>n>>k;
	dp[1]=k;
	dp[2]=k*(k-1);
	dp[3]=k*(k-1)*(k-2);
	for(int i=4;i<=n;i++)
	{
		dp[i]=dp[i-1]*(k-2);
		dp[i]+=dp[i-2]*(k-1);
	}
	cout<<dp[n];
	return 0;
}

2.扔鸡蛋

定义鸡蛋的硬度为 k，则代表鸡蛋最高从 k 楼扔下来不会碎掉，现在给你 n 个硬度相同的鸡蛋，楼高为 m，问最坏情况下最少测多少次，可以测出鸡蛋的硬度。

学习笔记——动态规划(全),学习,笔记,动态规划

输入
输入两个数字 n,m（1≤n≤32,1≤m<231），代表 n 个鸡蛋和 m 层楼。

输出
输出一行整数，代表最坏情况下最少测多少次可以测出鸡蛋的硬度。

样例输入1

2 100

样例输出1

14

样例输入2

1 5

样例输出2

5

动归状态： dp[ i ][ j ]:i个鸡蛋测j层楼最多最少需要的次数。
动归方程：
学习笔记——动态规划(全),学习,笔记,动态规划
代码实现：

#include<iostream>
using namespace std;
#define MAX_N 32
#define MAX_M 100000
int dp[MAX_N+5][MAX_M+5]={0};
int main()
{
	int n,m;
	cin>>n>>m;
	for(int i=1;i<=m;i++)
	dp[1][i]=i;
	for(int i=2;i<=n;i++)
	{
		dp[i][1]=1;
		for(int j=2;j<=m;j++)
		{
			dp[i][j]=m;
			for(int k=1;k<=j;k++)
			{
				dp[i][j]=min(dp[i][j],max(dp[i][j-k],dp[i-1][k-1])+1);
			}
		}
	}
	cout<<dp[n][m];
	return 0;
 }

优化版本
动归状态： dp[ i ][ k ]:i个鸡蛋扔k次最少最多能测的楼层数。
动归方程：
学习笔记——动态规划(全),学习,笔记,动态规划

代码实现：

#include<iostream>
using namespace std;
#define MAX_N 32
#define MAX_K 1000
long long dp[MAX_N+5][MAX_K+5]={0};
int main()
{
	long long n,m;
	cin>>n>>m;
	if(n==1)
	{
		cout<<m;
		return 0;
	}
	for(int i=1;i<=1000;i++)
	dp[1][i]=i;
	for(int i=2;i<=n;i++)
	{
		for(int k=1;k<=1000;k++)
		{
			dp[i][k]=dp[i-1][k-1]+dp[i][k-1]+1;
		}
	}
	for(int k=1;k<=1000;k++)
	{
		if(dp[n][k]<m)continue;
		cout<<k;
		break;
	}
	return 0;
 }

3.转移过程

1.切割回文

题目描述
给出一个字符串S，问对字符串S最少切几刀，使得分成的每一部分都是一个回文串（注意：单一字符是回文串）

学习笔记——动态规划(全),学习,笔记,动态规划

输入
一个长度为n(1≤n≤500000)的字符串S，只包含小写字母。

输出
输出一个整数，代表所切的最少刀数。

样例输入

sehuhzzexe

样例输出

4

原做法为区间dp，时间复杂度为O（n3）。

优化

动归状态： dp[ i ]:从1到i位置最少切多少刀。
动归方程：

学习笔记——动态规划(全),学习,笔记,动态规划
代码实现：

#include<iostream>
#include<cstring>
#include<vector>
using namespace std;
#define MAX_N 500000
char arr[MAX_N+5]={0};
int dp[MAX_N+5]={0};
vector<int>c[MAX_N+5];
//记录可以和i位置构成回文串的所有j位置，避免后面的重复计算。
void extract(int i,int j)
{
	while(arr[i]==arr[j])
	{
		c[i].push_back(j);
		i++,j--;
	}
	return ;
}
int main()
{
	cin>>arr+1;
	int len=strlen(arr+1);
	dp[1]=0;
	for(int i=1;i<=len;i++)
	{
		extract(i,i);
		extract(i,i+1);
	 } 
	for(int i=2;i<=len;i++)
	{
		dp[i]=i;
		for(auto j:c[i])
		{
			if(j==1)dp[i]=0;
			else dp[i]=min(dp[i],dp[j-1]+1);
		}
	} 
	cout<<dp[len];
	return 0;
}

2.最长上升子序列

题目描述
有一个数字序列，求其中最长严格上升子序列的长度

学习笔记——动态规划(全),学习,笔记,动态规划

输入
输入一个数字n (1≤n≤1000000)，代表数字序列的长度。

后跟 n 个整数，第 i 个整数 ai(1≤ai≤10000)，代表数字序列中的第 i 个值。

输出
输出一个整数，代表所求的最长严格上升子序列的长度。

样例输入

10
3 2 5 7 4 5 7 9 6 8

样例输出

5

代码实现

#include<iostream>
using namespace std;
#define MAX_N 1000000
#define MAX_K 10000
int dp[MAX_N+5]={0};
int len[MAX_K+5]={0};
int binary_search(int x,int ans)
{
	int head=0,tail=ans,mid;
	while(head<tail)
	{
		mid=(head+tail+1)/2;
		if(len[mid]<x)head=mid;
		else tail=mid-1;
	}
	return head;
}
int main()
{
	int n;
	cin>>n;
	len[0]=-1;
	int ans=0;
	for(int i=1,x;i<=n;i++)
	{
		cin>>x;
		dp[i]=binary_search(x,ans)+1;
		len[dp[i]]=x;
		if(dp[i]>ans)ans=dp[i];
	}
	cout<<ans;
	return 0;
}

3.多重背包

学习笔记——动态规划(全),学习,笔记,动态规划

输入
第一行输入两个数V、n，分别代表背包的最大承重和物品种类数。

接下来 n 行，每行三个数 Vi、Wi、Si，分别代表第 i 种物品的重量、价值和数量。

输出
输出一个整数，代表在背包不超重情况下所装物品的最大价值。

样例输入1

15 4
4 10 5
3 7 4
12 12 2
9 8 7

样例输出1

37

优化1-拆分优化
在原先的做法种中，我们依次枚举了以一种物品中的每一个，但是这种效率比较低，我们可以参考二进制，例如一个数14，我们可以将其拆分为1，2，4，8，7四部分，他们可以组合为任意数，这样一来，我们之前要进行的的14次枚举现在只需要4次。
代码实现

#include<iostream>
using namespace std;
#define MAX_N 100000
int dp[MAX_N+5];
int main()
{
	int V,n;
	cin>>V>>n;
	for(int i=1,v,w,s;i<=n;i++)
	{
		cin>>v>>w>>s;
		for(int k=1;s;s-=k,k*=2)
		{
			k=min(k,s);
			for(int j=V;j>=k*v;j--)
			{
				dp[j]=max(dp[j],dp[j-k*v]+k*w);
			}
		}
	}
	cout<<dp[V];
	return 0;
 }

优化2-单调队列

#include<iostream>
#include<deque>
using namespace std;
#define MAX_V 100000
#define MAX_N 100
int dp[MAX_N+5][MAX_V+5];
int main()
{
	int V,n;
	cin>>V>>n;
	for(int i=1,v,w,s;i<=n;i++)
	{
		cin>>v>>w>>s;
		for(int j=0;j<v;j++)
		{
			deque<int>q;
			for(int k=j;k<=V;k+=v)
			{
				dp[i-1][k]-=k/v*w;
				while(!q.empty()&&dp[i-1][q.back()]<dp[i-1][k])q.pop_back();
				q.push_back(k);
				if((k-q.front())/v>s)q.pop_front();
				dp[i][k]=dp[i-1][q.front()]+k/v*w;
			}
		}
	}
	cout<<dp[n][V];
	return 0;
}

4.矩形

在一个黑白相间的矩形中，问有多少个全白色的子矩形。

学习笔记——动态规划(全),学习,笔记,动态规划

输入
第一行输入两个数字 n,m（2≤n,m≤1000），代表矩形的长和宽。

接下来 n 行，每行 m 个数字，0 代表黑色格子，1 代表白色格子。

输出
输出一个整数，代表全白色子矩形的数量，结果可能过大，输出时请对 100007 取余。

样例输入1

6 6
0 1 1 1 1 1
1 1 0 1 1 1
1 1 1 1 1 1
1 1 1 0 1 1
1 1 1 1 0 1
1 0 1 1 1 1

样例输出1

152

动归状态： dp[ i ][ j ]:以i，j位置开始的矩形的数量。
f[ i ][ j ]:i，j位置即下面的连续白色块数量。
动归方程：
dp[ i ][ j ]=f[ i ][ j ]*(k-j)+dp[ i ][ k ] （k为本行第一个小于f[ i ][ j ]的位置）
代码实现：
优化前

#include<iostream>
using namespace std;
#define MAXSIZE 1000
long long dp[MAXSIZE+5][MAXSIZE+5]={0};
int f[MAXSIZE+5][MAXSIZE+5]={0};
int arr[MAXSIZE+5][MAXSIZE+5];
int main()
{
	int n,m;
	cin>>n>>m;
	for(int i=1;i<=n;i++)
	{
		for(int j=1;j<=m;j++)
		{
			cin>>arr[i][j];
		}
	}
	for(int i=n;i>=1;i--)
	{
		for(int j=1;j<=m;j++)
		{
			if(arr[i][j]==0)
			{
				f[i][j]=0; 
				continue;
			}
			f[i][j]=f[i+1][j]+1;
		}
	}	
	long long ans=0;
	for(int i=1;i<=n;i++)
	{
		for(int j=m;j>=1;j--)
		{
			int len=0;
			for(int k=j;k<=m;k++)
			{
				if(f[i][j]>f[i][k])break;
				len++;
			}
			dp[i][j]=f[i][j]*len+dp[i][j+len];
			dp[i][j]%=100007;
			ans+=dp[i][j];
			ans%=100007;
		}
	}

	cout<<ans;
	return 0;
}

优化-单调栈（维护最近小于关系）

#include<iostream>
#include<stack>
using namespace std;
#define MAXSIZE 1000
long long dp[MAXSIZE+5]={0};
int f[MAXSIZE+5][MAXSIZE+5]={0};
int arr[MAXSIZE+5][MAXSIZE+5];
int main()
{
	int n,m;
	cin>>n>>m;
	for(int i=1;i<=n;i++)
	{
		for(int j=1;j<=m;j++)
		{
			cin>>arr[i][j];
		}
	}
	for(int i=n;i>=1;i--)
	{
		for(int j=1;j<=m;j++)
		{
			if(arr[i][j]==0)
			{
				f[i][j]=0; 
				continue;
			}
			f[i][j]=f[i+1][j]+1;
		}
	}	
	long long ans=0;
	for(int i=1;i<=n;i++)
	{
		stack<int>s;
		f[i][m+1]=-1;
		s.push(m+1);
		for(int j=m;j>=1;j--)
		{
			while(f[i][s.top()]>=f[i][j])s.pop();
			dp[j]=f[i][j]*(s.top()-j)+dp[s.top()];
			dp[j]%=100007;
			ans+=dp[j];
			ans%=100007;
			s.push(j);
		}
	}
	cout<<ans; 
	return 0;
}

4.斜率优化

1.古老的打字机

题目描述
有一台古老的打字机和一篇待打印的文章，文章中有 n 个字符，每个字符会有一个消耗值 Ci, 打字机工作一次会打印若干连续的 k 个字符，同时打字机会有磨损，打字机的单次磨损计算公式为：

学习笔记——动态规划(全),学习,笔记,动态规划

其中 M 是打字机启动一次的固定磨损值，现在给你 n 个字符的消耗值，问你打字机顺序打印出这 n 个字符的最小磨损值为多少？

输入
第一行输入两个数字，n,M(1≤n≤106,1≤M≤104) 代表文章中字符数量和打字机单次启动的固定磨损值。

第二行输入 n 个数字，第 i 个数字代表文章中第 i 个字符的磨损值 Ci(1≤Ci≤100)。

输出
输出一个整数，代表打字机顺序打完 n 个字符的最小磨损值

样例输入1

6 40
3 3 6 5 1 2

样例输出1

256

思路：如果我们使用常规的思路，很容易会想到将状态定义为dp[ i ]:前i个数字的最小磨损值。
学习笔记——动态规划(全),学习,笔记,动态规划
但是此时的时间复杂度为O(n2),会超时。
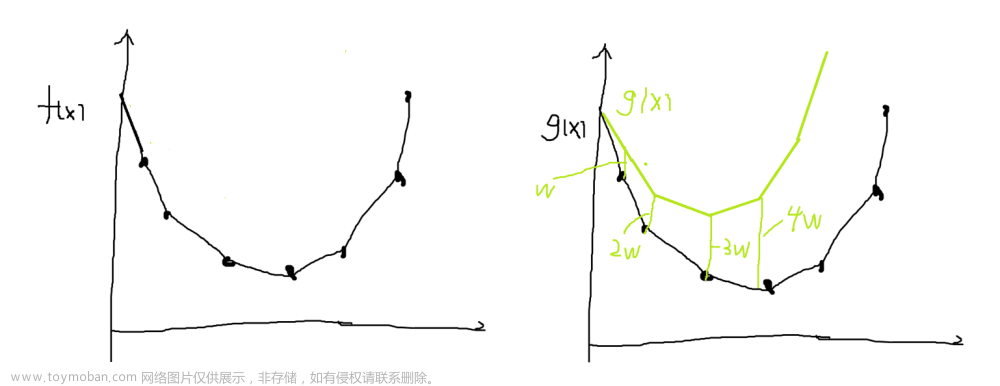
优化策略：我们将dp[ i ]的公式拆开，得到：

查找值是可以记录的，确定值是一个常数，只有混合值是可变的，如果没有混合值，那么时间复杂度可以降低为O(n),如何可以消除混合值的影响？
学习笔记——动态规划(全),学习,笔记,动态规划

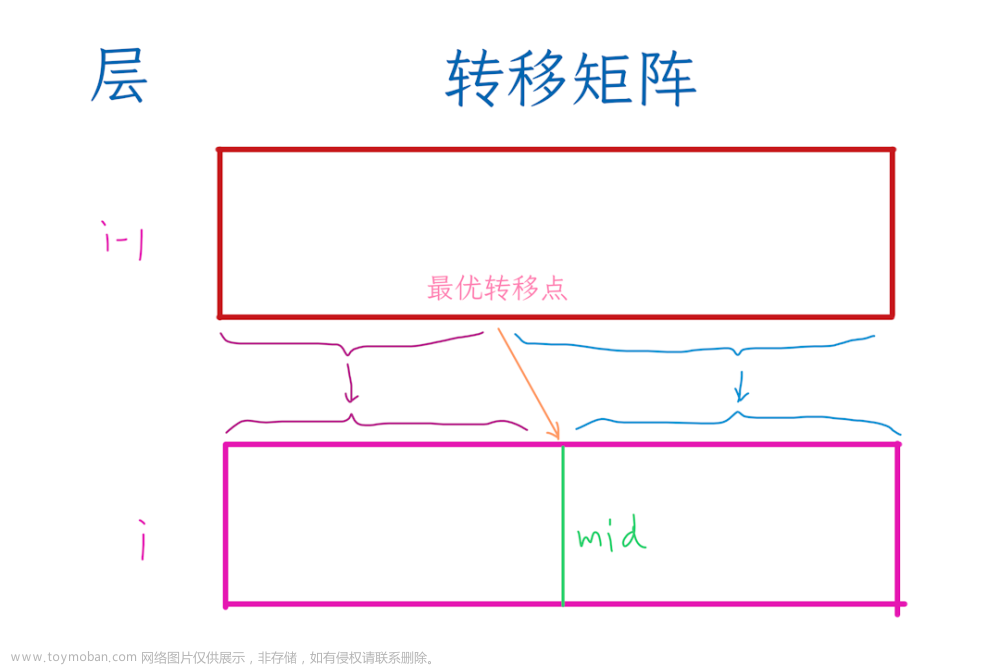
由此可以看出，只要呈现出上图的情况，k一定不是候选答案，可直接删除。

因此，备选答案的集合一定是这个样子，现在我们要怎么在上面的集合中找到备选值呢？

据此可以分析出，找到第一个大于2sum[ i ]斜率的g(x,y),x就是最终应选的值。
代码实现：文章来源地址https://www.toymoban.com/news/detail-838892.html

#include<iostream>
using namespace std;
#define MAX_N 1000000
#define SQ(a) ((a)*(a))
long long dp[MAX_N+5];
int q[MAX_N+5];
long long f[MAX_N+5];
long long sum[MAX_N+5];
long long n,M;
double slope(int a,int b)
{
	return (1.0*(f[a]-f[b]))/(1.0*(sum[a]-sum[b]));
}
void set(int a,int b)
{
	dp[b]=dp[a]+SQ(sum[b]-sum[a])+M;
	f[b]=dp[b]+SQ(sum[b]);
	return ;
}
int main()
{
	cin>>n>>M;
	int head=0,tail=0;
	q[tail++]=0;
	sum[0]=0;
	for(int i=1;i<=n;i++)
	{
		cin>>sum[i];
		sum[i]+=sum[i-1];
	}
	for(int i=1;i<=n;i++)
	{
		while(tail-head>=2&&slope(q[head],q[head+1])<2*sum[i])head++;
		set(q[head],i);
		while(tail-head>=2&&slope(q[tail-1],q[tail-2])>slope(q[tail-1],i))tail--;
		q[tail++]=i;
	}
	cout<<dp[n];
	return 0;
}