变换矩阵 (Transformation Marices) ,一切物体的缩放,旋转,位移,都可以通过变换矩阵作用得到,在光栅化中会用到,同时在投影 (projection) 变换也有很多应用
将如下图所示的简单矩阵乘法定义为对向量的线性变换。
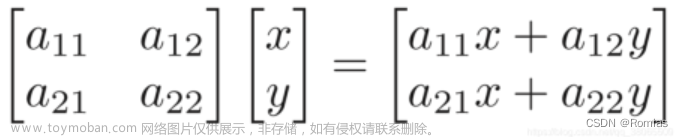
最简单的缩放变换,如图,即除了(0,0)不变之外都乘以某个系数

矩阵形式:

反射操作:(即关于y轴翻转)

切变(shearing):
把物体一边固定,然后拉另外一边,如图

分别对应"拉伸"x轴,和"拉伸"y轴
(变换通用方法:找对应点分析坐标的转换形式)

旋转Rotate(默认以原点为中心,逆时针旋转):重要的变换矩阵

同上,通过对应点坐标(1,0)(0,1)变换后关系可确定变换矩阵

补充:旋转角度-a和a其实是相反操作,因为旋转矩阵的逆矩阵等于他的转置 是正交矩阵

总结:
变换总能写成相同维度矩阵乘向量形式,如果能写成,就叫他线性变换

为什么强调相同维度?

如图,平移变换比较特殊,无法矩阵化,不是线性变换,只能写成以下形式:

为了不搞特殊,统一所有变换到一块用一种方法表示,引入齐次坐标:
(简单来说就是为了能用矩阵乘向量统一表示所有变换,多加一维)

注:最后一维为1,表示点(point), 为0表示方向(direction)
现在我们就可以用一个矩阵既表示线性变换(先),又表示位移(后)
为什么是1,0?为了保持向量的平移不变性,任何一个点都写成(x,y,1),任何一个向量都写成(x,y,0)
如下图所示,这种设置还有更多的考虑,齐次坐标系下:
向量加向量还是向量,点减去点是向量,点加向量得到一个新的点,点加上点是这两个点的中点,如图

引入齐次坐标后所有的仿射变换(一个向量空间进行一次线性变换并接上一个平移)都可以写成齐次坐标的形式:

同理,其他变换的齐次坐标系形式:

逆变换:M-1

变换回原来的形状,即逆变换,数学上就是乘以对应变换的逆矩阵
(这也是用矩阵乘法表示变换的优点之一,可以方便地描述逆变换)
复杂变换可以通过一系列简单变换得到,变换的顺序很重要(因为矩阵乘法没有交换律,先旋转后平移和先平移后旋转得到的结果不一样)

如图,注意是从右往左计算,如果应用太多矩阵可以写作以下形式(结合律的应用),即一个矩阵可以表示多次的复杂变换经过

同理变换不仅能合成也能分解(从右到左):围着任意轴旋转可以如图考虑

三维变换

如图,同理用二维做类比,向量(x,y,z,w)实质上是表示在空间中坐标为(x/w,y/w,z/w)的点

注意这样是先变换再平移
如图,类似二维,如果W不为0,则默认(x,y,z,w)表示的是三维空间中坐标为(x/w,y/w,z/w)的点

齐次坐标系下的三维变换:

平移和缩放:

旋转(较为复杂)关于某个坐标轴变换:(关于的轴对应坐标不用变化,“绕谁谁不变”,其余两个轴对应坐标参考二维旋转)
注意绕y时相反,因为此时根据右手螺旋定则是z叉乘x,而旋转矩阵的行列式对应关系是x向z转的,需要反一下

类似二维,任意旋转都是正交矩阵,因此他们的逆是他们的转置,如逆时针转30°,转置就是顺时针30°
以上都是绕单独坐标轴旋转,而任意一个3D旋转都可以写成分别绕XYZ轴旋转操作的组合:

其中αβγ角又被称为欧拉角 例:roll滚转(机身左右旋转) pitch俯仰(上下抬头) yaw偏航(平行的左右)

由此引出了罗德里格斯Rodrigues旋转公式:图形学中
α为旋转角 I为单位矩阵 n为环绕的某个轴的方向,即一个旋转向量(nx,ny,nz)(此时默认起点是过原点的轴)N为由n得到的一个反对称矩阵
R即为某个向量V以n方向为轴旋转α度后得到的向量Vrot要经过的旋转矩阵 即Vrot=RV,旋转前的向量坐标乘以R等于旋转后的向量坐标

如果要沿着任意轴,需要先将轴平移,以过原点的为轴再旋转,再整体平移回去
四元数:引入更多是为了计算旋转与旋转之间的差值,因为用矩阵表示旋转不方便计算,机器人学中用的比较多
四元数可以很方便地表示旋转变换。但在很多场合中,使用矩阵形式和向量形式表达旋转更有利于推导,因此这里不再赘述
另注:罗德里格斯公式推导的个人理解

该公式有多种推导方法,我观看的视频讲解如图,向量V绕k旋转θ角得到的向量Vrot
我们需要推导的就是这两个之间的关系,即经过的变换矩阵
那么首先由平行四边形法则可得,原向量V可以看作是分别在旋转轴k方向的分向量V∥和垂直于k轴的方向上的分向量V⊥之和
同理旋转后得到的向量Vrot也可以是V∥和垂直于k轴的方向上的分向量Vrot⊥之和,我们就从这点出发来找关系:
由向量点乘公式可得,用原向量V和单位向量k点乘来表示V在k方向上的投影长度,再乘以k的方向就可以表示V∥
由平行四边形法则可得,V⊥=V-V∥,又由叉乘的定义可得V⊥=-kx(kxv),即与v和k都垂直的单位向量c再叉乘-k得到与-k和c都垂直的向量V⊥
同理,Vrot⊥是通过正交分解求的,Vrot⊥在旋转的过程中长度不变(始终等于V⊥),因此V⊥的模乘以cosθ就是Vrot⊥在红色面上的投影长度,再把这个长度乘以V⊥方向的单位向量(b)就是Vrot⊥在红色面上的分量【同理也可以是(|b| = cos(PI -θ ) |V⊥| = (- cosθ)|V⊥|),再乘以V⊥相反方向】,同理相似的另外一个分量就乘以sinθ,两个分量相加就是Vrot⊥文章来源:https://www.toymoban.com/news/detail-838893.html
之后经过代换简化就可得到罗德里格斯公式。文章来源地址https://www.toymoban.com/news/detail-838893.html
到了这里,关于图形学学习笔记1:基础变换矩阵的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!