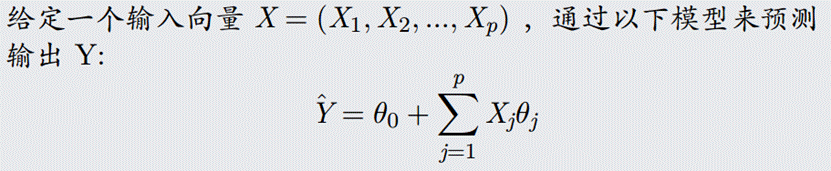**背景:**2D/3D激光雷达扫描的点云数据,拟合直线做分析,实现总共有三种方法:
(1)PCL点云库实现
(2)利用标准库手写
(3)不使用任何库,链表方式实现
使用手写实现的主要目的是因为程序可能会在性能一般的单片机(不支持库)上跑。
第一种方式可看本人激光雷达处理系列中一篇文章:https://blog.csdn.net/qq_37967853/article/details/133946558?spm=1001.2014.3001.5502
接下来主要介绍另外两种方法:
1.标准库手写
struct Point {
double x;
double y;
};
// 定义拟合直线的模型
struct Line {
double slope;
double intercept;
};
// 计算两点之间的距离
double distance(Point p1, Point p2) {
double dx = p2.x - p1.x;
double dy = p2.y - p1.y;
return sqrt(dx * dx + dy * dy);
}
constexpr double TOLERANCE = 1.0; // 用于计算直线拟合的容差值
constexpr int MAX_ITERATIONS = 100; // RANSAC算法的最大迭代次数
constexpr int MIN_POINTS = 5; // 拟合直线所需的最小点数
constexpr int MIN_INLIERS = 20; // 拟合直线所需的最小内点数
// 生成随机数
double generateRandomNumber(double min, double max) {
return min + static_cast<double>(std::rand()) / (RAND_MAX / (max - min));
}
// RANSAC拟合直线
Line ransac(const std::vector<Point>& points) {
std::srand(std::time(nullptr)); // 初始化随机种子
Line bestLine;
int bestInliers = 0;
for (int i = 0; i < MAX_ITERATIONS; ++i) {
// 随机选择两个点
int index1 = std::rand() % points.size();
int index2 = std::rand() % points.size();
while (index2 == index1) {
index2 = std::rand() % points.size();
}
const Point& p1 = points[index1];
const Point& p2 = points[index2];
// 计算直线参数
double slope = (p2.y - p1.y) / (p2.x - p1.x);
double intercept = p1.y - slope * p1.x;
// 统计内点数
int inliers = 0;
for (const Point& p : points) {
double d = std::abs(p.y - slope * p.x - intercept);
if (d < TOLERANCE) {
++inliers;
}
}
// 更新最优直线
if (inliers > bestInliers && inliers >= MIN_INLIERS) {
bestInliers = inliers;
bestLine.slope = slope;
bestLine.intercept = intercept;
}
}
return bestLine;
}
int main() {
std::srand(std::time(nullptr)); // 初始化随机种子
// 生成随机点
std::vector<Point> points;
for (int i = 0; i < 100; ++i) {
double x = generateRandomNumber(-10.0, 10.0);
double y = 2.0 * x + generateRandomNumber(-1.0, 1.0); // 两条直线的斜率分别为2和-2
points.push_back({ x, y });
}
std::vector<Point> points1;
for (int i = 0; i < 100; ++i) {
double x = generateRandomNumber(-10.0, 10.0);
double y = -2.0 * x + generateRandomNumber(-1.0, 1.0); // 两条直线的斜率分别为2和-2
points1.push_back({ x, y });
}
points.insert(points.end(), points1.begin(), points1.end());
// RANSAC拟合直线
std::vector<Line> lines;
while (points.size() >= MIN_POINTS) {
Line line = ransac(points);
lines.push_back(line);
// 从数据中移除拟合的内点
std::vector<Point> remainingPoints;
for (const Point& p : points) {
double d = std::abs(p.y - line.slope * p.x - line.intercept);
if (d >= TOLERANCE) {
remainingPoints.push_back(p);
}
}
points = remainingPoints;
}
// 输出拟合结果
for (int i = 0; i < lines.size(); i++) {
std::cout << "拟合直线 " << i + 1 << " 方程:y = " << lines[i].slope << "x + " << lines[i].intercept << std::endl;
}
return 0;
}
结果:
2.不使用任何库,利用链表数据结构
std只是用来随机数生成点云数据的,算法部分涉及的随机生成算法是自己实现的。详细实现看代码注释。
using namespace std;
//点数据
struct Node {
double x;
double y;
Node* next;
};
//直线参数
struct LineNode {
double slope;
double intercept;
LineNode* next;
};
//随机数生成算法
unsigned int xorshift32()
{
static unsigned int state = 2463534242; // 初始种子
unsigned int x = state;
x ^= x << 13;
x ^= x >> 17;
x ^= x << 5;
state = x;
return x;
}
//计算两点x之间最大值(横向最远)
//寻找链表中x的极值
double findMaxDist(Node* head) {
double xmax=0;
double xmin=0;
Node* current = head;
while (current != nullptr) {
if ( current->x < xmin) {
xmin = current->x;
}
if (current->x > xmax) {
xmax = current->x;
}
current = current->next;
}
return xmax - xmin;
}
//释放链表内存,在链表使用结束
template<typename T>
void deleteNodeList(T* head) {
while (head != nullptr) {
T* temp = head;
head = head->next;
delete temp;
}
}
template<typename T>
void deleteArryNodeList(T* lines[]) {
// 释放数组链表中的内存
int size = sizeof(lines) / sizeof(lines[0]);
for (int i = 0; i < size; i++) {
if (lines[i] != nullptr) {
deleteNodeList(lines[i]);
}
}
}
//向链表末尾添加数据
void addNode(Node*& head, double x, double y) {
if (head == nullptr) {
Node* node = new Node;
node->x = x;
node->y = y;
node->next = nullptr;
head = node;
}
else {
Node* temp1 = head;
while (temp1->next != nullptr) {
temp1 = temp1->next;
}
temp1->next = new Node;
temp1->next->x = x;
temp1->next->y = y;
temp1->next->next = nullptr;
}
}
//向链表末尾添加数据
void addLineNode(LineNode*& head, double slope, double intercept) {
if (head == nullptr) {
LineNode* node = new LineNode;
node->slope = slope;
node->intercept = intercept;
node->next = nullptr;
head = node;
}
else {
LineNode* temp1 = head;
while (temp1->next != nullptr) {
temp1 = temp1->next;
}
temp1->next = new LineNode;
temp1->next->slope = slope;
temp1->next->intercept = intercept;
temp1->next->next = nullptr;
}
}
//合并链表
//将链表1加在链表2后面,顺序不变
void appendList(Node*& list1, Node* list2) {
if (list1 == nullptr) {
list1 = list2;
}
else {
Node* temp = list1;
while (temp->next != nullptr) {
temp = temp->next;
}
temp->next = list2;
}
}
//链表1赋值替换链表2
void replaceList(Node* list1, Node*& list2) {
// 释放链表 list2 的内存
while (list2 != nullptr) {
Node* temp = list2;
list2 = list2->next;
delete temp;
}
// 复制链表 list1 的节点到 list2
Node* current = list1;
Node* head_1 = nullptr;//head_1为head_1链表的头节点地址
while (current != nullptr) {
Node* newNode = new Node;
newNode->x = current->x;
newNode->y = current->y;
newNode->next = nullptr;
if (head_1 == nullptr) {
head_1 = newNode;
}
else {
Node* temp = head_1;
while (temp->next != nullptr) {//循环遍历head_1链表(中已存放的newNode)
temp = temp->next;//找到末尾的空地址
}
temp->next = newNode;//新newNode数据添加到已存放的newNode末尾
}
current = current->next;
}
list2 = head_1;//将head_1链表首地址赋值给list2首地址,指针的值复制
}
//计算链表size
template<typename T>
int getListSize(T*& head) {
int size = 0;
T* current = head;
while (current != nullptr) {
size++;
current = current->next;
}
return size;
}
// 从链表中随机选择节点
Node* getRandomNode(Node* head) {
int length = getListSize(head);
// 生成随机数种子
std::srand(static_cast<unsigned int>(std::time(nullptr)));
// 生成随机索引
int randomIndex = std::rand() % length;
Node* current = head;
for (int i = 0; i < randomIndex; i++) {
current = current->next;
}
return current;
}
template<typename T>
void printList(T* head) {
T* temp = head;
while (temp != nullptr) {
std::cout << "(" << temp->x << ", " << temp->y << ") ";
temp = temp->next;
}
std::cout << std::endl;
}
// 获取链表中特定索引位置的指针
Node* getValueAtIndex(Node* head, int index) {
Node* temp = head;
int currentIndex = 0;
while (temp != nullptr) {
if (currentIndex == index) {
return temp; // 返回节点的值(或你想要获取的值)
}
temp = temp->next;
currentIndex++;
}
return nullptr;
// 如果索引超出链表长度,可以根据具体情况进行错误处理
// 在此示例中,我们返回一个默认值 -1.0
/*return -1.0;*/
}
constexpr double TOLERANCE = 2.0; // 用于计算直线拟合的容差值
constexpr int MAX_ITERATIONS = 100; // RANSAC算法的最大迭代次数
constexpr int MIN_POINTS = 15; // 拟合直线所需的最小点数
constexpr int MIN_INLIERS = 20; // 拟合直线所需的最小内点数
// 生成随机数
double generateRandomNumber(double min, double max) {
return min + static_cast<double>(std::rand()) / (RAND_MAX / (max - min));
}
// RANSAC拟合直线
LineNode* ransac(Node*& points) {
std::srand(std::time(nullptr)); // 初始化随机种子
//Line bestLine;
LineNode* bestLine = nullptr;
int bestInliers = 0;
int size = getListSize(points);
for (int i = 0; i < MAX_ITERATIONS; ++i) {
//随机从链表中选择两个不相同的点,生成随机数种子
//生成随机索引
unsigned int randomIndex1 = xorshift32() % size;
Node* randomNode1 = getValueAtIndex(points, randomIndex1);
unsigned int randomIndex2 = xorshift32() % size;
while (randomIndex1 == randomIndex2) {
randomIndex2 = xorshift32() % size;
}
Node* randomNode2 = getValueAtIndex(points, randomIndex2);
// 统计内点数
int inliers = 0;
double slope = 0;
double intercept = 0;
// 计算直线参数
if (randomNode1 != nullptr && randomNode2 != nullptr) {
slope = (randomNode2->y - randomNode1->y) / (randomNode2->x - randomNode1->x);
intercept = randomNode1->y - slope * randomNode1->x;
Node* current = points;
while (current != nullptr) {
double d = std::abs(current->y - slope * current->x - intercept);
if (d < TOLERANCE) {
++inliers;
}
current = current->next;
}
// 内点数最多的直线,更新最优直线
if (inliers > bestInliers && inliers >= MIN_INLIERS) {
bestInliers = inliers;
addLineNode(bestLine, slope, intercept);
}
}
}
cout << "bestInliers:" << bestInliers << endl;
return bestLine;
}
int main() {
std::srand(std::time(nullptr)); // 初始化随机种子
// 生成随机点
Node* points = nullptr;
for (int i = 0; i < 100; ++i) {
double x = generateRandomNumber(-10.0, 10.0);
double y = 2.0 * x + generateRandomNumber(-1.0, 1.0); // 两条直线的斜率分别为2和-2
addNode(points, x, y);
}
Node* points1 = nullptr;
for (int i = 0; i < 100; ++i) {
double x = generateRandomNumber(-10.0, 10.0);
double y = -2.0 * x + generateRandomNumber(-1.0, 1.0); // 两条直线的斜率分别为2和-2
addNode(points1, x, y);
}
appendList(points, points1);
printList(points);
//线段最长的
double max_line_length = 0;
//循环计数
int index = 0;
//符合墙面线要求的索引,方便求出符合要求的直线
int model_index=0;
//RANSAC拟合直线,假设提前知道在一百条以内
LineNode* lines[100];
int points_Size = 0;
points_Size=getListSize(points);
while (points_Size >= MIN_POINTS) {//循环条件
cout << "points变化size"<<index<<":" << points_Size << endl;
LineNode* line = ransac(points);
//如果拟合不出直线则退出
if (line==nullptr) {
break;
}
cout << "best" << line->slope << " " << line->intercept << endl;
lines[index]=line;
//外点,从数据中移除拟合的内点
Node* remainingPoints = nullptr;
//内点,提取内点
Node* interiorPoint = nullptr;
for (Node* current = points; current!=nullptr ; current=current->next)
{
double d = std::abs(current->y - line->slope * current->x - line->intercept);
if (d >= TOLERANCE) {
addNode(remainingPoints, current->x, current->y);
}
else {
addNode(interiorPoint, current->x, current->y);
}
}
int interiorPoint_Size = getListSize(interiorPoint);
cout << "内点数目" << interiorPoint_Size << endl;
int remainingPoints_Size = getListSize(remainingPoints);
cout << "外点数目" << remainingPoints_Size<< endl;
//寻找内点中最大和最小的点
double maxdist=findMaxDist(interiorPoint);
cout << "横向最大距离" << maxdist << endl;
//内点求满足一定范围斜率且横向长度最长的
//if (-tan(45)<line->slope<tan(45) && maxdist> max_line_length) {
// max_line_length = maxdist;
// model_index = index;
//}
//计算符合条件的直线方程
if (0 < abs(line->slope) && maxdist> max_line_length) {
max_line_length = maxdist;
model_index = index;
}
//若没有外点则退出循环
if (remainingPoints==nullptr) {
break;
}
replaceList(remainingPoints,points);
cout << "------------" << endl;
points_Size = getListSize(points);
index++;
}
std::cout << "目标直线方程:y = " << lines[model_index]->slope << "x + " << lines[model_index]->intercept << std::endl;
//清除链表内存,即使没有通过new
deleteNodeList(points);
deleteNodeList(points1);
deleteArryNodeList(lines);
上述代码对于ransac每次拟合出来的直线参数链表,我们存储在假设内存为100大小的数组中,实际上不严谨,因为事先并不知道会拟合出多少条直线,因此此处可以再定义一个结构体链表来存储多条直线参数链表(大链表中存储一系列小链表)。
//存放直线参数链表的大链表
struct LineNodes
{
NodeList::LineNode* L;
LineNodes* next;
};
//向大链表中添加一系列小链表
template<typename T>
void addLineNodes(LineNodes*& head,T* L) {
if (head == nullptr) {
LineNodes* node = new LineNodes;
node->L = L;
node->next = nullptr;
head = node;
}
else {
LineNodes* temp1 = head;
while (temp1->next != nullptr) {
temp1 = temp1->next;
}
temp1->next = new LineNodes;
temp1->next->L = L;
temp1->next->next = nullptr;
}
}
main中:
LineNodes* linenodes=nullptr;//替换原来的LineNode* lines[100];
nodelist.addLineNodes(linenodes, line);//替换原来的lines[index]=line;
//打印
LineNodes* linenode = nodelist.getValueAtIndex(linenodes, model_index);
std::cout << "目标直线方程:y = " << linenode->L->slope<< "x + " << linenode->L->intercept << std::endl;
//释放
nodelist.deleteNodeList(linenodes);
结果:
**注意:**对于第二种方法,实现过程中一定要注意指针为空的情况,指针为空时会报错:读取访问权限错误。另外拟合直线时,一定要对数据有初步认识,最好先去除离群点再来拟合,容差设置尤为关键,太小可能会拟合不出直线,太大会导致得到的直线不准确。文章来源:https://www.toymoban.com/news/detail-838966.html
以上代码均为本人手敲加调试实现,完成不易,转载或引用请注明出处。文章来源地址https://www.toymoban.com/news/detail-838966.html
到了这里,关于利用C++实现RANSAC拟合多条直线并提出符合要求的直线,标准库和手写(不使用任何库、链表方式)两种方法的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!