动态规划入门篇——斐波那契数列与爬楼梯问题-Toy模板网

这篇具有很好参考价值的文章主要介绍了动态规划入门篇——斐波那契数列与爬楼梯问题。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

一、认识动态规划

动态规划（Dynamic Programming，简称DP）是运筹学的一个分支，也是求解多阶段决策过程最优化问题的一种方法。它主要用来解决一类最优化问题，通过将复杂问题分解成若干个子问题，并综合子问题的最优解来得到原问题的最优解。动态规划的核心在于对问题的状态进行定义和描述状态之间的关系，使得问题能够以递推（或者说分治）的方式解决。

简称DP，在解决算法问题中，如果这个问题是由多个子问题重叠，那么使用动态规划来解决问题是最好的选择，它的每一个状态都需要上一个状态推导而成。

二、如何去完成动态规划类的问题

大家多多少少都有了解，动态规划关键是递推公式，所以有人就会认为背下几个递推公式就足以完成算法题目，显然不是如此。在一些基础的算法题可能有效，但是遇上了有难度的题目可能就有些不够用了。

了解动态规划的递推公式固然重要，但不仅仅于此。

那么有以下四步做题关键非常重要，

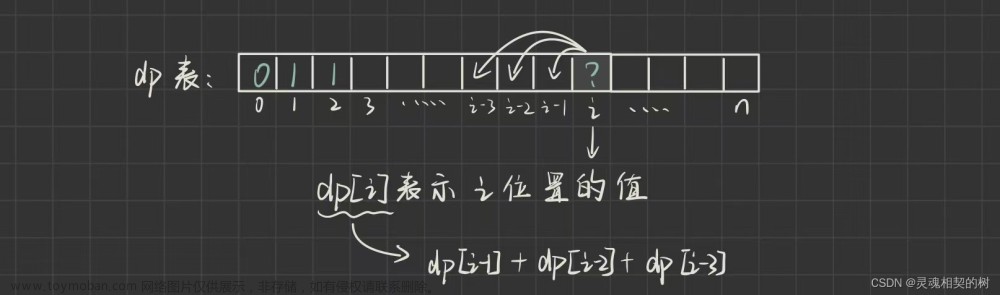
1.确定动态数组，也就是dp[ ],以及其下标的意义

2.明确动态公式

3.数组的初始化

4.遍历顺序的确定

就算知道了递推公式，不了解其数组含义，还有遍历顺序，那么这题多半也是很难做下去！

三、斐波那契数列

初识这个问题，想必都是在函数递归时接触到，一道非常基础入门的题目，作为动态规划的入门也是极为合适。

斐波那契数，由F(n)表示。该数列由0和1开始，后面的每一项数字都是前面两项之和，即 F(0) = 0 ,F(n) = 1,F(n) = F(n-1) +F(n-2),给出n，计算出F(n)。

在这里就不做过多的分析，直接利用前文的四个做题步骤

1.明确dp数组和下标的意义

那么在本题，dp[ i ]的含义为斐波那契数列的第i个数的值。

2.明确解题公式

题目中已经很明确的说出公式，因此为dp[ i ] = dp[ i - 1 ] + dp [ i - 2].

3.数组初始化

题目也已经给出，dp[ 0 ] = 0,dp[ 1 ] = 1.

4.确定遍历顺序

dp[ i ] 得出结果需要依靠dp[ i - 1 ]和dp[ i - 2 ]来实现，所以遍历的顺序是从前往后遍历。

代码如下:

int fit(int n)
    {
        if(n <= 1)
           return n;
        vector<int> dp(n);
        dp[0] = 0;
        dp[1] = 1;
        for(int i = 2;i <= n;i++)
        {
            dp[i] = dp[i-1] + dp[i-2];
        }
            return dp[n];
    }

完成初步的了解后，还可以对此题解进行优化，我们观察到该递归公式，只需要关注dp[i-1]和dp[i-2]两个数即可，那么我们只需记录两个数就够了，然后利用这两个数层层往后推导，不需要记录整个数列。

优化后代码：

int fit(int n)
  {
     if( n <= 1)
     return n;
     int dp[2];
     dp[0] = 0;
     dp[1] = 1;
     for(int i = 2;i<=n;i++)
       {
         int a = dp[0] + dp[1];
         dp[0] = dp[1];//利用两个变量来承接上一层循环的结果
         dp[1] = a;
        }

    return a;
    }

四、爬楼梯问题

假如你现在正在爬楼梯，需要爬n阶才能到楼顶。你每一步可以爬一到两个台阶，那么你有几种方法能到达楼顶呢？

其实这道题也能分解成一个个的子问题，刚开始接触可能确实不太好想，那如果试着一阶一阶的来往后递推，就会很好思考，例如爬上第一阶只需要迈一步，那么就只有一种方法，而第二层那要么就是从第一层迈一层，或者在第0层迈两层，就有了两种方法，那么第三层呢，就需要从第一层的状态和第二层推导出来，所以就可以说，到达第三层的方法是第一层和第二层的方法数的和。其实这样一分析，这个题目其实是斐波那契数列的一个拓展。

接下来还是按照四个步骤往下走，

1.明确dp数组和其下标的含义

与斐波那契数一样，这里的dp[i]是指到达第i个阶梯，有多少种方法

2.明确递推公式

与斐波那契数一样，公式为dp[i] = dp[i-1] + dp[i-2]，由下面阶层的方法累加出上面阶层的方法数。

3.初始化

在此题有一个很尴尬的地方，那就是对于第0层的方法数的看法不一，题目的见解大家各有千秋，那么这里就打算使用dp[1]和dp[2]来作为初始化的两个值

dp[1] = 1,dp[2] = 2。

4.确定遍历顺序

还是与斐波那契数列一样，这里的循环条件需要由前面的子问题来累加出来得出结果，所以是一个从前往后的循环条件。

代码如下：

int climb(int n)
    {
        if (n<=1)
        return n;
        vector<int> dp(n);
        dp[1] = 1;
        dp[2] = 2;
        for(int i = 3;i <= n ;i++）
        {
            dp[i] = dp[i - 1]+dp[i - 2];
        }
            return dp[i];
        }

那么这道题的优化方法依旧与上题一样，不再过多赘述。

此题还可以更改很多类型的爬楼梯问题，例如可以一口气爬1，2，3层楼梯，以及爬一层楼梯我需要耗费多少力气，那么爬到顶需要耗费多少力气？大家可以多去钻研！

文章来源地址https://www.toymoban.com/news/detail-839540.html

到了这里，关于动态规划入门篇——斐波那契数列与爬楼梯问题的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！