作者推荐
视频算法专题
预备知识
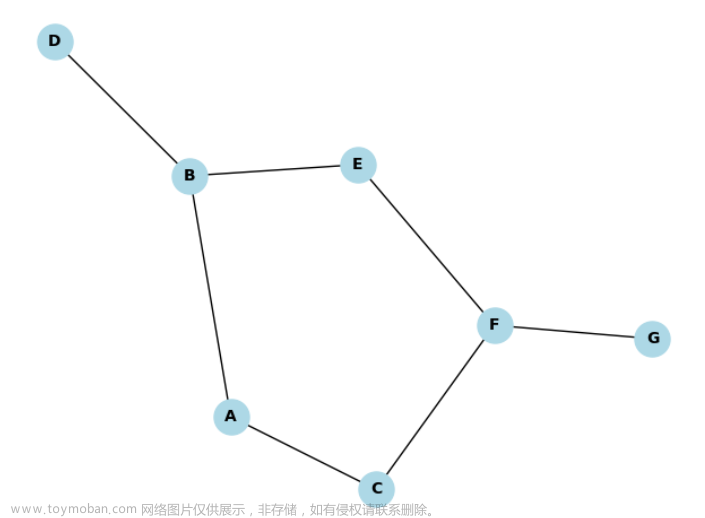
本分析针对:连通无向图G。
搜索树
节点的父子关系:任意 节点的邻接 节点除了已处理 节点,都是它的子 节点。 以任意一点为根开始DFS,计算所有 节点的父子关系。只保留个子 节点到父 节点形成边,形成的树是搜索树。搜索树上的边是树边,非树边是回边。
节点级别,根节点级别0,它的子节点级别1,它的孙节点级别2。
cur子树:搜索树中,以cur为根的子树。
cur子图:dfs(cur) ,依次dfs(next各子节点)。整个dfs过程,所有cur
→
\rightarrow
→ next 形成的边组成的子图简称cur子树。dfs(next)前,如果next已编号(分配时间戳、访问、处理),则不是子节点。
时间戳
计算搜索树上时,各节点的时间顺序,我的习惯是从0开始。伪代码如下:
m_iTime=0
DFS( cur)
{
cur的时间戳是m_iTime++。
for(next: cur的未编号邻接点)
{
dfs(next)
}
}
若干性质
性质一: 搜索树上的两点连通,则对应的图一定连通。因为:搜索树有的边,对应的图都有。
性质二:搜索树上,假定一个节点n1有m个子节点,则删除n1和相关边后,有1+m个连通区域。各子节点各一个连通区域,其它节点一个连通区域(简称根子树)。根据性质一,对应的图最多1+m个连通区域。
性质三:dfs(c1)前,c1到c10的某条路径全部是未访问节点,则dfs(c1)时一定会访问c10。
令在这条路径上:c1的后继点是c2,c2是c3,c3是c4
⋯
\cdots
⋯
第一次处理c1时,c1处理完c2的哥哥节点后,如果c2未处理,则处理c2,故c2一定会被处理。
第一次处理c2时,c2处理完c3的哥哥节点后,如果c3未处理,则处理c3,故c3一定会被处理。
⋮
\vdots
⋮
性质四:从两个兄弟子树c1,c2的各选择一个节点c11和c21,他们在原图中,要么不连通;要么任何从c11开始到c21结束的路径一定包括他们的某个公共祖先节点。换种说法:c11和c21如果连通,一定经过他们的公共祖先。
性质四1:令两个兄弟子树的父亲节点是搜索树的根(级别0),假定存在若干组兄弟子树不符合性质四,不失一般性,假定c1这些组子树中最年长,即c1和它的哥哥子树不连通,删除它所有的哥哥子树。 因为c1和c11存在不过经过根节点的路径,c11和c21存在不经过根节点的路径,故c1到c21存在不经过根节点的路径。由于c1是最年长的哥哥节点,故dfs(c1)之前,只有根节点已处理,故c1到c21是全部未处理的路径,根据性质三,dfs(c1)是会处理c21,故c21和c1是一棵子树。与假设矛盾。
性质四2:如果某节点cur级别小于等于leve,符合性质四。则级别为leve+1的节点也符合性质四。
如果c11到c21的某条路径经过cur子树以外的节点c31,则必定经过c31和cur的公共祖先,必定是c11和c21的公共祖先,符合性质四。
如果不经过cur子树以外的节点,则删除cur子树外的所有节点。问题就变成性质四1。
判断割点
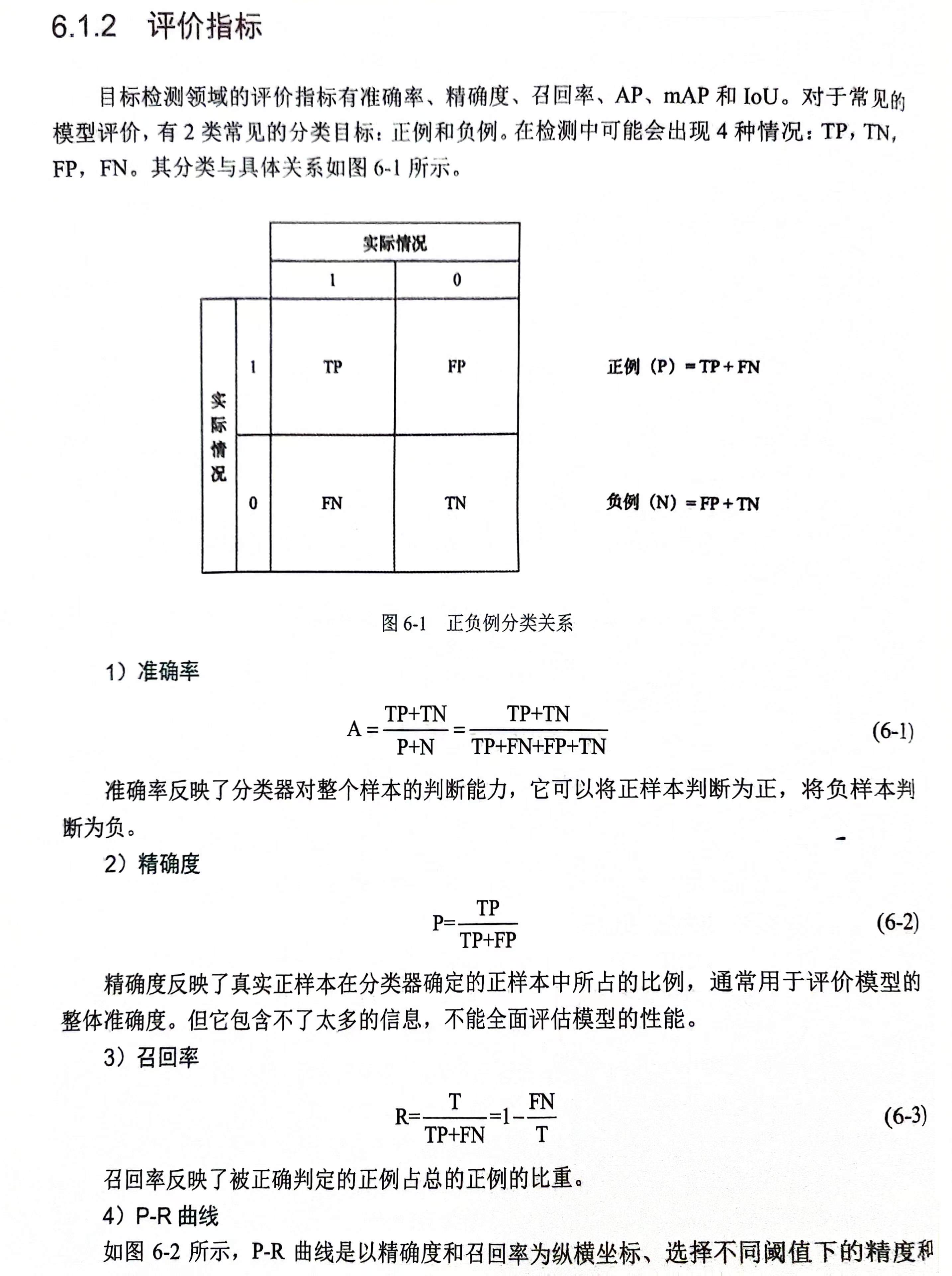
在一个无向图中,如果删除一个节点(顶点)及相关联的边后,图的连通区域(分量)增加。则此节点是割点。
性质五
dfs(cur) 返回 本次dfs直接或间接dfs各节点的时间戳最小值。dfs(cur) 是节点类型(以cur等于6为例),节点类型:
一,cur的祖先节点,部分访问,紫色显示。
二,cur的祖先节点的哥哥子树,访问完成,红色显示。
三,cur的祖先节点的弟弟子树,没有开始访问,蓝色显示。
排除next已经访问,DFS的返回值,分如下几种情况:
一,只访问了本子树,如DFS(3) ,等于time[next]。必定和根子树不连通。
二,只访问了本子树,本子树和cur有两个或以上条边相连,如6和12都和2相连。返回值time[cur]。必定和根子树不连通。
三,访问了紫,dfs(next)是这些点和cur的最早公共祖先的最小时间戳。如果返回值是time[cur],则说明next子树和cur子树外的节点全部通过cur,删除cur后,无法和根子树连通。如果小于time[cur]则表示和根子树连通。
四,根据性质四,访问红蓝节点必定经过紫点,而紫点都已经访问,故在访问到红蓝点之前DFS会结束。
推论:以绿点为起点的边,终点要么是绿点,要么是紫点。即要么是树边,回边(非树边)一定指向它祖宗。
性质六:
假设存在不经过cur,存在从next到某个pub的路径,则一定可以FDS到。如果此路径经过多个pub ,删除第一pub后面的边。因为:因为dfs一个和dfs多个pub的结果一样。假设不经过cur,性质五证明不经过红色蓝色,pub只有一个且在最后,其它节点都是绿点。根据性质三,最后一个绿点一定会访问,访问的时候一定会dfs到此pub。
判断割点的代码
时间复杂度O(n)+O(m)。n是顶点数,m是边数。每个顶点只会dfs一次,每次dfs会循环所有临接点。
【分类讨论】【割点】1568. 使陆地分离的最少天数
如果有多个连通区域,同一个连通区域的时间戳是连续的,故用m_vRegionFirstTime 记录每个连通区域的最小时间戳。m_vCutNewRegion[c]如果存在[left,r) 表示割掉c后,时间戳[left,r)的节点会形成新区域
m_vNodeToTime 各节点的时间戳。
//割点
class CCutPoint
{
public:
CCutPoint(const vector<vector<int>>& vNeiB) : m_iSize(vNeiB.size())
{
m_vNodeToTime.assign(m_iSize, -1);
m_vCutNewRegion.resize(m_iSize);
for (int i = 0; i < m_iSize; i++)
{
if (-1 == m_vNodeToTime[i])
{
m_vRegionFirstTime.emplace_back(m_iTime);
dfs(vNeiB, i, -1);
}
}
}
int dfs(const vector<vector<int>>& vNeiB,const int cur, const int parent)
{
int iMinTime = m_vNodeToTime[cur] = m_iTime++;
int iRegionCount = (-1 != parent);//根连通区域数量
for (const auto& next : vNeiB[cur]) {
if (-1 != m_vNodeToTime[next]) {
iMinTime = min(iMinTime, m_vNodeToTime[next]);
continue;
}
const int childMinTime = dfs(vNeiB, next, cur);
iMinTime = min(iMinTime, childMinTime);
if (childMinTime >= m_vNodeToTime[cur]) {
iRegionCount++;
m_vCutNewRegion[cur].emplace_back(m_vNodeToTime[next], m_iTime);
}
}
if (iRegionCount < 2)
{
m_vCutNewRegion[cur].clear();
}
return iMinTime;
}
const int m_iSize;
const vector<int>& Time()const { return m_vNodeToTime; }//各节点的时间戳
const vector<int>& RegionFirstTime()const { return m_vRegionFirstTime; }//各连通区域的最小时间戳
vector<bool> Cut()const {
vector<bool> ret;
for (int i = 0; i < m_iSize; i++)
{
ret.emplace_back(m_vCutNewRegion[i].size());
}
return ret; }//是否是割点
protected:
vector<int> m_vNodeToTime;
vector<int> m_vRegionFirstTime;
vector < vector<pair<int, int>>> m_vCutNewRegion; //m_vCutNewRegion[c]如果存在[left,r) 表示割掉c后,时间戳[left,r)的节点会形成新区域
int m_iTime = 0;
};
判断割点后,两点是否连通
增加函数判断割点后,两个点是否连通,每次调用时间复杂度O(logn),内部用到了二分查找。
【广度优先搜索】【网格】【割点】1263. 推箱子
获取:指定割点将所在连通区域,分割成若干个子连通区域。时间复杂度:O(n)。
【树上倍增】【割点】 【换根法】3067. 在带权树网络中统计可连接服务器对数目
代码
class CCutPoint
{
public:
CCutPoint(const vector<vector<int>>& vNeiB) : m_iSize(vNeiB.size())
{
m_vNodeToTime.assign(m_iSize, -1);
m_vCutNewRegion.resize(m_iSize);
for (int i = 0; i < m_iSize; i++)
{
if (-1 == m_vNodeToTime[i])
{
m_vRegionFirstTime.emplace_back(m_iTime);
dfs(vNeiB, i, -1);
}
}
}
int dfs(const vector<vector<int>>& vNeiB,const int cur, const int parent)
{
int iMinTime = m_vNodeToTime[cur] = m_iTime++;
int iRegionCount = (-1 != parent);//根连通区域数量
for (const auto& next : vNeiB[cur]) {
if (-1 != m_vNodeToTime[next]) {
iMinTime = min(iMinTime, m_vNodeToTime[next]);
continue;
}
const int childMinTime = dfs(vNeiB, next, cur);
iMinTime = min(iMinTime, childMinTime);
if (childMinTime >= m_vNodeToTime[cur]) {
iRegionCount++;
m_vCutNewRegion[cur].emplace_back(m_vNodeToTime[next], m_iTime);
}
}
if (iRegionCount < 2)
{
m_vCutNewRegion[cur].clear();
}
return iMinTime;
}
const int m_iSize;
const vector<int>& Time()const { return m_vNodeToTime; }//各节点的时间戳
const vector<int>& RegionFirstTime()const { return m_vRegionFirstTime; }//各连通区域的最小时间戳
vector<bool> Cut()const {
vector<bool> ret;
for (int i = 0; i < m_iSize; i++)
{
ret.emplace_back(m_vCutNewRegion[i].size());
}
return ret; }//
const vector < vector<pair<int, int>>>& NewRegion()const { return m_vCutNewRegion; };
protected:
vector<int> m_vNodeToTime;
vector<int> m_vRegionFirstTime;
vector < vector<pair<int, int>>> m_vCutNewRegion; //m_vCutNewRegion[c]如果存在[left,r) 表示割掉c后,时间戳[left,r)的节点会形成新区域
int m_iTime = 0;
};
class CConnectAfterCutPoint
{
public:
CConnectAfterCutPoint(const vector<vector<int>>& vNeiB) :m_ct(vNeiB)
{
m_vTimeToNode.resize(m_ct.m_iSize);
m_vNodeToRegion.resize(m_ct.m_iSize);
for (int iNode = 0; iNode < m_ct.m_iSize; iNode++)
{
m_vTimeToNode[m_ct.Time()[iNode]] = iNode;
}
for (int iTime = 0,iRegion= 0; iTime < m_ct.m_iSize; iTime++)
{
if ((iRegion < m_ct.RegionFirstTime().size()) && (m_ct.RegionFirstTime()[iRegion] == iTime))
{
iRegion++;
}
m_vNodeToRegion[m_vTimeToNode[iTime]] = (iRegion - 1);
}
}
bool Connect(int src, int dest, int iCut)const
{
if (m_vNodeToRegion[src] != m_vNodeToRegion[dest])
{
return false;//不在一个连通区域
}
if (0 == m_ct.NewRegion()[iCut].size())
{//不是割点
return true;
}
const int r1 = GetCutRegion(iCut, src);
const int r2 = GetCutRegion(iCut, dest);
return r1 == r2;
}
vector<vector<int>> GetSubRegionOfCut(const int iCut)const
{//删除iCut及和它相连的边后,iCut所在的区域会分成几个区域:父节点一个区域、各子节点 一个区域
//父节点所在区域可能为空,如果iCut所在的连通区域只有一个节点,则返回一个没有节点的 区域。
const auto& v = m_ct.NewRegion()[iCut];
vector<int> vParen;
const int iRegion = m_vNodeToRegion[iCut];
const int iEndTime = (iRegion + 1 == m_ct.RegionFirstTime().size()) ? m_ct.m_iSize : m_ct.RegionFirstTime()[iRegion+1];
vector<vector<int>> vRet;
for (int iTime = m_ct.RegionFirstTime()[iRegion],j=-1; iTime < iEndTime; iTime++)
{
if (iCut == m_vTimeToNode[iTime])
{
continue;
}
if ((j + 1 < v.size()) && (v[j + 1].first == iTime))
{
j++;
vRet.emplace_back();
}
const int iNode = m_vTimeToNode[iTime];
if ((-1 != j ) && (iTime >= v[j].first) && (iTime < v[j].second))
{
vRet.back().emplace_back(iNode);
}
else
{
vParen.emplace_back(iNode);
}
}
vRet.emplace_back();
vRet.back().swap(vParen);
return vRet;
}
protected:
int GetCutRegion(int iCut, int iNode)const
{
const auto& v = m_ct.NewRegion()[iCut];
auto it = std::upper_bound(v.begin(), v.end(), m_ct.Time()[iNode], [](int time, const std::pair<int, int>& pr) {return time < pr.first; });
if (v.begin() == it)
{
return v.size();
}
--it;
return (it->second > m_ct.Time()[iNode]) ? (it - v.begin()) : v.size();
}
vector<int> m_vTimeToNode;
vector<int> m_vNodeToRegion;//各节点所在区域
const CCutPoint m_ct;
};

扩展阅读
视频课程
有效学习:明确的目标 及时的反馈 拉伸区(难度合适),可以先学简单的课程,请移步CSDN学院,听白银讲师(也就是鄙人)的讲解。
https://edu.csdn.net/course/detail/38771
如何你想快
速形成战斗了,为老板分忧,请学习C#入职培训、C++入职培训等课程
https://edu.csdn.net/lecturer/6176
相关
下载
想高屋建瓴的学习算法,请下载《喜缺全书算法册》doc版
https://download.csdn.net/download/he_zhidan/88348653
| 我想对大家说的话 |
|---|
| 闻缺陷则喜是一个美好的愿望,早发现问题,早修改问题,给老板节约钱。 |
| 子墨子言之:事无终始,无务多业。也就是我们常说的专业的人做专业的事。 |
| 如果程序是一条龙,那算法就是他的是睛 |
测试环境
操作系统:win7 开发环境: VS2019 C++17
或者 操作系统:win10 开发环境: VS2022 C++17
如无特殊说明,本算法用**C++**实现。文章来源:https://www.toymoban.com/news/detail-839986.html
 文章来源地址https://www.toymoban.com/news/detail-839986.html
文章来源地址https://www.toymoban.com/news/detail-839986.html
到了这里,关于割点原理及封装好的割点类的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!