平面型二连杆机器人位形空间RRT避障轨迹规划（MATLAB）-Toy模板网

这篇具有很好参考价值的文章主要介绍了平面型二连杆机器人位形空间RRT避障轨迹规划（MATLAB）。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

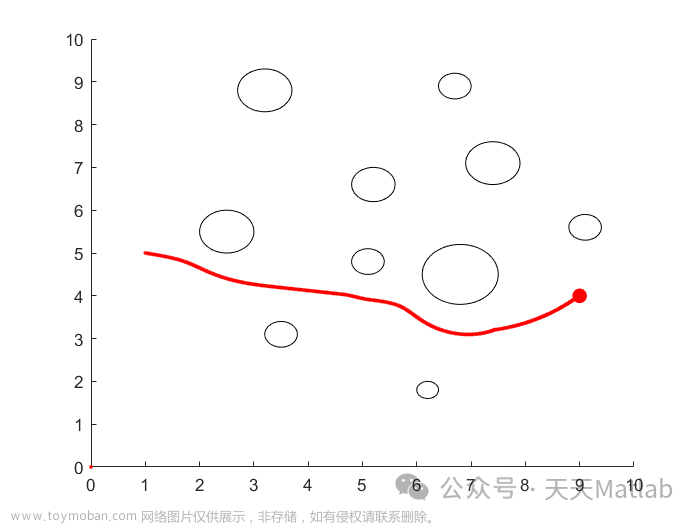
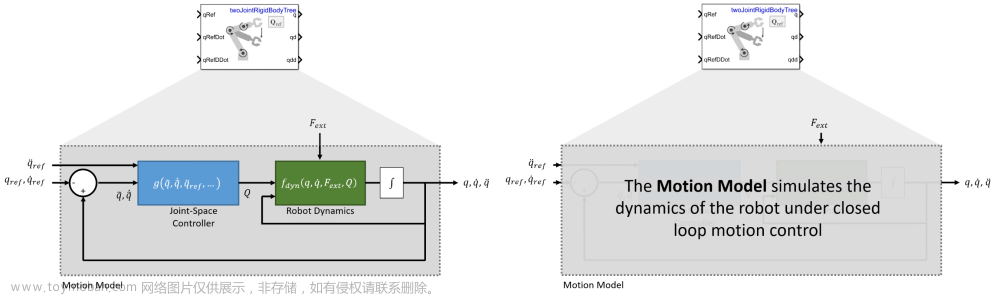
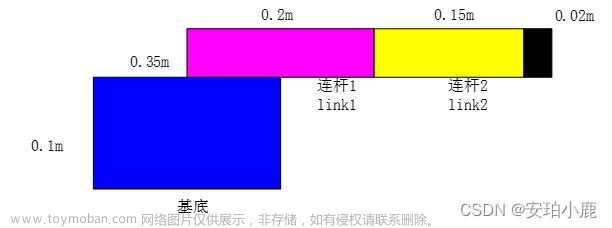
最近在《机器人建模与控制》上看到利用位形空间的避障方法，因此突发奇想做了一个平面型二连杆机器人在位形空间中RRT避障轨迹规划demo。在此做一个记录。

在路径规划中，机器人各点位置的一个完整规范被称为位形（configuration）。位形空间（configuration space），有时也称构型空间，是由机器人所有可能位形所组成的集合。对于二连杆平面型机器人可以用来表示，其中和分别为平面型机器人两个连杆的关节角度，可以想象，这两个参数一旦确定，机器人的位形，或者通俗来说位姿也唯一确定，因此这两个参数可以构成机器人的位形空间。

利用位形空间进行避障，即在位形空间中表示出障碍物空间，从而得到一个可行位形空间。在这个可行空间内进行路径规划，得到一条从起点到终点且不穿过障碍物的轨迹，再将该轨迹转换到工作空间中，即可得到机器人在工作空间中的避障轨迹。

因此该仿真的总体步骤分为：

初始化；
利进行位形空间采样，得到位形空间图；
用RRT算法在位形空间图中得到一条可行路径；
将RRT规划路径转换为机器人关节路径；
可视化整个过程。

1. 初始化

在初始化过程中，主要定义连杆长度、机器人初始坐标、底座坐标和终点坐标。并定义障碍物集合，这里使用cell存储各个障碍物的顶点。在这里还需要进行一些初始判断，例如判断机器人底座是否位于障碍物内，以及可以对终点和起点坐标是否位于障碍物中进行判断。

%% 定义初始变量
link = [0.9,1.2]; %机器人连杆长度
theta_init = [0,-3.14];     %机器人关节初始角度，逆时针转动为正
% theta_init = [-3.14,-3.14];     %机器人关节初始角度，逆时针转动为正
pos_robot_base = [0,0];     %机器人底座坐标
pos_robot_goal = [0.2314,1.1871]; %机器人目标坐标

theta_init = (theta_init<0)*2*pi + theta_init; % 将theta_init转到0-2pi区间内

% 障碍物坐标，定义为cell
pos_barrier_all = {...
                   [0.8,1;1,1;1,0.5;0.8,0.4;0.7,0.5],... %障碍物坐标（这里为五个顶点）
                   [0,-1;-1,-1;-1,-0.5;0,-0.5],...  %障碍物坐标（这里为四个顶点）
                   [0.3,1;0.3,0.5;0,0.5;0,1],...  %障碍物坐标（这里为四个顶点）
                  }; 

% 判断机器人底座位置或目标位置是否位于障碍物内
for k = 1:length(pos_barrier_all)
    pos_barrier = cell2mat(pos_barrier_all(k));
    [in,on] = inpolygon([pos_robot_base(1);pos_robot_goal(1)],[pos_robot_base(2);pos_robot_goal(2)],pos_barrier(:,1),pos_barrier(:,2));
    if any(in) || any(on)
        error('机器人底座位置或目标位置位于障碍物内'); 
    end
end

2. 采样位形空间图

理论上对于凸障碍物在位形空间中的表达有高效的处理方法，但这里简单起见不做考虑。采用最直接的采样方法，即将机器人关节角度离散化，对每一个角度分别进行障碍物判断，构建整张位形空间图。

因为构建位形空间图比较耗时，这里设置了一个判断，当已经存在可用的位形空间图时，设置参数直接调用位形空间图即可。

%% 采样位形空间图
if_use_load_file = 1;     % 判断是否使用mat文件导入位形空间图
if if_use_load_file
    map_file = 'configuration_space_map.mat';
    load(map_file);
else
    configuration_space_step =0.002;  % 位形空间图采样步长
    configuration_space_map = ones(floor(1/configuration_space_step)+1,floor(1/configuration_space_step)+1);
    for i = 0:floor(1/configuration_space_step)
        for j = 0:floor(1/configuration_space_step)
            theta_i = i*2*pi*configuration_space_step;
            theta_j = j*2*pi*configuration_space_step;
            theta1 = theta_i;
            theta2 = theta_j;
            x1 = pos_robot_base(1) + link(1) * cos(theta1);
            y1 = pos_robot_base(2) + link(1) * sin(theta1);
    
            x2 = x1 + link(2) * cos(theta1 + theta2);
            y2 = y1 + link(2) * sin(theta1 + theta2);
            
            pos_robot = [pos_robot_base;x1,y1;x2,y2];
            % 判断机器人与障碍物是否碰撞
            for k = 1:length(pos_barrier_all)
                pos_barrier = cell2mat(pos_barrier_all(k));
                flag=checkCollision(pos_barrier,pos_robot,link);
                if flag 
                    configuration_space_map(i+1,j+1) = 0;
                end
            end
        end    
    end
    configuration_space_map=logical(configuration_space_map);
    save('configuration_space_map.mat','configuration_space_map','configuration_space_step');
end

figure;
imshow(configuration_space_map)

这里采用的判断是否碰撞障碍的方法是看机械臂两连杆与障碍物边界是否相交，若不相交，且机器人底座位于障碍物外，则不碰撞。也可采用RRT所使用的碰撞检测方法，即将机械臂连杆划分为若干点，分别判断这些点是否位于障碍物内。障碍碰撞函数如下：

%% checkCollision.m
% ************************************************************************
% 判断机械臂是否会碰上障碍。
% 这里使用的方法是看机械臂两连杆与障碍物边界是否相交，若不相交，且机器人底座位于障碍物外，则不碰撞。
% 也可采用RRT所使用的碰撞检测方法，即将机械臂连杆划分为若干点，分别判断这些点是否位于障碍物内。
% ************************************************************************
function flag = checkCollision(pos_barrier,pos_robot,link)
flag = false;
size_barrier = size(pos_barrier,1);
size_link = length(link);
for k = 0:size_barrier-1
    for h = 1:size_link
        isIntersect = checkIntersection(pos_robot(h,:),pos_robot(h+1,:),...
        pos_barrier(mod(k,size_barrier)+1,:),pos_barrier(mod(k+1,size_barrier)+1,:));
        if isIntersect
            flag = isIntersect;
            break;
        end
    end  
    if flag
        break;
    end
end
end

最终得到二连杆机器人的位形空间图如下。

平面型二连杆机器人位形空间RRT避障轨迹规划（MATLAB）,平面,机器人,matlab

得到位形空间图后，可以判断起点和终点坐标是否位于障碍物内。

theta_goal = invKine(link,pos_robot_base,pos_robot_goal);
pos_theta_goal = floor(theta_goal/(2*pi)/configuration_space_step)+1;

pos_theta_init = floor(theta_init/(2*pi)/configuration_space_step)+1;

% 二连杆机器人共两种可能目标机器人位型。
% 从后往前删去数据，可保证删去数据后的位型数组数据序号仍保持不变。
for i = 2:-1:1
    % 删除不合条件的机器人位型
    if ~feasiblePoint(pos_theta_goal(i,:),configuration_space_map)
        theta_goal(i,:) = [];
        pos_theta_goal(i,:) = [];
    end
end

if isempty(pos_theta_goal)
    error('机器人目标位姿将碰撞障碍物，请重新设置目标位姿');
end

if ~feasiblePoint(pos_theta_init,configuration_space_map)
    error('机器人初始位姿将碰撞障碍物，请重新设置初始位姿');
end

3. RRT生成避障轨迹

RRT避障主要参考https://www.cnblogs.com/21207-iHome/p/7210543.html中的实现方式。考虑到机器人关节角度与实际上是相同的，即机器人位形空间中上下边界和左右边界是相连的，因此对RRT算法进行一些修改，使其能够越过边界进行搜索，修改方法详见代码，不再赘述。

主程序中对两种可能的终点位形均进行搜索，分别搜索20次，只要找到10次可行路径就跳出循环，取最短路径作为最终的避障路径。

%% RRT搜索路径
RRT_loop_amount = 20;  % 进行RRT搜索的次数，循环找到路径最小值
result_amount = 10;     % 找到规定数量个有效路径后跳出循环
path_final = [];
path_length_final = -1; 
theta_path_final = [];


for i = 1:size(theta_goal,1)
    source = floor(theta_init/(2*pi)/configuration_space_step)+1;
    goal = pos_theta_goal(i,:);
    result_count = 0;
    for j = 1:RRT_loop_amount
        fprintf('RRT loop %d :',j);
        [path,path_length,theta_path,RRT_step,RRT_final_step] = RRT(source,goal,configuration_space_map);
        if path_length_final ==-1 || path_length < path_length_final
            path_final = path;
            path_length_final = path_length;
            theta_path_final = theta_path;
        end
        if path_length ~= inf
            result_count = result_count + 1;            
        end
        if result_count >= result_amount
            break;            
        end
    end
end
if path_length_final ==-1 || path_length_final == inf
    error('没有找到路径');
else
    fprintf('寻找到较优可行路径，路径长度为：%d',path_length_final);
end

%% 显示机器位形空间及规划路径
figure;
imshow(configuration_space_map);
rectangle('position',[1 1 size(configuration_space_map,2)-1 size(configuration_space_map,1)-1],'edgecolor','k');
for i = 1:length(path_final)-1
    if abs(atan2(path_final(i+1,1)-path_final(i,1),path_final(i+1,2)-path_final(i,2)) - theta_path_final(i+1))<1e-1
        pl = line(path_final(i:i+1,2),path_final(i:i+1,1));
        pl.Color = 'red';
        pl.LineStyle = '--';
    else
        pl = line([path_final(i,2); path_final(i,2)+RRT_step * cos(theta_path_final(i+1))],[path_final(i,1); path_final(i,1)+RRT_step * sin(theta_path_final(i+1))]);
        pl.Color = 'red';
        pl.LineStyle = '--';
        pl = line([path_final(i+1,2); path_final(i+1,2)-RRT_step * cos(theta_path_final(i+1))],[path_final(i+1,1); path_final(i+1,1)-RRT_step * sin(theta_path_final(i+1))]);
        pl.Color = 'red';
        pl.LineStyle = '--';
    end
end

% 将RRT规划路径转换为机器人关节路径
robot_path = getRobotPath(path_final,theta_path_final,configuration_space_step,RRT_step,RRT_final_step,size(configuration_space_map,1));

%% RRT.m
% ************************************************************************
% RRT求解可行路径。
% 参考：https://www.cnblogs.com/21207-iHome/p/7210543.html
% ************************************************************************
function [path, pathLength,thetaPath,stepSize,finalStepSize] = RRT(source,goal,map)
finalStepSize = 0;
stepSize = (length(map)-1)/15;  % 每一步RRT生长长度
threshold = stepSize/2; % 两点相隔距离多少近似认为为同一点
maxFailedAttempts = 1000;
display = true; % RRT可视化
RRTreeTotalCount = 500; % 当RRT结点超过最大上限时，认为没有找到路径
RRTreeCount = 1;
RRTree = zeros(RRTreeTotalCount,length(source)+2);
RRTree(1,:) = [source 0 -1]; % RRT根节点 [像素坐标 从父节点到该节点的角度值 节点编号]

failedAttempts = 0;
counter = 0;
pathFound = false;
if display
    imshow(map);
end
while failedAttempts <= maxFailedAttempts  % RRT生成循环
    if rand < 0.5                      % 越大越随机，越小越倾向于直接朝着目标方向运动
        sample = rand(1,2) .* size(map);
    else
        sample = goal;
    end

    [min_dist,vir_sample_all]= distanceCost(RRTree(1:RRTreeCount,1:2),sample,map);
    [~, I] = min(min_dist ,[],1); 
    closestNode = RRTree(I(1),1:2);
    vir_sample = vir_sample_all(I(1),:);
    theta = atan2(vir_sample(1)-closestNode(1),vir_sample(2)-closestNode(2));  
    newPoint = double(int32(closestNode(1:2) + stepSize * [sin(theta)  cos(theta)])); % 此时新生成的点可能在地图边界外，实际上的点应该经过边界回到地图内
    if ~checkPath(closestNode(1:2), newPoint, map) % 如果到达新生成的点会经过障碍物，则排除
        failedAttempts = failedAttempts + 1;
        continue;
    end
    
     % 将新生成的点恢复到地图内
    newPointbefore = newPoint;
	newPoint = (newPoint<=0).*size(map) + newPoint;
    newPoint = -(newPoint>size(map)).*size(map) + newPoint;
        [~, I2] = min( distanceCost(RRTree(1:RRTreeCount,1:2),newPoint,map) ,[],1); % 如果RRT中已存在与新生成的点相近的点，则排除
    if distanceCost(RRTree(I2(1),1:2),newPoint,map) < threshold
        failedAttempts = failedAttempts + 1; 
        continue;
    end
      
    RRTreeCount = RRTreeCount +1;
    RRTree(RRTreeCount,:) = [newPoint theta I(1)]; % 将新的点添加至RRT树中
    failedAttempts = 0;
	% distanceCost(RRTree(1:RRTreeCount,1:2),goal,map)
    if distanceCost(newPoint,goal,map) < threshold % 如果新生成的点与目标点相近，则认为达到目标点
        theta = atan2(goal(1)-newPoint(1),goal(2)-newPoint(2));
        finalStepSize = distanceCost(newPoint,goal,map);
        if ~checkPath(newPoint, goal, map) % 如果到达新生成的点会经过障碍物，则排除
            failedAttempts = failedAttempts + 1;
            continue;
        else          
            I(1) = RRTreeCount;
            RRTreeCount = RRTreeCount +1;
            RRTree(RRTreeCount,:) = [goal theta I(1)]; % 将新的点添加至RRT树中   
            I(1) = RRTreeCount;
            pathFound = true;
        end
    end 
	
    
    if display
        displayNode = closestNode;
        if newPointbefore == newPoint           
            line([displayNode(2);newPoint(2)],[displayNode(1);newPoint(1)])
        else % 针对连通情况的地图连线做了更改。由于框定了地图显示范围，地图外的连线不显示，因此当两点相连需要经过边界的情况，增加了两个辅助点位用于连线。
            line([displayNode(2);newPointbefore(2)],[displayNode(1);newPointbefore(1)]) 
            line([displayNode(2)+newPoint(2)-newPointbefore(2);newPoint(2)],[displayNode(1)+newPoint(1)-newPointbefore(1);newPoint(1)])
        end
        counter = counter + 1;
        M(counter) = getframe;         
    end % Capture movie frame 
    if pathFound
        break;
    end
    if RRTreeCount >= RRTreeTotalCount
        break;
    end
end

% if display
%     disp('click/press any key'); 
%     waitforbuttonpress; 
% end

if ~pathFound
    if display
        imshow(map);
    end
    disp('no path found. maximum attempts reached');
    path = [];
    thetaPath = [];
    pathLength = inf; 
    return
end

% retrieve path from parent information
path = [];
thetaPath=[];
prev = I(1);
while prev > 0
    path = [RRTree(prev,1:2); path];
    thetaPath = [RRTree(prev,3); thetaPath];
    prev = RRTree(prev,4);
end
pathLength = 0;
for i=1:length(path)-1
    pathLength = pathLength + distanceCost(path(i,1:2),path(i+1,1:2),map); 
end % calculate path length
fprintf('Path Length=%d \n', pathLength); 
if display
    pause(0.1);
    imshow(map);
    rectangle('position',[1 1 size(map,2)-1 size(map,1)-1],'edgecolor','k');
    for i = 1:length(path)-1
        if abs(atan2(path(i+1,1)-path(i,1),path(i+1,2)-path(i,2)) - thetaPath(i+1))<1e-1
            pl = line(path(i:i+1,2),path(i:i+1,1));
            pl.Color = 'red';
            pl.LineStyle = '--';
        else
            pl = line([path(i,2); path(i,2)+stepSize * cos(thetaPath(i+1))],[path(i,1); path(i,1)+stepSize * sin(thetaPath(i+1))]);
            pl.Color = 'red';
            pl.LineStyle = '--';
            pl = line([path(i+1,2); path(i+1,2)-stepSize * cos(thetaPath(i+1))],[path(i+1,1); path(i+1,1)-stepSize * sin(thetaPath(i+1))]);
            pl.Color = 'red';
            pl.LineStyle = '--';
        end
    end
    pause(0.1);
%     disp('click/press any key'); 
%     waitforbuttonpress; 
end
end

RRT寻找路径的可视化如下。图中可以看到修改后的RRT可以穿过边界探索路径。

平面型二连杆机器人位形空间RRT避障轨迹规划（MATLAB）,平面,机器人,matlab

最后可以在位形空间中得到一条可行路径，并且由于多次选择，可以保证相对较优。如下图所示。

平面型二连杆机器人位形空间RRT避障轨迹规划（MATLAB）,平面,机器人,matlab

4. 可视化

这部分将利用RRT得到的避障轨迹可视化出来，绘出平面二连杆机器人的工作空间避障路线。

%% 机器人运动可视化
% 定义时间范围和时间步长
t = 1:1:size(robot_path,1);

% 初始化图形
figure;
xlabel('X轴');
ylabel('Y轴');
title('运动的平面二连杆机构和末端轨迹');

% 初始化末端轨迹数组
trajectory = zeros(length(t), 2);

for i = 1:length(t)   
    % 清除上一帧的图形，准备绘制下一帧
    clf;

    % 计算连杆角度（随时间变化）
    theta1 = robot_path(i,1);
    theta2 = robot_path(i,2);

    % 计算连杆末端坐标
    x1 = pos_robot_base(1) + link(1) * cos(theta1);
    y1 = pos_robot_base(2) + link(1) * sin(theta1);

    x2 = x1 + link(2) * cos(theta1 + theta2);
    y2 = y1 + link(2) * sin(theta1 + theta2);
    
    % 绘制连杆
    plot([pos_robot_base(1), x1], [pos_robot_base(2), y1], 'b', 'LineWidth', 2); % 绘制第一条连杆
    hold on;
    plot([x1, x2], [y1, y2], 'r', 'LineWidth', 2); % 绘制第二条连杆
    
    % 根据连杆长度调整显示区域
    axis([pos_robot_base(1)-sum(link) pos_robot_base(1)+sum(link) pos_robot_base(1)-sum(link) pos_robot_base(1)+sum(link)]);
    
    % 存储末端坐标到轨迹数组
    trajectory(i, :) = [x2, y2];

    % 绘制末端轨迹
    plot(trajectory(1:i, 1), trajectory(1:i, 2), 'g--', 'LineWidth', 2);
    
    % 绘制多边形障碍物
    for k = 1:length(pos_barrier_all)
        pos_barrier = cell2mat(pos_barrier_all(k));
        fill(pos_barrier(:, 1), pos_barrier(:, 2), 'b');
    end
    
    % 绘制底座、起始点与目标点
    pos_robot_init = forKine(link,pos_robot_base,theta_init);
    plot(pos_robot_base(1), pos_robot_base(2), 'ro', 'LineWidth', 2);
    plot(pos_robot_init(1), pos_robot_init(2), 'kx', 'LineWidth', 2);
    plot(pos_robot_goal(1), pos_robot_goal(2), 'bx', 'LineWidth', 2);

    % 暂停一段时间，产生动画效果
    pause(0.01);
end

最终得到平面型二连杆机器人运动轨迹如下。

平面型二连杆机器人位形空间RRT避障轨迹规划（MATLAB）,平面,机器人,matlab

总结

在构建位形空间图中，采样精度会大大影响程序运行时间，因此需要权衡采样精度的值。将机器人位形空间避障轨迹转换到工作空间时，由于位形空间的精度限制，会有精度损失，这会造成起点和终点位置不够精确，避障路径实际上可能经过障碍物等情况，可在绘制机器人位形空间图时略微外扩障碍物，也可减少采样位形空间图的步长。本代码较为简单，后续仍可以在求解效率，求解精度上进一步提升。

本人能力有限，在编写博客和代码的过程中难免会有错误，恳请批评指正，谢谢！文章来源地址https://www.toymoban.com/news/detail-839995.html

到了这里，关于平面型二连杆机器人位形空间RRT避障轨迹规划（MATLAB）的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！