并查集（详细解释+完整C语言代码）-Toy模板网

这篇具有很好参考价值的文章主要介绍了并查集（详细解释+完整C语言代码）。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

1概论

2.树的表现形式

3.代码实现

3.1创立集合

3.2合并

3.3查询

3.4路径压缩

第一个方法：查找时优化

第二个方法：合并时优化（加权标记法）

4.完整代码

4.1优化前

4.2优化后

1概论

并查集是一种十分精巧且实用的树形数据结构，它主要处理一些不相交集合的合并与查询问题。

不相交集合：即两集合交集为空。集合（1，2，3）与集合（4，5，6）不相交；

合并：将两不相交集合合并为一个集合。集合被合并为（1，2，3，4，5，6）

查询：查找此元素所处集合以及代表，可用于判断两元素是否同属一个集合

每个集合里有很多元素，我们选取其中一个元素作为此集合的代表。

我们不关心这个集合中具体包含了哪些元素；

我们不关心选哪个元素作为代表；

我们关心的是，给定一个元素，可以很快找到这个元素所在集合的代表；

我们关心的是，给定两个元素，判断他们是否处于同一个集合，如果不是，可以将两元素分别所处集合进行合并。

我们为什么关心这些，不关心那些呢？

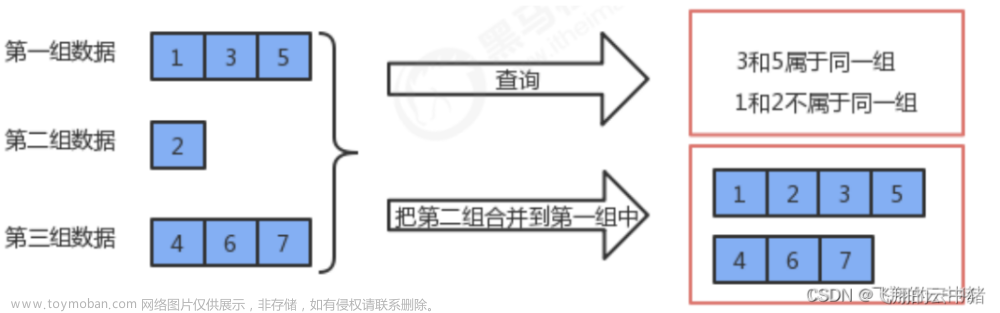
因为这就是并查集的精妙之处，它可以解决很多实际问题。比如下面两道题：

并查集代码,数据结构,数据结构,算法,c语言

我们以第二题为例，可以看出：只有两人之间（A与B）知道彼此是朋友，A不知道B与其他人的关系，B也不知道A与其他人的关系，甚至他们也不知道可能拥有共同的朋友C。题目假设朋友的朋友就是自己的朋友，相当于这群人是一伙的。现在，我想知道哪些人是一伙的。并查集就能轻松解决这个问题。

2.树的表现形式

并查集的实现原理也比较简单，就是用树来表示一个集合，树的每个结点就是集合的一个元素，根节点就是集合的代表。

并查集代码,数据结构,数据结构,算法,c语言

例如上图的两棵树，就对应的两个集合。我们继续用“朋友”的例子进行说明：刚才的朋友还知道彼此是朋友。而并查集实现时，就最多只知道自己的一个朋友，且不能是彼此知道。例如：D知道他的朋友是B，但B不知道D，只知道他的朋友是A。

以第一个集合为例：

D知道他的朋友为B，E知道他的朋友也为B，但D、E互相不认识；

B知道他的朋友为A，C知道他的朋友也为A，但B、C互相不认识，同时B也不知他还有朋友D、E；

A作为这个集合的代表，只知道自己，不知道他“下面”的朋友们。

尽管A~E是一伙的，他们却最多知道自己的一个朋友？那怎样才能让两人相见时，知道彼此是不是一伙的呢？

答案是：查询

除了代表（根节点），每个人都知道自己的一个朋友，那我们就可以让自己的朋友去问他的朋友，直到自己朋友的朋友...的朋友是这个集合的代表。由于代表（根节点）只有一个，而两人都知道自己和同一个代表是一伙的，那显然两人也是一伙的。这也就是查询的逻辑。

例1：D和C他们是一伙的吗？我们不知道，于是D问他的朋友B，B不是代表，B又去问他的朋友A，A是代表，好了，不用问了；C问他的朋友A，A是代表，不用问了。最终的代表都是A，显然，D和C是一伙的。

例2：E和H他们是一伙的吗？我们也不知道，于是E问他的朋友B，B不是代表，B又去问他的朋友A，A是代表，不用再问了；H问他的朋友G，G不是代表，G问他的朋友F，F是代表，不用再问了。显然，最后的代表不一样，他们不是一伙的。

现在又有个问题，E和H原本不是一伙的，但现在他们交朋友了，根据自己朋友的朋友都是朋友的逻辑，那显然上面两伙人就是一伙人了。这时，他们只要选择一个代表作为他们整体的代表就行了。这种情况叫什么呢？

答案是：合并（两集合合并为一个集合）

他们合并方式可以有很多种，比如让第二伙人的代表F与E交朋友（E作为F的父节点），也可以让F直接和第一伙的代表A交朋友（A作为F的父节点）。

并查集代码,数据结构,数据结构,算法,c语言

他们怎么交朋友，当然无所谓。但它作为数据结构，会影响到我们算法（特别是查询）的效率，所以怎么交朋友其实是有考究的。显然第二种就比第一种好。因为用第二种方法，H、G、F等找到所在集合代表的速度就更快。

在实现的过程中，我们就希望提高算法的效率，所以就需要路径压缩。

3.代码实现

在讲清楚逻辑后，我们就需要看看代码怎么实现了。并查集虽然是树形结构，但他只用数组就可以实现。

3.1创立集合

现在，假设使用一个足够长的数组来存储树结点，那么创立集合就是构造如下森林，其中每个元素都是一个单元素集合，即父节点为自身。

并查集代码,数据结构,数据结构,算法,c语言

void makeSet(int size)
{
	for (int i = 1; i <= size; i++)
	{
		//各自为各自的代表
		uset[i] = i;
	}
}

即:uset[1]=1,uset[2]=2,uset[3]=3,uset[4]=4,uset[5]=5,uset[6]=6。这意味着，uset[i]的朋友（父节点）是i自己。

3.2合并

例如，合并(1,2,3,4)，合并(5,6)，分别以1和5作为代表

并查集代码,数据结构,数据结构,算法,c语言

void unite(int x, int y) 
{
	//先找相对应的代表
	int x = find(x);
	int y = find(y);
	if (x == y)
	{
		return;
	}
	uset[x] = y;
}

合并2和1：分别找到自己的代表，都是自己2和1，显然2!=1，则uset[2]=1，这意味着，uset[2]的朋友是1；

合并3和2：分别找到自己的代表，都是自己3和2，显然3!=2，则uset[3]=2，这意味着3的朋友是2；

合并4和3：分别找到自己的代表，都是自己4和3，显然4!=3，则uset[4]=3，这意味着4的朋友是3；

这样（1，2，3，4）合并完成，此时可以发现它是一棵斜树。

同理，合并（5，6）就不再赘述。

现在，我们假设再合并（4,6）。

合并6和4：分别找到自己的代表5和1，显然5！=1，则uset[5]=1，这意味着5的朋友是3（1作为5的父节点）。

并查集代码,数据结构,数据结构,算法,c语言

当然，以上既可以是uset[x]=y，也可以是uset[y]=x。只要他们每次坚持一样的规则就行了，我们并不关注谁是父结点，谁是最后的根结点（代表）。

3.3查询

在上面的合并代码中，出现了find(x)，他其实就是查找x的代表是谁。

查询采用递归的思想，直到代表是自己（访问到根结点），否则就一直找朋友的朋友...find(uset[i])。

int find(int i)
{
	if (i == uset[i])
	{
		return i;
	}
	return find(uset[i]);
}

3.4路径压缩

在3.2中，如果采用此方法，最后就会成为一棵斜树。那么在查询时所耗费的时间就变多了，那有没有办法减少所用时间呢？

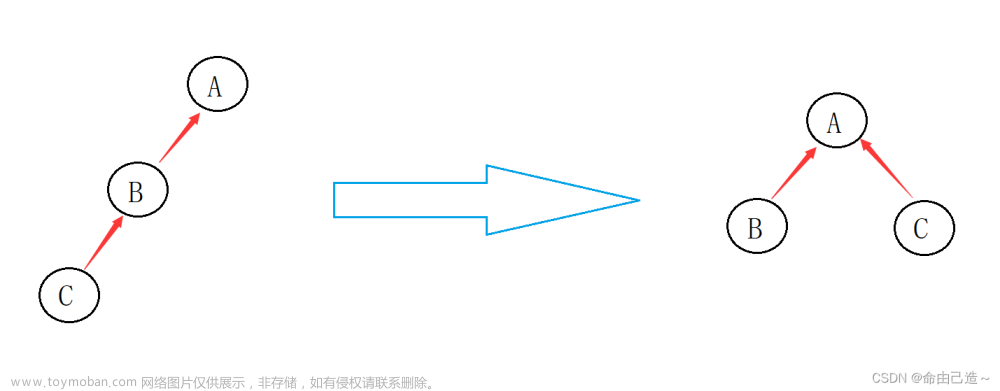
第一个方法：查找时优化

在每次查找时，令查找路径上的每个结点都指向根结点。

原先，4找代表1需要3次，现在只需要1次啦！

int find(int i)
{
	if (i == uset[i])
	{
		return i;
	}
	return uset[i] = find(uset[i]);//在第一次查找的时候 将结点直接连到跟
}

4找代表：代表不是自己，就一直找到根结点，并将根结点1作为4的父节点（直接朋友）

3找代表：代表不是自己，就一直找到根结点，并将根结点1作为3的父节点（直接朋友）

2找代表：代表是根结点了，不用改变

1找代表：代表是根结点了，不用改变

第二个方法：合并时优化（加权标记法）

我们回忆一下3.2中的合并，无论如何，我们都坚持着一个原则：uset[x]=y，即始终是前面那个数x作为孩子结点，后面那个数y作为x的父节点，最后合并成为了一棵斜树。

那如果我们加入一个判断呢？

如果x作为父节点更好，就让x当父亲，否则，就让y当父亲（结点）。

判断的依据是什么呢？

此时，我们要给每个结点加一个属性，俗称权值，即此结点的高度。

并查集代码,数据结构,数据结构,算法,c语言

例如合并x和y

若R[x]>R[y]，则uset[y]=x;

若R[x]<R[y]，则uset[x]=y;

若R[x]==R[y]，则都可以。

当合并1和5时，由于R[1]>R[5]，则uset[5]=1，让5的父节点为1。否则，就会让树的高度增加，查询效率就降低了。

根据以上信息可以得到：让权值更大的结点作父亲。

void unite(int x, int y)
{
	//先找相对应的代表
	int x = find(x);
	int y = find(y);
	if (x == y)
	{
		return;
	}
	//判断两棵树的高度 在决定谁为子树
	if (rank[x] < rank[y])
	{
		uset[x] = y;
	}
	else
	{
		uset[y] = x;

		if (rank[x] == rank[y])
		{
			rank[x]++;
		}
	}

当然，如果两结点权值相同，谁做父节点都可以，但此时，作父节点的那个结点权值就要增加1。

4.完整代码

这里只给出了模板，就没有写主函数啦。做题时只需套用模板即可。文章来源地址https://www.toymoban.com/news/detail-840377.html

4.1优化前

#include<stdio.h>
#include<stdlib.h>
#define MAXSIZE 100

int uset[MAXSIZE];//定义一个足够长的数组
//用下标来表示结点
/*
构造并查集
int size 有多少个节点
*/
void makeSet(int size)
{
	for (int i = 1; i < size; i++)
	{
		//各自为各自的代表
		uset[i] = i;
	}
}

/*
找到元素所在的集合的代表 如果位于同一集合 
*/
int find(int i)
{
	if (i == uset[i])
	{
		return i;
	}
	return find(uset[i]);
}

void unite(int x, int y) 
{
	//先找相对应的代表
	int x = find(x);
	int y = find(y);
	if (x == y)
	{
		return;
	}
	uset[x] = y;

}

4.2优化后

#include<stdio.h>
#include<stdlib.h>
#define MAXSIZE 100
/*
因为在特殊情况下 这棵树可能是一个长长的树链 设链的最后一个节点为x
每次执行find 相当于遍历整个链条
只需要把便利过的结点都改成跟的子节点 查询就会快很多
*/


int uset[MAXSIZE];//定义一个足够长的数组 每个结点
int rank[MAXSIZE];//树的高度

//用下标来表示结点
/*
构造并查集
int size 有多少个节点
*/
void makeSet(int size)
{
	for (int i = 1; i <= size; i++)
	{
		//各自为各自的代表
		uset[i] = i;
		//树的高度
		rank[i] = 0;
	}
}

/*
找到元素所在的集合的代表 如果位于同一集合
查找元素在哪个集合
*/
int find(int i)
{
	if (i == uset[i])
	{
		return i;
	}
	return uset[i] = find(uset[i]);//在第一次查找的时候 将结点直接连到跟
}

void unite(int x, int y)
{
	//先找相对应的代表
	int x = find(x);
	int y = find(y);
	if (x == y)
	{
		return;
	}
	//判断两棵树的高度 在决定谁为子树
	if (rank[x] < rank[y])
	{
		uset[x] = y;
	}
	else
	{
		uset[y] = x;

		if (rank[x] == rank[y])
		{
			rank[x]++;
		}
	}
}

到了这里，关于并查集（详细解释+完整C语言代码）的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！