leetcode69---x 的平方根-Toy模板网

这篇具有很好参考价值的文章主要介绍了leetcode69---x 的平方根。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

大家好，我是大唐，刚刷完了几道经典的leetcode题，今天给大家分享一道leetcode上面的二分查找经典题型---x 的平方根，我们往下看。

题目描述

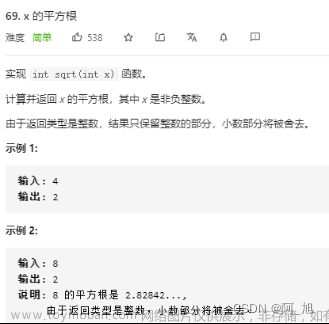
给你一个非负整数 x ，计算并返回 x 的 算术平方根 。

由于返回类型是整数，结果只保留 整数部分 ，小数部分将被 舍去。

注意：不允许使用任何内置指数函数和算符，例如 pow(x, 0.5) 或者 x ** 0.5 。

示例

leetcode69---x 的平方根,力扣高频刷题宝典,leetcode,算法,数据结构

求解方法

这道问题要求非负整数 x 的平方根。如果遇到平方根不是整数的情况呢？只取整数部分。例如，输入 x = 8，输出为 2。8 的平方根也就是 target 值，是小数 2.82842…。2 是小于 target 的元素中、最接近 target 的元素。

因此，这道问题实际是要查找 <= target 、且与 target 值最接近的元素。

可以用两种二分查找法来寻找：

方法一、标准二分查找法 while left <= right
这个方法应用标准二分查找法，只需改动 while 循环之后的语句 return -1为 return right。

为什么呢？我们来分析一下。当数组中没有值为 target 的元素时，因为 while 循环的条件是 left <= right，最后一次循环时搜寻区间有一个或两个元素，right = left 或 left +1。

对于本题要返回 < target、最接近 target 的元素索引的情况：

如果最后一次 while 循环时 middle > target，元素应该插入的位置是 middle - 1 ，而循环结束时 right = middle -1。

如果最后一次 while 循环时 middle < target，元素应该插入的位置是 middle。循环开始时只有 right = left = middle（如果 while 循环开始时 right = left + 1，而 middle < target，还会进入下一次循环，因此排除这种情况。），结束时 right = middle。

因此，只需把标准二分查找代码中 while 循环之后的语句由 return -1 改为 return right 即可。

代码如下：文章来源地址https://www.toymoban.com/news/detail-841299.html

class Solution:
    def mySqrt(self, x: int) -> int:
        # x = 0 或 1 时，直接返回结果
        if x <= 1:
            return x

        left, right = 1, x
        while left <= right:
            middle = left + (right - left) // 2
            if middle ** 2 == x:
                return middle
            elif middle ** 2 > x:
                right = middle - 1
            else:
                left = middle + 1
        
        return right

方法二、另一种二分查找法 while left < right
方法一，也就是标准二分查找法，是通过不断缩小搜索范围来查找某个元素。但是我们解决这一类型问题时发现，target 的取值可能是介于两个元素中间，虽然 middle 不等于 target，也许它就是最接近 target 取值的元素。比如本题例子求 8 的平方根，middle = 2 时。

对于本题要返回 < target、最接近 target 的元素索引的情况，当 middle < target 时，middle 位置有可能是我们要找的，下一次搜寻区间应该包含 middle。因此，此时 left = middle。

与方法一不同，这里的 while 循环条件为 left < right，因此循环终止时有 left = right，这样搜寻区间还有一个元素。这就是 <= target、最接近 target 的元素，最终返回它的索引（ left 或 right 都可以，两者相同)。

这里有一个小细节需要注意，因为 while 循环条件为 left < right，最后一次循环时搜寻区间有两个元素，当 left = right 时循环结束。但是我们求 middle 并不是精确的平均值，而是向下取整，这导致当搜寻区间只有两个元素时，middle 始终等于 left。这样，当 middle < target 时，left = middle，下一次循环 middle = (left + right) /2 = left ，没有更新搜寻区间，循环无法停止。怎么办呢？

代码如下：

class Solution:
    def mySqrt(self, x: int) -> int:
        # x=0或1时，直接返回结果
        if x <= 1:
            return x

        left, right = 1, x
        while left < right:
            middle = left + (right - left) // 2 + 1
            if middle ** 2 == x:
                return middle
            elif middle ** 2 > x:
                right = middle - 1
            else:
                left =  middle
                
        return left

到了这里，关于leetcode69---x 的平方根的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！