【第二十五课】动态规划：完全背包问题(acwing-3 / 公式推导 / 思路理解 / 优化 / c++代码)-Toy模板网

这篇具有很好参考价值的文章主要介绍了【第二十五课】动态规划：完全背包问题(acwing-3 / 公式推导 / 思路理解 / 优化 / c++代码)。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

思路

朴素代码

优化

公式推导上

二维代码

一维代码

公式理解上

在开始看完全背包问题之前，可能需要先了解01背包及其解决办法。指路👇

【第二十五课】动态规划：01背包问题(acwing-2 / 思路 / 含一维数组优化 / c++代码)

【第二十五课】动态规划：完全背包问题(acwing-3 / 公式推导 / 思路理解 / 优化 / c++代码),算法--学习笔记,动态规划,算法,c++

思路

这个问题和01背包的区别就是每件物品可以选无限次(当然在背包容量限制之内)。

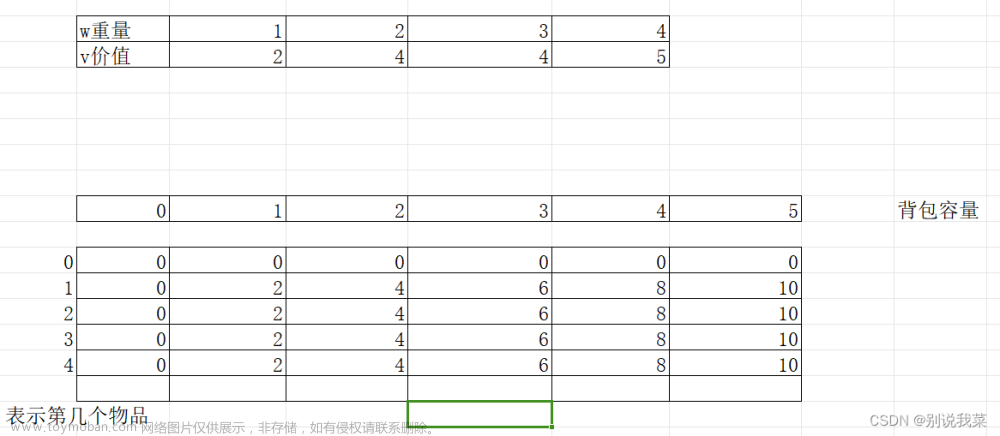
也就是说，01背包中我们在面对第i件物品的时候，有两种选择，分别是：选和不选，也就是第 i 件物品选择0次和1次，而完全背包也就是说，我们可选择的选项变多了，我们可以选择第i件物品 0，1，2，3，......k次，也就是在01背包分析问题方法的基础上，做了一点变化，如图

【第二十五课】动态规划：完全背包问题(acwing-3 / 公式推导 / 思路理解 / 优化 / c++代码),算法--学习笔记,动态规划,算法,c++

如果仅仅是这里发生了改变的话，其实我们在不考虑优化情况下，最朴素的写法应该是很容易得出的。

状态转移方程变为：dp[i][j]=max(dp[i-1][j],dp[i-1][j-k*v[i]]+k*w[i])

都是为了填充这个二维数组，只不过把选择从0和1两个变成了0-k个。

朴素代码

#include<iostream>
using namespace std;
const int N=1010;
int n,m;
int v[N],w[N];
int dp[N][N];
int main()
{
    cin>>n>>m;
    for(int i=1;i<=n;i++)cin>>v[i]>>w[i];
    for(int i=1;i<=n;i++)
    {
        for(int j=0;j<=m;j++)
        {
            for(int k=0;k*v[i]<=j;k++)
            {
                dp[i][j]=max(dp[i][j],dp[i-1][j-k*v[i]]+k*w[i]);
            }
        }
    }
    cout<<dp[n][m];
    return 0;
}

这种写法应该可以理解。

但是我们也看到了嵌套了三层循环。因此我们想着对他进行优化

优化

公式推导上

经过上面的分析我们知道完全与01背包问题的区别就是选择这件物品的次数，那么我们想试着用01背包的状态转移方程来写完全背包的，观察一下有没有什么规律，能够简化一层循环的。

下面图中是关于公式推导的过程

【第二十五课】动态规划：完全背包问题(acwing-3 / 公式推导 / 思路理解 / 优化 / c++代码),算法--学习笔记,动态规划,算法,c++

下面这个视频老师讲了具体的公式推导的过程，也对二维数组的填充过程给出了呈现，非常详细，推荐看一下帮助理解二维的写法。(可以倍速观看)

【叶老师讲信奥--完全背包问题】

下面这个老师是按照公式推导变化的方式进行讲解的，也很清晰，推荐看一下。

【完全背包问题求解-NOIP/CSP/蓝桥杯算法试学课-青少年C++编程】

二维代码

#include<iostream>
using namespace std;
const int N=1010;
int n,m;
int v[N],w[N];
int dp[N][N];
int main()
{
    cin>>n>>m;
    for(int i=1;i<=n;i++)cin>>v[i]>>w[i];
    for(int i=1;i<=n;i++)
    {
        for(int j=0;j<=m;j++)
        {
            dp[i][j]=dp[i-1][j];
            if(j>=v[i])dp[i][j]=max(dp[i][j],dp[i][j-v[i]]+w[i]);
        }
    }
    cout<<dp[n][m];
    return 0;
}

一维代码

#include<iostream>
using namespace std;
const int N=1010;
int n,m;
int v[N],w[N];
int dp[N];
int main()
{
    cin>>n>>m;
    for(int i=1;i<=n;i++)cin>>v[i]>>w[i];
    for(int i=1;i<=n;i++)
    {
        for(int j=v[i];j<=m;j++)
        {
            dp[j]=max(dp[j],dp[j-v[i]]+w[i]);
        }
    }
    cout<<dp[m];
    return 0;
}