【算法】LCA的三种算法-Toy模板网

这篇具有很好参考价值的文章主要介绍了【算法】LCA的三种算法。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

什么是LCA？

LCA(Least Common Ancestors),即最近公共祖先，是指在有根树中，找出某两个结点x和y最近的公共祖先。

三种算法

用三种算法可以求解LCA问题，分别为朴素算法、倍增算法和Tarjan算法。

朴素算法

倍增算法和Tarjan算法都在建立在朴素算法的思想下，因此，了解朴素算法的思想有助于更好的理解进阶算法。
朴素算法前置知识：邻接表，dfs。
假设我们要寻找某两个节点x和y的LCA，那么我们肯定是让深度更深的那个结点跳到另一个结点深度处，然后再让这两个结点一起向上跳，直到首次相遇。
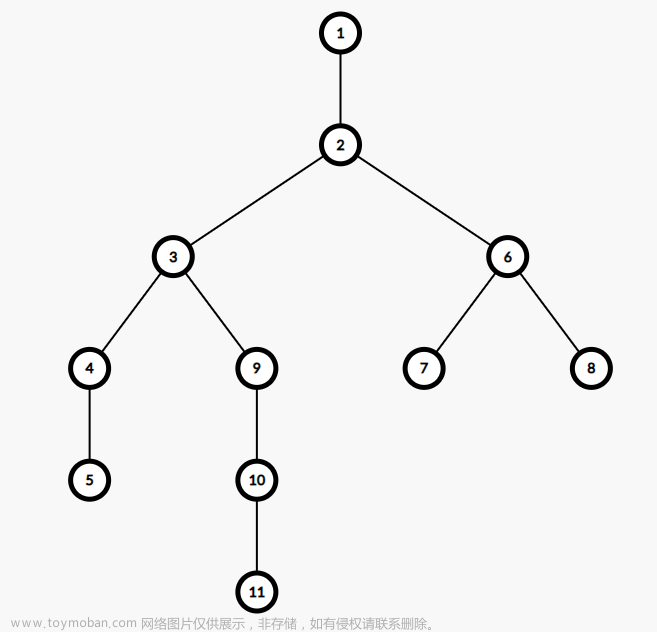
光说可以有些抽象，举个例子，就以下面这张图中的树为例。 lca算法,算法,深度优先
图中结点4先跳到结点3的位置，然后两个结点一起向上跳，随后跳到结点1处相遇，所以结点2和结点4的LCA为结点1。
也就是说，我们只要记录下每个结点的深度信息和祖先信息，就能通过逐个向上跳跃直至相遇来确定两个结点的LCA。
这便是LCA朴素算法的核心支撑所在，但是由于朴素算法每次跳跃一层，因此他的时间复杂度很差，尤其是当树退化为链的时候，那么如果我们让他跳跃多层，是不是可以更好更快的解决问题呢？答案是一定的，而接下来的倍增算法就是这个思想。

倍增算法

倍增算法前置知识：邻接表，DP&倍增，dfs。
倍增算法我们将会定义一个数组fa[i][j]表示结点i向上跳2^{j层所到的结点，从而实现了倍增跳跃，而且，通过有限的组合跳跃，我们到达任意结点处。例如向上5层，我们可以先向上跳跃2}2层之后，再向上跳跃2^0次方。同时，我们可以证明又fa[x][i] = fa[fa[x][i-1]][i-1],实质就是2^(i-1) + 2^(i-1) = 2^i.
同时，倍增LCA算法中还用到了贪心的思想，假如现在有两个结点x，y，假设x深度更大，则我们要尽可能地让x在不超过y的深度的前提下，尽可能地接近y，也就是跨的步子尽可能大！这样操作过后，结点x与结点y的深度就一定相同了。
相同之后，如果已经重合，直接return，如果没有，那么现在两个结点处于一个平行的位置。接下来我们让两个结点同时向上跳，也是能跳多大就跳多大，但是肯定是有限制的，就像上一步一样，这个限制就是只有在跳完之后他们结点不重合时才跳。这个地方有点绕，不要急，我们结合代码看一下。

点击查看代码

int lca(int u, int v) {
    if(depth[u] < depth[v]) swap(u, v);
    for(int i = MAXLOG - 1; i >= 0; i--) {
        if(depth[u] - (1 << i) >= depth[v]) {
            u = parent[u][i];
        }
    }
    if(u == v) return u;
// 注意看这里，这一步是平行之后的操作
    for(int i = MAXLOG - 1; i >= 0; i--) {
        if(parent[u][i] != parent[v][i]) {
            u = parent[u][i];
            v = parent[v][i];
        }
    }
    return parent[u][0];
}

我们注意到，在平行之后，只要在parent[u][i] != parent[v][i]的前提下尽可能地大跨步就能保证跳到最近的公共祖先的前一个位置，这个位置上面一层，也就是2^0方层就是公共祖先，同时也是最近的公共祖先。

Tarjan算法

Tarjan算法前置知识：邻接表，并查集，dfs。
Tarjan巧妙地将并查集和dfs结合在一起，实现了将单次查询地时间复杂度降到了常数级别的离线算法！
具体步骤如下：

对于每个节点u，初始化u的祖先为u本身，并标记u为已访问。
对于每条边(u,v)：
* 如果v未被访问，则对v进行深度优先搜索，并将v的祖先设置为u。
* 如果v已经被访问，那么u和v的最近公共祖先就是u的祖先和v的祖先的最小值。
在查询LCA问题时：
* 对于每个查询(q, u, v)，其中q为查询编号，u和v分别为查询的两个节点：
* 如果(u,v)已经被访问过，那么查询结果为(u,v)的最近公共祖先。
* 如果(u,v)未被访问过，那么查询结果为(u,v)的最近公共祖先的祖先。