【数据结构】五分钟自测主干知识（四）-Toy模板网

这篇具有很好参考价值的文章主要介绍了【数据结构】五分钟自测主干知识（四）。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

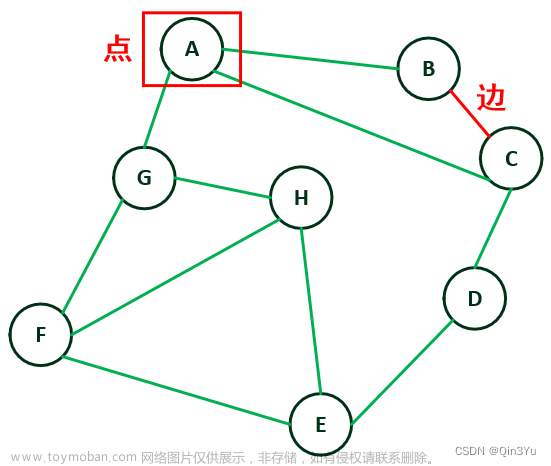
线性数据结构中有两个典型代表——栈和队列。它们的逻辑结构和线性表一致，不同之处在于其操作的特殊性：栈的插入和删除操作只能在线性表的一端进行，并且元素遵循“后进先出”的原则

今天我们先来讲述这个经典概念：“栈”

3.1栈的基本概念

栈（Stack）是一种线性结构，是一种限定只能在表的一端进行插入和删除操作的线性表。后进入栈的元素将最先出栈，因此栈又称LIFO（Last In First Out）表。

在栈中，允许插入和删除元素的一端被称为“栈顶”（Top），另一端则称为“栈底”（Bottom）。

栈的基本操作主要是插入（入栈）和删除（出栈）操作。（都是在栈顶完成）

下面给出栈的抽象数据类型定义：

ADT Stack{
数据对象:
数据关系:
基本操作：

InitStack(&S)
操作结果：创建一个空的栈S。

DestroyStack(&S)
操作结果：销毁栈S。
参数说明：栈S已存在。

ClearStack(&S)
操作结果：将栈S清空。
参数说明：栈S已存在。

StackEmpty(S)
操作结果：若栈S为空则返回TRUE；否则返回FALSE。
参数说明：栈S已存在。

StackLength(S)
操作结果：返回栈S中的元素个数，即栈的长度。
参数说明：栈S已存在。

GetTop(S,&e)
操作结果：将栈S的栈顶元素的值通过e返回。
参数说明：栈S已存在且非空。

Push(&S,e)
操作结果：将e插入为栈S新的栈顶元素。
参数说明：栈S已存在。

PoP(&S,&e)
操作结果：若栈非空，删除栈S的栈顶元素，并将其值赋给e。
参数说明：栈S已存在。

StackTraverse(S)
操作结果：从栈底到栈顶依次输出S中各个元素。
参数说明：栈S已存在。

}end ADT Stack

3.2栈的表示与实现

顺序栈

与顺序表类似，顺序栈也是利用顺序存储来实现栈的。即利用一组连续的存储单元依次存放自栈底到栈顶的元素。

顺序栈一般设置一个静态指针top来表示栈顶元素在顺序栈中的位置注意：这不是一个物理地址（内存指针），而是一个静态指针（即一个整型值），表示栈顶元素的数组下标。

一般用top=-1表示空栈

n个元素空间的顺序栈可以存储n个栈元素，满栈时top=n-1。

【数据结构】五分钟自测主干知识（四）,数据结构干货自测,数据结构

顺序栈表示如下：

typedef int ElemType;
#define STACK_INIT_SIZE 100
typedef struct {
	ElemType* elem;
	int stacksize;
	int top;
}SqStack;

下面来讲基本操作，因为都是在栈顶进行，这相对于线性表而言，都简单不少

1.顺序栈的初始化

需要给每个结构参数赋值

其中可以在msize参数中指定，也可以采用缺省值（用户未输入时的默认值STACK_INIT_SIZE)

void InitStack(SqStack& S, int msize = STACK_INIT_SIZE) {
	S.elem = new ElemType[msize];
	S.stacksize = msize;
	S.top = -1;
}

2.顺序栈的销毁

某些应用中如果栈贴别庞大，不使用了就应该及时销毁

void DestroyStack(SqStack& S) {
	delete[] S.elem;
	S.top = -1;
	S.stacksize = 0;
}

3.顺序栈获取栈顶元素

先看是不是空栈

bool GetTop(SqStack S, ElemType& e) {
	if (S.top == -1) {
		return false;
	}
	e = S.elem[S.top];
	return true;
}

4.入栈操作

将某元素插入到栈顶，作为新的栈顶元素，这称作“入栈”。

和顺序表一样，插入元素需要考虑顺序栈是否已经到达最大容量。

void Push(SqStack& S, ElemType e) {
	if (S.top == S.stacksize) {
		Increment(S);        //如果栈满则增加空间
	}
		S.elem[++S.top] = e;
}

Increment算法和顺序表的相似（见第二讲）

还是给大家展现一下吧，方便一下读者

void ErrorMsg(const char* a) {
	printf(a);        //错误处理函数，我们老熟人了，再打上去一次
}
void Increment(SqStack& S) {
	ElemType* a;
	a = new ElemType[S.stacksize + 1];//重新创建一个数组
	if (!a) { ErrorMsg("内存创建失败"); return; }
	for (int i = 0; i < S.stacksize; i++) {
		a[i] = S.elem[i];
	}
	delete[] S.elem;
	S.elem = a;
	S.stacksize++;//容量加一
}

5.出栈操作

若栈非空，将栈顶元素删除，原栈顶元素下一个元素成为新的栈顶元素。这称作“出栈”。

bool Pop(SqStack& S, ElemType& e) {
	if (S.top == -1) { return false; }
	e = S.elem[S.top--];
	return true;
}

顺序表初始化分配好最大的使用空间，如果在使用时出现栈满情况，就不得不重新分配一个更大块的连续空间，进行大批量的元素转移，因此尽量避免。

我来介绍下面的链栈，它具有比顺序栈更好的性能。

链栈

【数据结构】五分钟自测主干知识（四）,数据结构干货自测,数据结构

还记得我们之前（第三讲）定义了链表

typedef int ElemType;
typedef struct LNode{
    ElemType data;
    struct LNode* next;
}LNode, * LinkList;//LinkList就可以用来表示一个单链表

而我们的链栈的表示：

typedef LinkList LinkStack;

嘿嘿，完全一样（我就换个名字）

使用了一个LNode类型的指针来表示链栈，该指针指向链栈的栈顶。

基本操作如下：

1.链栈的初始化

void InitStack(LinkStack& S) {
	S = NULL;
}

2.链栈的销毁操作

不能仅仅简单地把栈顶指针置空，而是需要释放当前栈内所有元素的内存空间

（消除过期的对象引用，防止“内存泄漏”）

void DestroyStack(LinkStack& S) {
	while (S)
	{
		LNode* p = new LNode;
		p = S;
		S = S->next;//S指针后移
		delete p;
	}
}

3.链栈获取栈顶元素

bool GetTop(LinkStack& S, ElemType& e) {
	if (!S) return false;
	e = S->data;
	return true;
}

4.入栈操作

相当于单链表头插操作

void Push(LinkStack& S, ElemType e) {
	LNode* p = new LNode;
	p->data = e;
	p->next = S;
	S = p;
}

5.出栈操作

bool Pop(LinkStack& S, ElemType& e) {
	if (!S) return false;
	LNode* p = new LNode;
	p = S;
	S = S->next;	//S删除栈顶元素
	e = p->data;
	delete p;	//释放该结点内存空间
	return true;
}

可以看出，由于栈限制了插入和删除操作只能在栈顶，用链式存储实现栈正是发挥了链表的长处，避免了链表中前插和删除需要查询前驱元素的不足。

因此，和顺序存储比较，链式存储都是实现栈的更好选择。

为大家精心挑选有关栈的习题在我另一个附贴上，配合食用效果更佳~

【数据结构】经典习题自测（四）

接下来，我们将讲述栈的孪生兄弟：队列

附链接：【数据结构】五分钟自测主干知识（五）

方便大家自取自测~

文章来源地址https://www.toymoban.com/news/detail-841603.html

到了这里，关于【数据结构】五分钟自测主干知识（四）的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！