这篇具有很好参考价值的文章主要介绍了机器学习-线性代数。希望对大家有所帮助。如果存在错误或未考虑完全的地方,请大家不吝赐教,您也可以点击"举报违法"按钮提交疑问。
二维空间-Singular
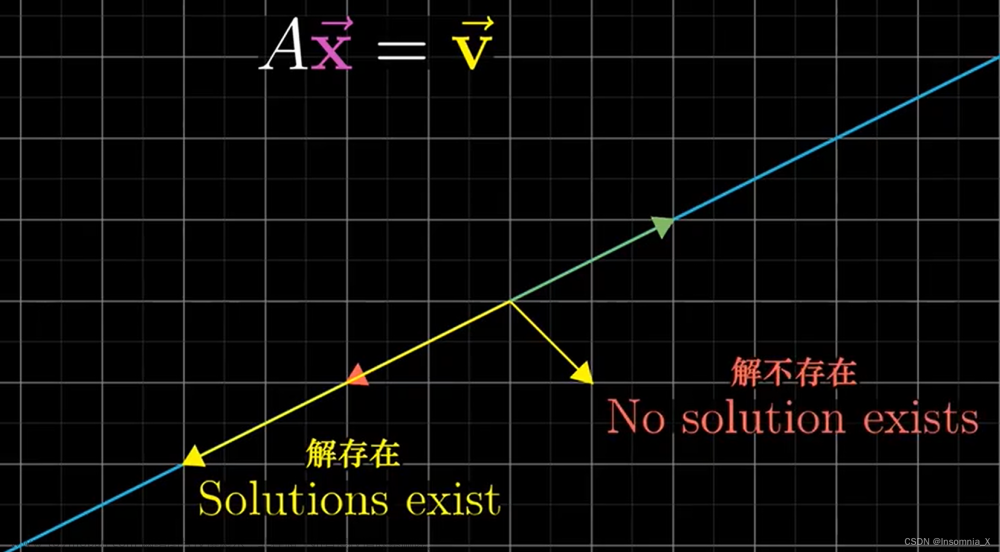
平行的线是linear dependence的,singular的,相交的线是Non-singular的,交点就是二元方程解
文章来源地址https://www.toymoban.com/news/detail-841723.html
在机器学习的计算过程中,等式右边的常数全部转化为0,确保每条线都经过(0,0)
文章来源:https://www.toymoban.com/news/detail-841723.html
三维空间-singular
平面相交于一条线或者重叠,则为singular
线性相关
有唯一解的方程组,是singular,所以不是linear dependence(线性相关)
可以通过部分方程推出其他方程,则相关
行列式
2*2矩阵,主对角线上的数字乘积-反对角线的数字乘积
行列式=0,则矩阵是singular
下半部为0的矩阵,行列式=对角的乘积,非零则non-singular
singular
解方程
行梯队
矩阵Rank(秩)
矩阵的行移动,不改变singular
矩阵的整行*数字,不改变,不改变singular
矩阵的非零行的数量 Rank of Matrix
the rank of martix if the information of this system
import numpy as np
# 定义矩阵A
A = np.array([[1, 2, 3], [4, 5, 6], [2, 1, 1]])
# 计算矩阵的秩
rank = np.linalg.matrix_rank(A)
print("矩阵A的秩为:", rank) # 输出:矩阵A的秩为: 3
图片压缩
原始图片的存储矩阵-Rank200,压缩后的Rank50
肉眼看不出区别,但存储空间降低75%
rank=矩阵行数,矩阵is non-singular,矩阵携带了最大的信息量,每行的信息都不相同
Rank=2-(Dimension of solution space)
dimension 解空间的维度
System1 只有一个点 解空间的维度=0
在更一般的情况下,如果有一个线性方程组包含 n 个未知数和 m 个方程,并且这个方程组有解,那么解空间的维度通常是 n - m(当然,这取决于方程组的具体形式,以及方程是否线性独立)。
矩阵变换成行梯形矩阵
对角线元素只有1没有0代表每行都有有效信息,矩阵non-singular
矩阵运算
vector 方向(direction)和大小(size,magnitude)
vector 矢量加法
每个维度的数字相加
矢量的距离
ab两个矢量的距离-三种表示方法
- a-b距离矢量的绝对值和
- a-b距离矢量的平方和的平方根
矢量的乘法
矢量的每个维度做乘法
点积-dotproduct
|u|向量的模长
<u,v>=|u|·|v|cos
矩阵向量运算
矩阵向量的线性变换
坐标系的映射
identity matrix 单位矩阵/恒等矩阵
inverse matrix 逆矩阵
取消上次矩阵变换的矩阵
神经网络
主成分分析PrincipalComponentAnalysis
降维算法
转换矩阵的行列式 determinant即转换后坐标系的单位面积
矩阵乘积的行列式 = 分别的行列式的乘积
det(AB)=det(A)·det(B)
矩阵的逆矩阵的行列式=矩阵的行列式的倒数
空间的基
任意两个不在一条直线上的向量都可以叫basis
在空间中的任意一点,可以通过向量的常数次组合到达
它们的组合叫span跨度
空间的跨度span
从远点经过span的向量能够到达坐标系的任意一点的最小的向量集叫basis
n维空间的basis的个数是n
特征基 eigenbasis
特征向量
特征值
线性无关
到了这里,关于机器学习-线性代数的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如若转载,请注明出处: 如若内容造成侵权/违法违规/事实不符,请点击违法举报进行投诉反馈,一经查实,立即删除!