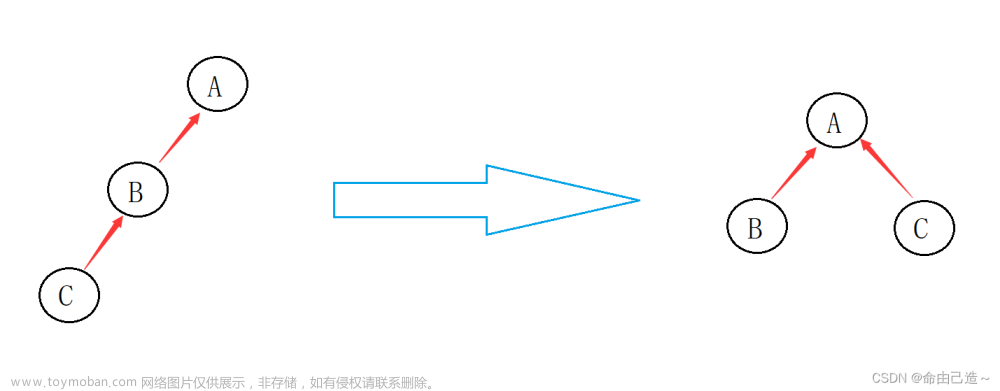
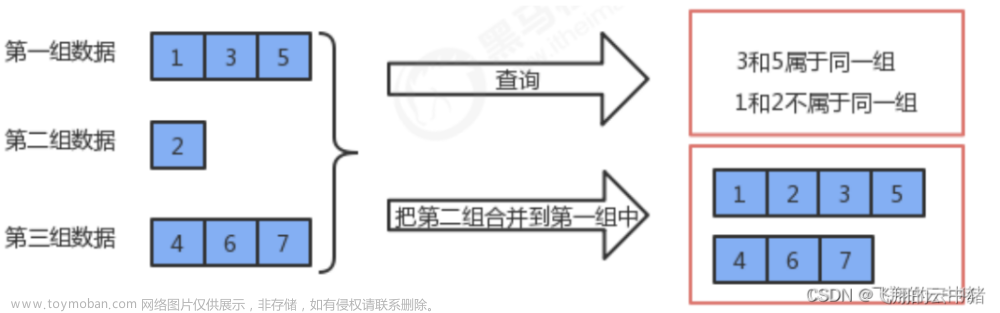
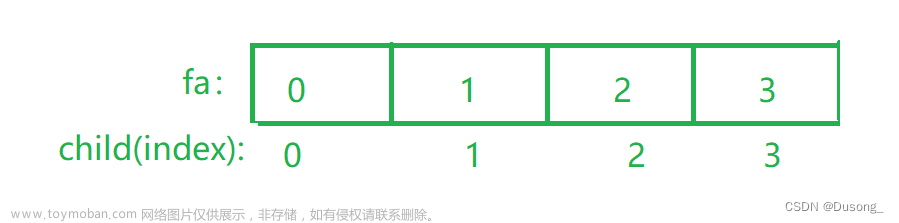
引言
今天写的题集是并查集,其实感觉有两个难点,一个是,要维护多余的信息和路径压缩,另一个难点则是抽象出来合并集合的这个操作,还是要不断地练习,看别人怎么去做,加油!
一、合并集合
标签:并查集
思路:模板题,没啥说的
题目描述:文章来源:https://www.toymoban.com/news/detail-842206.html
一共有 n 个数,编号是 1∼n,最开始每个数各自在一个集合中。
现在要进行 m 个操作,操作共有两种:
M a b,将编号为 a 和 b 的两个数所在的集合合并,如果两个数已经在同一个集合中,则忽略这个操作;
Q a b,询问编号为 a 和 b 的两个数是否在同一个集合中;
输入格式
第一行输入整数 n 和 m。
接下来 m 行,每行包含一个操作指令,指令为 M a b 或 Q a b 中的一种。
输出格式
对于每个询问指令 Q a b,都要输出一个结果,如果 a 和 b 在同一集合内,则输出 Yes,否则输出 No。
每个结果占一行。
数据范围
1≤n,m≤105
输入样例:
4 5
M 1 2
M 3 4
Q 1 2
Q 1 3
Q 3 4
输出样例:
Yes
No
Yes
示例代码:
#include <bits/stdc++.h>
using namespace std;
typedef long long LL;
typedef pair<int,int> PII;
#define x first
#define y second
const int N = 1e5+10;
int n, m;
int p[N];
int find(int x)
{
if(p[x] != x) p[x] = find(p[x]);
return p[x];
}
int main()
{
ios::sync_with_stdio(0); cin.tie(0); cout.tie(0);
cin >> n >> m;
for(int i = 1; i <= n; ++i) p[i] = i;
while(m--)
{
string op; cin >> op;
int a, b; cin >> a >> b;
int pa = find(a), pb = find(b);
if(op == "M")
{
if(pa != pb) p[pa] = pb;
}
else
{
if(pa == pb) puts("Yes");
else puts("No");
}
}
return 0;
}
二、连通块中点的数量
标签:并查集
思路:其实就是另外维护一个数量的信息,可以把一个连通块有多少个点的数量放到根结点中,然后找数量就查根结点的数量,然后连边就把结点信息更新到新的根结点就行了。
题目描述:
给定一个包含 n 个点(编号为 1∼n)的无向图,初始时图中没有边。
现在要进行 m 个操作,操作共有三种:
C a b,在点 a 和点 b 之间连一条边,a 和 b 可能相等;
Q1 a b,询问点 a 和点 b 是否在同一个连通块中,a 和 b 可能相等;
Q2 a,询问点 a 所在连通块中点的数量;
输入格式
第一行输入整数 n 和 m。
接下来 m 行,每行包含一个操作指令,指令为 C a b,Q1 a b 或 Q2 a 中的一种。
输出格式
对于每个询问指令 Q1 a b,如果 a 和 b 在同一个连通块中,则输出 Yes,否则输出 No。
对于每个询问指令 Q2 a,输出一个整数表示点 a 所在连通块中点的数量
每个结果占一行。
数据范围
1≤n,m≤105
输入样例:
5 5
C 1 2
Q1 1 2
Q2 1
C 2 5
Q2 5
输出样例:
Yes
2
3
示例代码:
#include <bits/stdc++.h>
using namespace std;
typedef long long LL;
typedef pair<int,int> PII;
#define x first
#define y second
const int N = 1e5+10;
int n, m;
int p[N], cnt[N];
int find(int x)
{
if(p[x] != x) p[x] = find(p[x]);
return p[x];
}
int main()
{
ios::sync_with_stdio(0); cin.tie(0); cout.tie(0);
cin >> n >> m;
for(int i = 1; i <= n; ++i) p[i] = i, cnt[i] = 1;
while(m--)
{
string op; cin >> op;
int a, b;
if(op == "C")
{
cin >> a >> b;
a = find(a), b = find(b);
if(a != b)
{
p[a] = p[b];
cnt[b] += cnt[a];
}
}
else if(op == "Q1")
{
cin >> a >> b;
a = find(a), b = find(b);
if(a != b) puts("No");
else puts("Yes");
}
else if(op == "Q2")
{
cin >> a;
a = find(a);
printf("%d\n", cnt[a]);
}
}
return 0;
}
三、网络分析
标签:并查集
思路1:这道题乍一眼可以直接拿
B
F
S
BFS
BFS 做,就是正常的连边, 然后搜索,只用开一个额外的数组用来记录每次遍历到的点就行了。
思路2:可以拿并查集来做,每个点的信息就是当前结点到根结点中的所有途径的点的信息,类似于差分的思想。每次如果在一个点中加上一个值,就相当于在根结点中加上一个值,如果两个连通块合并那么就是给原先的根结点减去现在根结点的值即可。
题目描述:
小明正在做一个网络实验。
他设置了 n 台电脑,称为节点,用于收发和存储数据。
初始时,所有节点都是独立的,不存在任何连接。
小明可以通过网线将两个节点连接起来,连接后两个节点就可以互相通信了。
两个节点如果存在网线连接,称为相邻。
小明有时会测试当时的网络,他会在某个节点发送一条信息,信息会发送到每个相邻的节点,之后这些节点又会转发到自己相邻
的节点,直到所有直接或间接相邻的节点都收到了信息。
所有发送和接收的节点都会将信息存储下来。
一条信息只存储一次。
给出小明连接和测试的过程,请计算出每个节点存储信息的大小。
输入格式
输入的第一行包含两个整数 n,m,分别表示节点数量和操作数量。
节点从 1 至 n 编号。
接下来 m 行,每行三个整数,表示一个操作。
如果操作为 1 a b,表示将节点 a 和节点 b 通过网线连接起来。当 a = b 时,表示连接了一个自环,对网络没有实质影响。
如果操作为 2 p t,表示在节点 p 上发送一条大小为 t 的信息。
输出格式
输出一行,包含 n 个整数,相邻整数之间用一个空格分割,依次表示进行完上述操作后节点 1 至节点 n 上存储信息的大小。
数据范围
1≤n≤10000,1≤m≤105,1≤t≤100
输入样例1:
4 8
1 1 2
2 1 10
2 3 5
1 4 1
2 2 2
1 1 2
1 2 4
2 2 1
输出样例1:
13 13 5 3
示例代码1: BFS 7/10
#include <bits/stdc++.h>
using namespace std;
typedef long long LL;
typedef pair<int,int> PII;
#define x first
#define y second
const int N = 1e4+10, M = 2 * N;
int n, m;
int h[N], e[M], ne[M], idx;
int dist[N];
bool st[N];
void add(int a, int b)
{
e[idx] = b, ne[idx] = h[a], h[a] = idx++;
}
void bfs(int S, int c)
{
memset(st, 0, sizeof st);
st[S] = true; dist[S] += c;
queue<int> q; q.push(S);
while(q.size())
{
int t = q.front(); q.pop();
for(int i = h[t]; i != -1; i = ne[i])
{
int j = e[i];
if(st[j]) continue;
st[j] = true; dist[j] += c;
q.push(j);
}
}
}
int main()
{
ios::sync_with_stdio(0); cin.tie(0); cout.tie(0);
memset(h, -1, sizeof h);
cin >> n >> m;
while(m--)
{
int op, a, b; cin >> op >> a >> b;
if(op == 1)
{
if(a == b) continue;
add(a,b), add(b,a);
}
else
{
bfs(a,b);
}
}
for(int i = 1; i <= n; ++i) cout << dist[i] << " ";
return 0;
}
示例代码2: 并查集
#include <bits/stdc++.h>
using namespace std;
typedef long long LL;
typedef pair<int,int> PII;
#define x first
#define y second
const int N = 1e4+10;
int n, m;
int p[N], d[N];
int find(int x)
{
if(x == p[x] || p[x] == p[p[x]]) return p[x];
int r = find(p[x]);
d[x] += d[p[x]];
p[x] = r;
return r;
}
int main()
{
ios::sync_with_stdio(0); cin.tie(0); cout.tie(0);
cin >> n >> m;
for(int i = 1; i <= n; ++i) p[i] = i;
while(m--)
{
int op, a, b; cin >> op >> a >> b;
int pa = find(a), pb = find(b);
if(op == 1)
{
if(pa == pb) continue;
d[pa] -= d[pb];
p[pa] = pb;
}
else
{
d[pa] += b;
}
}
for(int i = 1; i <= n; ++i)
{
if(i == find(i)) cout << d[i] << " ";
else cout << d[i] + d[find(i)] << " ";
}
return 0;
}
四、格子游戏
标签:并查集
思路:如果当前两个点时是赢了的话,那么这两个点之前已经在一个集合里了。那么我们就可以用这样的思路,然后可以将这个点集转换为一维的,就是跟数组一样所有行挪到一行。
题目描述:
Alice和Bob玩了一个古老的游戏:首先画一个 n×n 的点阵(下图 n=3 )。
接着,他们两个轮流在相邻的点之间画上红边和蓝边:
直到围成一个封闭的圈(面积不必为 1)为止,“封圈”的那个人就是赢家。因为棋盘实在是太大了,他们的游戏实在是太长了!
他们甚至在游戏中都不知道谁赢得了游戏。
于是请你写一个程序,帮助他们计算他们是否结束了游戏?
输入格式
输入数据第一行为两个整数 n 和 m。n表示点阵的大小,m 表示一共画了 m 条线。
以后 m 行,每行首先有两个数字 (x,y),代表了画线的起点坐标,接着用空格隔开一个字符,
假如字符是 D,则是向下连一条边,如果是 R 就是向右连一条边。
输入数据不会有重复的边且保证正确。
输出格式
输出一行:在第几步的时候结束。
假如 m 步之后也没有结束,则输出一行“draw”。
数据范围
1≤n≤200,1≤m≤24000
输入样例:
3 5
1 1 D
1 1 R
1 2 D
2 1 R
2 2 D
输出样例:
4
示例代码:文章来源地址https://www.toymoban.com/news/detail-842206.html
#include <bits/stdc++.h>
using namespace std;
typedef long long LL;
typedef pair<int,int> PII;
#define x first
#define y second
const int N = 40010;
int n, m;
int p[N];
int get(int x, int y)
{
return x * n + y;
}
int find(int x)
{
if(x != p[x]) p[x] = find(p[x]);
return p[x];
}
int main()
{
ios::sync_with_stdio(0); cin.tie(0); cout.tie(0);
int res = 0;
cin >> n >> m;
for(int i = 1; i <= n * n; ++i) p[i] = i;
for(int i = 1; i <= m; ++i)
{
int x, y; string op; cin >> x >> y >> op;
x--, y--;
int a = get(x,y), b;
if(op == "D")
{
b = get(x+1,y);
}
else
{
b = get(x,y+1);
}
a = find(a), b = find(b);
if(a == b)
{
res = i;
break;
}
p[a] = b;
}
if(!res) cout << "draw" << endl;
else cout << res << endl;
return 0;
}
到了这里,关于算法刷题day34:并查集的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!