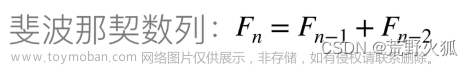【数据结构与算法】Kadane‘s算法（动态规划、最大子数组和）-Toy模板网

这篇具有很好参考价值的文章主要介绍了【数据结构与算法】Kadane‘s算法（动态规划、最大子数组和）。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

一、算法原理

Kadane's算法是一种用于解决最大子数组和问题的动态规划算法。这类问题的目标是在给定整数数组中找到一个连续的子数组，使其元素之和最大（数组含有负数）。

算法的核心思想是通过迭代数组的每个元素，维护两个变量来跟踪局部最优解和全局最优解。

以下是Kadane’s算法的详细步骤：

初始化：
- 令 maxEndingHere 表示在当前位置结束的最大子数组和，初始值为数组的第一个元素。
- 令 maxSoFar 表示全局最大子数组和，初始值也为数组的第一个元素。
迭代：
- 从数组的第二个元素开始迭代。
- 对于每个元素，计算在当前位置结束的最大子数组和：
  maxEndingHere = max(nums[i], maxEndingHere + nums[i]);
  这表示要么继续当前子数组，要么从当前位置开始一个新的子数组。
- 更新全局最大子数组和：
  maxSoFar = max(maxSoFar, maxEndingHere);
  如果在当前位置结束的子数组和大于全局最大和，更新全局最大和。
返回结果：
- 当迭代完成后，maxSoFar 中存储的即为最大子数组和。

复杂度：

时间复杂度：O(n)，其中 n 为 nums 数组的长度。我们只需要遍历一遍数组即可求得答案。
空间复杂度：O(1)。我们只需要常数空间存放若干变量。

图例：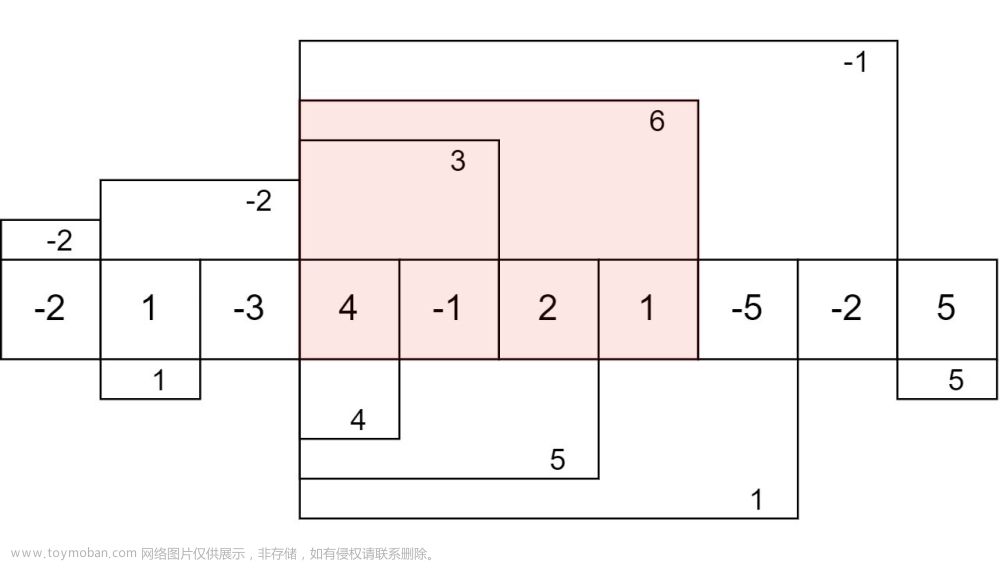
kadane's algorithm,Algorithm Notes,c语言,kadane,动态规划

简要说明：（如过当前值比前面的局部最大值+当前值还大，那么就从当前值开始继续计算局部最大值）

i=0,maxEndingHere 、maxSoFar 初始值都为数组第一个元素，-2；
开始循环，i=1，maxEndingHere = max(nums[1], maxEndingHere + nums[1])，即maxEndingHere = max(1, -2 + 1)=1，maxSoFar=1；
i=2， maxEndingHere = max(nums[2], maxEndingHere + nums[2])，即maxEndingHere = max(-3, 1 - 3)=-2，maxSoFar=1；
i=3，maxEndingHere = max(nums[3], maxEndingHere + nums[3])，即maxEndingHere = max(4, -2 + 4)=4，maxSoFar=4；
…

二、例题

2.1 最大子数组和

kadane's algorithm,Algorithm Notes,c语言,kadane,动态规划

解答：文章来源地址https://www.toymoban.com/news/detail-842411.html

int maxSubArray(int* nums, int numsSize) {
    int maxEndingHere  = nums[0], maxSoFar = nums[0];
    for (int i = 1; i < numsSize; i++) {
        maxEndingHere  = fmax(maxEndingHere  + nums[i], nums[i]);
        maxSoFar = fmax(maxSoFar, maxEndingHere );
    }
    return maxSoFar;
}

fmax是<math.h>中的函数，用于比较2个数字的大小，双精度。

简单换个写法：

int maxSubArray(int* nums, int numsSize) {
    int maxEndingHere  = nums[0], maxSoFar = nums[0];
    for (int i = 1; i < numsSize; i++) {
        maxEndingHere  = maxEndingHere  + nums[i]>nums[i]?maxEndingHere  + nums[i]:nums[i];
        maxSoFar = maxSoFar>maxEndingHere?maxSoFar:maxEndingHere;
    }
    return maxSoFar;
}

简单用三目表达式代替fmax函数。

2.2 环形子数组的最大和

kadane's algorithm,Algorithm Notes,c语言,kadane,动态规划

解答：

int maxSubarraySumCircular(int* nums, int numsSize) {
    if (nums == NULL || numsSize == 0) return 0;
    int maxSum = nums[0], minSum = nums[0];
    int maxCur = nums[0], minCur = nums[0];
    int sum = nums[0];

    for (int i = 1; i < numsSize; i++) {
        sum += nums[i];
        maxCur = fmax(nums[i], maxCur + nums[i]);
        minCur = fmin(nums[i], minCur + nums[i]);
        maxSum = fmax(maxSum, maxCur);
        minSum = fmin(minSum, minCur);
    }

    if (maxSum < 0) return maxSum; // 如果所有数都是负数，返回最大值
    return fmax(maxSum, sum - minSum); // 返回“不跨越头尾的最大子数组和”和“跨越头尾的最大子数组和”中的较大者
}