决策树的多类别分类-Toy模板网

这篇具有很好参考价值的文章主要介绍了决策树的多类别分类。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

1.背景介绍

决策树是一种常用的机器学习算法，它通过构建一棵树来对数据进行分类和预测。在这篇文章中，我们将深入探讨决策树在多类别分类任务中的应用，以及其核心概念、算法原理和实现细节。

决策树算法的主要优点包括易于理解、可视化、无需特征预处理等。然而，决策树也存在一些缺点，如过拟合、不稳定等。在实际应用中，我们需要结合其他算法和技术来提高决策树的性能。

2.核心概念与联系

决策树是一种基于树状结构的机器学习算法，它通过递归地划分特征空间来构建决策规则。在多类别分类任务中，决策树的目标是将输入数据分为多个类别，以便进行预测和分析。

决策树的核心概念包括：

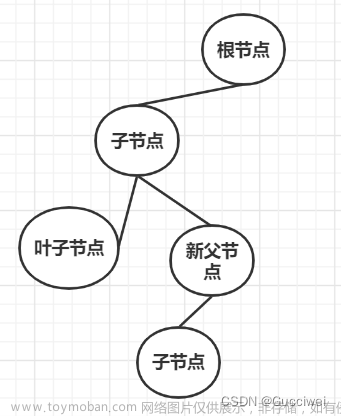
节点：决策树的每个结点表示一个特征，用于对输入数据进行划分。
分支：从结点出发的线段表示决策规则，用于将数据路由到不同的子结点。
叶子：决策树的每个叶子代表一个类别，用于对输入数据进行分类。

决策树与其他分类算法的关系包括：

逻辑回归：决策树是逻辑回归的一种特例，它通过构建树状结构来实现多类别分类。
支持向量机：决策树与支持向量机在处理非线性问题上有所不同，决策树通过递归地划分特征空间来实现非线性分类，而支持向量机通过核函数将数据映射到高维空间来实现线性分类。
神经网络：决策树与神经网络在结构上有所不同，决策树是树状结构，神经网络是有向有循环图状结构。然而，两者在处理多类别分类任务上具有相似的性能。

3.核心算法原理和具体操作步骤以及数学模型公式详细讲解

决策树的多类别分类算法原理如下：

从整个数据集中随机选择一个特征作为根结点。
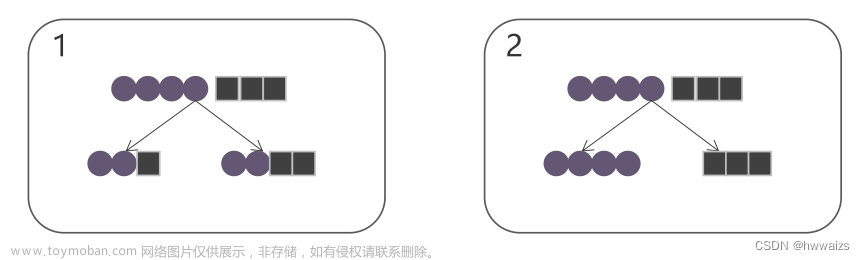
根据选定的特征将数据集划分为多个子集。
对每个子集递归地应用上述步骤，直到满足停止条件。
返回构建好的决策树。

决策树的构建过程可以通过ID3算法、C4.5算法等实现。这里我们以ID3算法为例，详细讲解其构建过程。

ID3算法的核心思想是：选择信息增益最高的特征作为分裂结点，直到满足停止条件。信息增益是衡量特征选择质量的指标，可以通过以下公式计算：

$$ IG(S, A) = \sum{a \in A} \frac{|Sa|}{|S|} IG(S_a, C) $$

其中，$S$ 是数据集，$A$ 是特征集合，$C$ 是类别集合，$IG(S, A)$ 是信息增益，$IG(S_a, C)$ 是条件信息增益。条件信息增益可以通过以下公式计算：

$$ IG(Sa, C) = -\sum{c \in C} \frac{|S{ac}|}{|S|} log2 \frac{|S_{ac}|}{|S|} $$

ID3算法的具体操作步骤如下：

从数据集中选择一个随机特征作为根结点。
计算所有可能的特征分裂结果的信息增益。
选择信息增益最高的特征作为分裂结点。
将数据集按照选定的特征划分，递归地应用上述步骤，直到满足停止条件。
返回构建好的决策树。

停止条件包括：

所有实例属于同一个类别。
所有特征已经被使用。
剩余实例数量达到阈值。

4.具体代码实例和详细解释说明

下面是一个使用Python实现ID3算法的代码示例：

```python import numpy as np from collections import Counter

class Node: def init(self, feature=None, threshold=None, left=None, right=None, class=None, impurity=None): self.feature = feature self.threshold = threshold self.left = left self.right = right self.class = class_ self.impurity = impurity

def entropy(y): hist = Counter(y) return -sum(p * log2(p) for p in hist.values())

def gini(y): hist = Counter(y) return 1 - sum((p / len(y)) ** 2 for p in hist.values())

def id3(X, Y, features): if len(np.unique(Y)) == 1: return Node(class=Y[0]) if len(features) == 0: return Node(impurity=gini(Y)) bestgain = -1 bestfeature = None for feature in features: gain = 0 for threshold in np.unique(X[:, feature]): leftidxs = X[:, feature] <= threshold rightidxs = ~leftidxs lefty, righty = Y[leftidxs], Y[rightidxs] leftx, rightx = X[leftidxs], X[rightidxs] leftimpurity = gini(lefty) if len(lefty) > 0 else 0 rightimpurity = gini(righty) if len(righty) > 0 else 0 gain = infogain(lefty, righty, leftimpurity, rightimpurity) if gain > bestgain: bestgain = gain bestfeature = feature features.remove(bestfeature) threshold = np.partition(X[:, bestfeature], -2)[-2] leftidxs = X[:, bestfeature] <= threshold rightidxs = ~leftidxs lefty, righty = Y[leftidxs], Y[rightidxs] leftx, rightx = X[leftidxs], X[rightidxs] return Node( feature=bestfeature, threshold=threshold, left=id3(leftx, lefty, features), right=id3(rightx, right_y, features) )

def info_gain(y1, y2, p1, p2): return entropy(np.concatenate((y1, y2))) - entropy(y1) - entropy(y2) ```

这个代码实现了ID3算法的核心逻辑，包括信息增益、信息熵、Gini索引等计算。通过递归地应用ID3算法，我们可以构建一个决策树，用于多类别分类任务。

5.未来发展趋势与挑战

随着数据规模的增加、计算能力的提升以及算法的发展，决策树在多类别分类任务中的应用将会继续发展。未来的挑战包括：

处理高维特征空间的挑战：随着数据的复杂性增加，决策树可能会 suffer from overfitting。为了解决这个问题，我们需要结合其他算法和技术，如随机森林、梯度提升树等。
解释性与可视化的挑战：尽管决策树具有很好的解释性，但在实际应用中，决策树的复杂性可能会影响其可视化和解释。我们需要开发更好的可视化工具和解释方法，以便更好地理解决策树的预测结果。
在线学习的挑战：随着数据流的增加，决策树在在线学习任务中的应用将会更加普遍。我们需要开发高效的在线决策树算法，以适应这种新的学习场景。