【图论】【深度优先搜索】【换根法】2858. 可以到达每一个节点的最少边反转次数-Toy模板网

这篇具有很好参考价值的文章主要介绍了【图论】【深度优先搜索】【换根法】2858. 可以到达每一个节点的最少边反转次数。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

本文涉及知识点

图论深度优先搜索有向图无向图树

LeetCode2858. 可以到达每一个节点的最少边反转次数

给你一个 n 个点的简单有向图（没有重复边的有向图），节点编号为 0 到 n - 1 。如果这些边是双向边，那么这个图形成一棵树。
给你一个整数 n 和一个二维整数数组 edges ，其中 edges[i] = [ui, vi] 表示从节点 ui 到节点 vi 有一条有向边。
边反转指的是将一条边的方向反转，也就是说一条从节点 ui 到节点 vi 的边会变为一条从节点 vi 到节点 ui 的边。
对于范围 [0, n - 1] 中的每一个节点 i ，你的任务是分别独立计算最少需要多少次边反转，从节点 i 出发经过一系列有向边，可以到达所有的节点。
请你返回一个长度为 n 的整数数组 answer ，其中 answer[i]表示从节点 i 出发，可以到达所有节点的最少边反转次数。
示例 1：
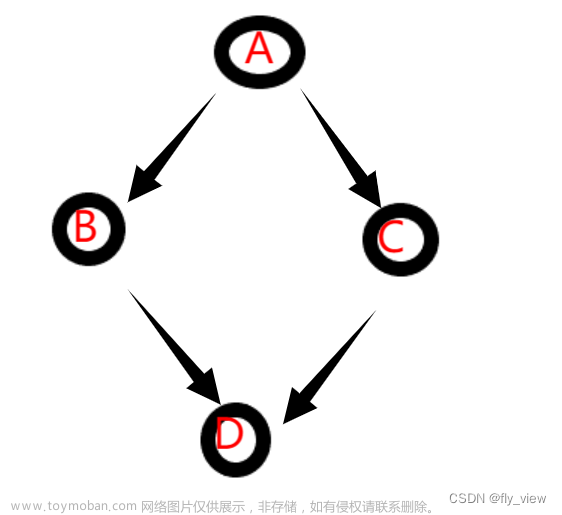
输入：n = 4, edges = [[2,0],[2,1],[1,3]]
输出：[1,1,0,2]
解释：上图表示了与输入对应的简单有向图。
对于节点 0 ：反转 [2,0] ，从节点 0 出发可以到达所有节点。
所以 answer[0] = 1 。
对于节点 1 ：反转 [2,1] ，从节点 1 出发可以到达所有节点。
所以 answer[1] = 1 。
对于节点 2 ：不需要反转就可以从节点 2 出发到达所有节点。
所以 answer[2] = 0 。
对于节点 3 ：反转 [1,3] 和 [2,1] ，从节点 3 出发可以到达所有节点。
所以 answer[3] = 2 。
示例 2：
输入：n = 3, edges = [[1,2],[2,0]]
输出：[2,0,1]
解释：上图表示了与输入对应的简单有向图。
对于节点 0 ：反转 [2,0] 和 [1,2] ，从节点 0 出发可以到达所有节点。
所以 answer[0] = 2 。
对于节点 1 ：不需要反转就可以从节点 2 出发到达所有节点。
所以 answer[1] = 0 。
对于节点 2 ：反转 [1,2] ，从节点 2 出发可以到达所有节点。
所以 answer[2] = 1 。
提示：
2 <= n <= 10⁵
edges.length == n - 1
edges[i].length == 2
0 <= ui == edges[i][0] < n
0 <= vi == edges[i][1] < n
ui != vi
输入保证如果边是双向边，可以得到一棵树。

深度优先搜索

如果这些边是双向边，那么这个图形成一棵树 $\rightarrow$ 无环。如果一棵树，所有的边，都由父节点指向子节点，则无需反转；有多少边反向，就需要翻转多少次。计算root的反向边的时间复杂度是O(n)。
性质一： root是树的根节点，child是它的子节点，将child转成根节点，除了 root 和 child 的父子互换外，其它父子关系不变。

大致流程

一，DFS 到各节点的父节点。
二，记录各节点和父节点组成的边，是指向父节点，还是反向。
三，DFS换根。

代码

把DFS中的bool转整形，直接改成整形，用时变成1/3。

class CNeiBo
{
public:	
	static vector<vector<int>> Two(int n, vector<vector<int>>& edges, bool bDirect, int iBase = 0) 
	{
		vector<vector<int>>  vNeiBo(n);
		for (const auto& v : edges)
		{
			vNeiBo[v[0] - iBase].emplace_back(v[1] - iBase);
			if (!bDirect)
			{
				vNeiBo[v[1] - iBase].emplace_back(v[0] - iBase);
			}
		}
		return vNeiBo;
	}	
	static vector<vector<std::pair<int, int>>> Three(int n, vector<vector<int>>& edges, bool bDirect, int iBase = 0)
	{
		vector<vector<std::pair<int, int>>> vNeiBo(n);
		for (const auto& v : edges)
		{
			vNeiBo[v[0] - iBase].emplace_back(v[1] - iBase, v[2]);
			if (!bDirect)
			{
				vNeiBo[v[1] - iBase].emplace_back(v[0] - iBase, v[2]);
			}
		}
		return vNeiBo;
	}
	static vector<vector<int>> Grid(int rCount, int cCount, std::function<bool(int, int)> funVilidCur, std::function<bool(int, int)> funVilidNext)
	{
		vector<vector<int>> vNeiBo(rCount * cCount);
		auto Move = [&](int preR, int preC, int r, int c)
		{
			if ((r < 0) || (r >= rCount))
			{
				return;
			}
			if ((c < 0) || (c >= cCount))

			{
				return;
			}
			if (funVilidCur(preR, preC) && funVilidNext(r, c))
			{
				vNeiBo[cCount * preR + preC].emplace_back(r * cCount + c);
			}
		};

		for (int r = 0; r < rCount; r++)
		{
			for (int c = 0; c < cCount; c++)
			{
				Move(r, c, r + 1, c);
				Move(r, c, r - 1, c);
				Move(r, c, r, c + 1);
				Move(r, c, r, c - 1);
			}
		}
		return vNeiBo;
	}
	static vector<vector<int>> Mat(vector<vector<int>>& neiBoMat)
	{
		vector<vector<int>> neiBo(neiBoMat.size());
		for (int i = 0; i < neiBoMat.size(); i++)
		{
			for (int j = i + 1; j < neiBoMat.size(); j++)
			{
				if (neiBoMat[i][j])
				{
					neiBo[i].emplace_back(j);
					neiBo[j].emplace_back(i);
				}
			}
		}
		return neiBo;
	}
};


class Solution {
public:
	vector<int> minEdgeReversals(int n, vector<vector<int>>& edges) {
		m_vToParent.resize(n);
		m_vToChild.resize(n);
		m_vAns.resize(n);
		m_vParent.assign(n, -2);

		auto vNeiBo = CNeiBo::Two(n, edges, false);
		DFS1(0, -1, vNeiBo);
		for (const auto& v : edges)
		{
			if (v[1] == m_vParent[v[0]])
			{
				m_vToParent[v[0]] = 1;//v[0]指向父亲的边存在
			}
			if (v[0] == m_vParent[v[1]])
			{
				m_vToChild[v[1]] = 1;//父亲指向v[0]的边存在
			}

		}
		m_vAns[0] = n - 1 - std::count(m_vToChild.begin(), m_vToChild.end(), 1);
		DFS2(0, -1, vNeiBo);
		return m_vAns;
	}
	void DFS1(int cur, int par, const vector<vector<int>>& vNeiBo)
	{
		m_vParent[cur] = par;
		for (const auto& next : vNeiBo[cur])
		{
			if (-2 != m_vParent[next])
			{
				continue;
			}
			DFS1(next, cur, vNeiBo);
		}
	}
	void DFS2(int cur, int par, const vector<vector<int>>& vNeiBo)
	{
		if (-1 != par)
		{
			m_vAns[cur] = m_vAns[par] - (1-m_vToChild[cur]) + (1-m_vToParent[cur]);
		}
		for (const auto& next : vNeiBo[cur])
		{
			if (m_vParent[next] != cur)
			{
				continue;
			}
			DFS2(next, cur, vNeiBo);
		}
	}

	vector<int> m_vAns;
	vector<int> m_vParent;
	vector<int> m_vToParent, m_vToChild;
};

代码二

力扣平台上： dfs中 m_vDirectNeiBo[par].count(i) 的用时是非DFS中的8倍。文章来源地址https://www.toymoban.com/news/detail-842598.html

class CNeiBo
{
public:	
	static vector<vector<int>> Two(int n, vector<vector<int>>& edges, bool bDirect, int iBase = 0) 
	{
		vector<vector<int>>  vNeiBo(n);
		for (const auto& v : edges)
		{
			vNeiBo[v[0] - iBase].emplace_back(v[1] - iBase);
			if (!bDirect)
			{
				vNeiBo[v[1] - iBase].emplace_back(v[0] - iBase);
			}
		}
		return vNeiBo;
	}	
	static vector<vector<std::pair<int, int>>> Three(int n, vector<vector<int>>& edges, bool bDirect, int iBase = 0)
	{
		vector<vector<std::pair<int, int>>> vNeiBo(n);
		for (const auto& v : edges)
		{
			vNeiBo[v[0] - iBase].emplace_back(v[1] - iBase, v[2]);
			if (!bDirect)
			{
				vNeiBo[v[1] - iBase].emplace_back(v[0] - iBase, v[2]);
			}
		}
		return vNeiBo;
	}
	static vector<vector<int>> Grid(int rCount, int cCount, std::function<bool(int, int)> funVilidCur, std::function<bool(int, int)> funVilidNext)
	{
		vector<vector<int>> vNeiBo(rCount * cCount);
		auto Move = [&](int preR, int preC, int r, int c)
		{
			if ((r < 0) || (r >= rCount))
			{
				return;
			}
			if ((c < 0) || (c >= cCount))

			{
				return;
			}
			if (funVilidCur(preR, preC) && funVilidNext(r, c))
			{
				vNeiBo[cCount * preR + preC].emplace_back(r * cCount + c);
			}
		};

		for (int r = 0; r < rCount; r++)
		{
			for (int c = 0; c < cCount; c++)
			{
				Move(r, c, r + 1, c);
				Move(r, c, r - 1, c);
				Move(r, c, r, c + 1);
				Move(r, c, r, c - 1);
			}
		}
		return vNeiBo;
	}
	static vector<vector<int>> Mat(vector<vector<int>>& neiBoMat)
	{
		vector<vector<int>> neiBo(neiBoMat.size());
		for (int i = 0; i < neiBoMat.size(); i++)
		{
			for (int j = i + 1; j < neiBoMat.size(); j++)
			{
				if (neiBoMat[i][j])
				{
					neiBo[i].emplace_back(j);
					neiBo[j].emplace_back(i);
				}
			}
		}
		return neiBo;
	}
};


class Solution {
public:
	vector<int> minEdgeReversals(int n, vector<vector<int>>& edges) {
		m_vDirectNeiBo.resize(n);
		m_vAns.resize(n);
		m_vParent.assign(n, -2);
		m_vLeve.resize(n);
		for (const auto& v : edges)
		{
			m_vDirectNeiBo[v[0]].emplace(v[1]);
		}
		auto vNeiBo = CNeiBo::Two(n, edges, false);
		int clock1 = clock();
		DFS(0, -1, vNeiBo);
		int clock2 = clock();		
		const int iMaxLeve = *std::max_element(m_vLeve.begin(),m_vLeve.end());
		vector<vector<int>> vLeves(iMaxLeve+1);		
		for (int i = 0; i < n; i++)
		{
			const int par = m_vParent[i];
			if ((-1 != par) && (!m_vDirectNeiBo[par].count(i)))
			{
				m_vAns[0]++;
			}
			vLeves[m_vLeve[i]].emplace_back(i);
		}
		for (const auto& v: vLeves)
		{
			for (const auto& cur : v)
			{
				const int par = m_vParent[cur];
				if (-1 == par)
				{
					continue;
				}
				m_vAns[cur] = m_vAns[par] - (!m_vDirectNeiBo[par].count(cur)) + (!m_vDirectNeiBo[cur].count(par));
			}
		}
		int clock3 = clock();
		std::cout << (clock2 - clock1) << " " << (clock3 - clock2);
		return m_vAns;
	}
	void DFS(int cur, int par, const vector<vector<int>>& vNeiBo)
	{	
		m_vParent[cur] = par;
		if (-1 != par)
		{
			m_vLeve[cur] = m_vLeve[par] + 1;
		}
		for (const auto& next : vNeiBo[cur])
		{
			if (-2 != m_vParent[next] )
			{
				continue;
			}
			DFS(next, cur, vNeiBo);
		}
	}
	vector<unordered_set<int>> m_vDirectNeiBo;
	vector<int> m_vAns,m_vParent,m_vLeve;
};