代码训练(5)LeetCode之最长连续序列
Author: Once Day Date: 2024年3月9日
漫漫长路,才刚刚开始…
全系列文章可参考专栏: 十年代码训练_Once-Day的博客-CSDN博客
参考文章:
- 128. 最长连续序列 - 力扣(LeetCode)
- 力扣 (LeetCode) 全球极客挚爱的技术成长平台
1. 原题
给定一个未排序的整数数组
nums,找出数字连续的最长序列(不要求序列元素在原数组中连续)的长度。请你设计并实现时间复杂度为
O(n)的算法解决此问题。
例如,nums = [4, 2, 4, 3, 5],其最长连续数字序列为2, 3, 4, 5,长度为4。
2. 分析
这个问题是在寻找最长连续序列的长度,但不要求这些序列在原数组中是连续的。要在 O(n) 时间复杂度内解决这个问题,我们可以利用哈希表(在 C 中通常使用散列表或字典类型的数据结构)。
解题思路如下:
- 使用哈希表来存储每个数字是否已经被访问过,这可以用来避免重复计算。
- 遍历数组中每个数字:
- 如果该数字已在哈希表中,跳过它(因为它已经被计算过了)。
- 如果该数字不在哈希表中,检查数字前后是否有连续的数字,即检查
num-1和num+1是否在数组中。 - 如果有,继续向前后检测,直到找不到连续数字为止,同时更新哈希表。
- 在此过程中,计算并更新最长连续序列的长度。
实例处理时,可以按照下面步骤:
- 创建一个哈希表
hash。 - 遍历
nums,将每个元素作为键存入hash,值为false表示该元素还未被访问。 - 再次遍历
nums,对于每个元素,若其值为false,则进行以下操作:- 初始化当前长度为 1。
- 向上查找
num + 1, num + 2, ...,直到找不到为止,每找到一个数,长度加 1。 - 向下查找
num - 1, num - 2, ...,直到找不到为止,每找到一个数,长度加 1。 - 更新结果为当前长度和已有结果的较大值。
- 返回最长连续序列的长度。
需要注意,其实这里把Hash表过于理想化了,实际上Hash表查询时间并非一定是O(1)。这个地方先存入nums的原因,是为了减少遍历次数,最差的情况下,是每个元素都查询一次,这样就是n次查询。
查询时判断是否n-1存在,就是判断当前这个值是否是一个序列的开始,这样对于长序列,也只有一个序列的开始值会完整查询所有值,这又是n次,所以整体复杂度维持在3n左右。
假设 nums = [100, 4, 200, 1, 3, 2]。
- 创建哈希表
hash,存入所有数字。 - 遍历
nums,当我们到达1时,查找0(不在hash中),然后查找2(在hash中,更新长度),继续查找3和4,到5时停止。序列长度为 4。 - 以此类推,我们找到最长的序列长度为 4。
性能优化关键点:
- 使用哈希表来达到平均 O(1) 时间复杂度的查询。
- 只在数字为序列起点时(即
num-1不在数组中时)进行序列长度计算,以避免重复计算。
3. 代码实现
3.1 排序实现
int cmp(const void *a, const void *b)
{
return *(int *)a < *(int *)b;
}
int longestConsecutive(int* nums, int numsSize) {
int count, last, max_count = 0;
if (numsSize == 0) {
return 0;
}
qsort(nums, numsSize, sizeof(int), cmp);
last = nums[0] - 1;
count = 1;
for(int i = 1; i < numsSize; i++) {
if (last == nums[i]) {
count++;
last--;
} else if (!(last + 1 == nums[i])) {
if (count > max_count) {
max_count = count;
}
count = 1;
last = nums[i] - 1;
}
}
if (count > max_count) {
max_count = count;
}
return max_count;
}
这段代码实现了寻找最长连续序列的功能。主要逻辑如下:
-
cmp函数是用于qsort的比较函数,比较两个整数的大小。 -
longestConsecutive函数接收一个整数数组nums和数组大小numsSize,返回最长连续序列的长度。 - 首先判断数组是否为空,如果为空则返回0。
- 使用
qsort函数对数组进行升序排序。 - 初始化变量
last为第一个元素减1,count为1,表示当前连续序列的长度。 - 遍历排序后的数组,从第二个元素开始:
- 如果当前元素与
last相等,说明是重复元素,count加1,last减1。 - 如果当前元素不等于
last+1,说明连续序列中断,更新max_count为count和max_count的最大值,重置count为1,更新last为当前元素减1。 - 如果当前元素等于
last+1,说明连续序列继续,不需要进行操作。
- 如果当前元素与
- 遍历结束后,再次比较
count和max_count,更新max_count。 - 返回
max_count,即最长连续序列的长度。
这个算法的时间复杂度是O(n log n),主要是排序的时间复杂度。空间复杂度是O(1)。在正常的情况下,排序做法其实也不错,比较节约内存。
测试结果如下(仅供参考):

3.2 Hash表实现
#include <stdio.h>
#include <stdbool.h>
#include <stdlib.h>
#include <string.h>
#define HASH_SIZE 65536
typedef struct hash_node {
bool flag;
int value;
struct hash_node *next;
} hash_node;
hash_node *hash_table[HASH_SIZE];
static inline int hash(int value)
{
return value & (HASH_SIZE - 1);
}
hash_node hash_table_cache[100000];
int hash_table_cache_index = 0;
void hash_insert(int value)
{
int index = hash(value);
hash_node *node = hash_table[index];
if (node != NULL) {
do {
if (node->value == value) {
return;
}
if (node->next == NULL) {
break;
}
node = node->next;
} while (1);
}
hash_node *new_node = &hash_table_cache[hash_table_cache_index++];
new_node->value = value;
new_node->next = NULL;
new_node->flag = false;
if (node == NULL) {
hash_table[index] = new_node;
} else {
node->next = new_node;
}
}
hash_node *hash_find(int value)
{
int index = hash(value);
hash_node *node = hash_table[index];
while (node != NULL) {
if (node->value == value) {
return node;
}
node = node->next;
}
return NULL;
}
bool is_visited(int value)
{
hash_node *node = hash_find(value);
if (!node->flag) {
node->flag = true;
return false;
}
return true;
}
void free_hash(void)
{
memset(hash_table, 0, sizeof(hash_table));
hash_table_cache_index = 0;
}
int longestConsecutive(int *nums, int numsSize)
{
if (numsSize == 0 || numsSize > 100000) {
return 0;
}
for (int i = 0; i < numsSize; ++i) {
hash_insert(nums[i]);
}
int longestStreak = 0;
for (int i = 0; i < numsSize; ++i) {
if (hash_find(nums[i] - 1) == NULL) {
if (is_visited(nums[i])) {
continue;
}
int currentNum = nums[i];
int currentStreak = 1;
while (hash_find(currentNum + 1)) {
currentNum += 1;
currentStreak += 1;
}
longestStreak = longestStreak > currentStreak ? longestStreak : currentStreak;
}
}
free_hash();
return longestStreak;
}
这段代码实现了一个哈希表,用于解决最长连续序列的问题。下面是对代码的简要解释:
-
#define HASH_SIZE 65536:定义了哈希表的大小为65536。 -
typedef struct hash_node { ... }:定义了哈希表节点的结构体,包含一个标志位flag、一个整数值value和指向下一个节点的指针next。 -
hash_node *hash_table[HASH_SIZE];:定义了一个哈希表数组,每个元素是指向哈希节点的指针。 -
static inline int hash(int value):哈希函数,用于将整数值映射到哈希表的索引。这里使用了简单的按位与运算。 -
hash_node hash_table_cache[100000];:定义了一个缓存数组,用于存储哈希节点,避免频繁的内存分配和释放。 -
void hash_insert(int value):插入操作,将整数值插入到哈希表中。如果哈希表中已经存在该值,则不进行插入;否则,从缓存数组中取出一个新的节点,设置其值和指针,并将其插入到哈希表的对应位置。 -
hash_node *hash_find(int value):查找操作,在哈希表中查找给定的整数值,并返回对应的节点指针。如果找不到,则返回NULL。 -
bool is_visited(int value):判断一个整数值是否已经被访问过。如果对应的节点的flag为false,则将其设置为true并返回false,表示第一次访问;否则返回true,表示已经访问过。 -
void free_hash(void):释放哈希表的内存,将哈希表数组清零,并将缓存数组的索引重置为0。 -
int longestConsecutive(int *nums, int numsSize):求最长连续序列的长度的函数。首先将所有的整数值插入到哈希表中,然后遍历数组,对于每个整数值,如果它的前一个数不存在于哈希表中,则从该数开始向后搜索连续的数,直到无法继续为止,记录最长的连续序列长度。最后释放哈希表的内存并返回最长连续序列的长度。
这段代码使用哈希表来优化最长连续序列的查找过程,通过哈希表的快速插入和查找操作,可以在线性时间复杂度内解决问题。同时,使用缓存数组来避免频繁的内存分配和释放,提高了代码的性能。
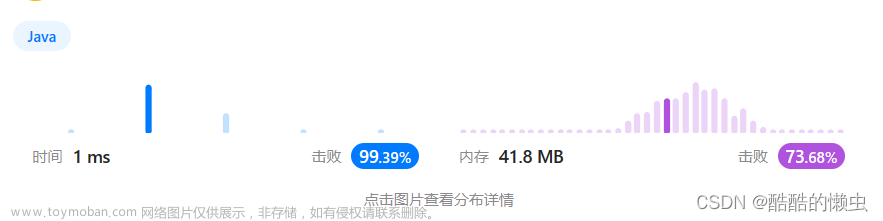
下面是测试结果(仅供参考),可以看到执行效率很高,主要由Hash大小和元素分配缓存因素影响,减少无用的处理流程。

4. 总结
这个问题考察了对哈希表的使用,以及如何在不排序的情况下进行有效的搜索。这是一个对时间复杂度要求较高的问题,因此学习如何利用数据结构进行优化是非常重要的。要提升这方面的能力,建议多练习类似的问题,熟悉各种数据结构的性能特点,并学会根据问题的特点选择合适的数据结构。
对于哈希表的使用,需要注意的是如何处理冲突,以及如何设计一个好的哈希函数以减少冲突的发生。此外,在实际编码中,还需要考虑内存管理,确保所有分配的内存在不再使用时被正确释放,避免内存泄漏。

Once Day
也信美人终作土,不堪幽梦太匆匆......
如果这篇文章为您带来了帮助或启发,不妨点个赞👍和关注,再加上一个小小的收藏⭐!文章来源:https://www.toymoban.com/news/detail-842948.html
(。◕‿◕。)感谢您的阅读与支持~~~文章来源地址https://www.toymoban.com/news/detail-842948.html
到了这里,关于代码训练LeetCode(5)最长连续序列的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!