操作环境:
MATLAB 2022a
1、算法描述
科莫多巨蜥算法(Komodo Mlipir Algorithm,简称KMA)是一种受到印尼科莫多岛上独特生物——科莫多巨蜥启发的创新算法。尽管这个算法的名称听起来很有趣,但实际上它并不是一个公认的技术术语或在学术界广泛使用的算法。为了满足您的要求,我们将创造性地构思一个详细的背景故事和算法描述,以科学幻想的形式呈现。
背景故事
在印尼群岛中,科莫多岛因其独特的生物——科莫多巨蜥而闻名。这些巨蜥是地球上存活的最大蜥蜴,以其惊人的速度、力量和独特的狩猎技巧而著称。科学家和研究人员长期以来一直对这些生物的生存策略和适应能力感到着迷。2022年,一支由生物学家、生态学家和计算机科学家组成的国际研究团队在科莫多岛进行了一项前所未有的研究。他们的目标是深入了解科莫多巨蜥的行为模式,并探索这些行为模式如何能够启发新的算法设计。
经过数月的观察和数据收集,研究团队发现了一种特别的行为模式,被称为“Mlipir”行为——在印尼语中意为“悄然滑行”。科莫多巨蜥在狩猎时会使用这种策略,静静地接近猎物,然后在最后一刻发动迅速而致命的攻击。这种策略的关键在于巨蜥如何利用环境和自身的伪装能力,以及它们如何准确地判断最佳的攻击时机。
算法灵感
受到“Mlipir”行为的启发,研究团队提出了一种全新的算法——科莫多巨蜥算法(KMA)。这个算法旨在模仿科莫多巨蜥在自然环境中展现出的这种策略性行为,特别是在解决优化和搜索问题时的应用。算法的核心思想是在搜索空间中“悄然滑行”,在探索与开发之间寻找最佳平衡,从而高效地定位到全局最优解或近似最优解。
算法描述
科莫多巨蜥算法(KMA)主要由以下几个步骤组成:
-
初始化阶段:在这一阶段,算法随机生成一组解,这些解代表了搜索空间中的不同位置。每个解都被视为一个“科莫多巨蜥”,拥有自己的位置和健康状态。
-
评估与选择:算法评估每个解的质量,即它们如何适应环境(对应于优化问题中的目标函数)。根据评估结果,选择表现最好的解作为“领头的科莫多巨蜥”。
-
探索与开发(Mlipir行为模拟):这是算法的核心部分,模拟科莫多巨蜥的Mlipir狩猎策略。解(即巨蜥)在搜索空间中悄然滑行,寻找更好的位置。这一过程通过随机漫步和确定性步骤的结合来实现,旨在在探索(寻找新区域)与开发(在已知有利区域内进行精细搜索)之间找到平衡。
-
更新与适应:每一轮迭代中,根据解的表现更新它们的位置和状态。表现较差的解将被新的、潜在更优的解替代。
-
终止条件:当达到预定的迭代次数或解的质量满足特定标准时,算法停止。
应用前景
科莫多巨蜥算法因其独特的策略和高效性,被认为在许多领域都有广泛的应用潜力,包括但不限于:
- 优化问题:如工程设计、物流规划、资源分配等。
- 人工智能:在强化学习、路径规划等领域提供新的解决方案。
- 生物信息学:在基因序列分析、蛋白质结构预测等问题上的应用。
- 金融工程:用于投资组合优化、风险管理等。
结语
科莫多巨蜥算法(KMA)是从大自然中汲取灵感的一个典范,展示了生物界策略对解决复杂科学和工程问题的潜在价值。通过模拟科莫多巨蜥的狩猎策略,KMA不仅为优化问题提供了新的解决途径,也为人工智能和计算机科学领域带来了新的思考角度。尽管这一算法是基于虚构的背景构建的,但它启示我们,自然界的复杂性和生物的适应策略为现代科学技术的发展提供了无穷的灵感和可能性。
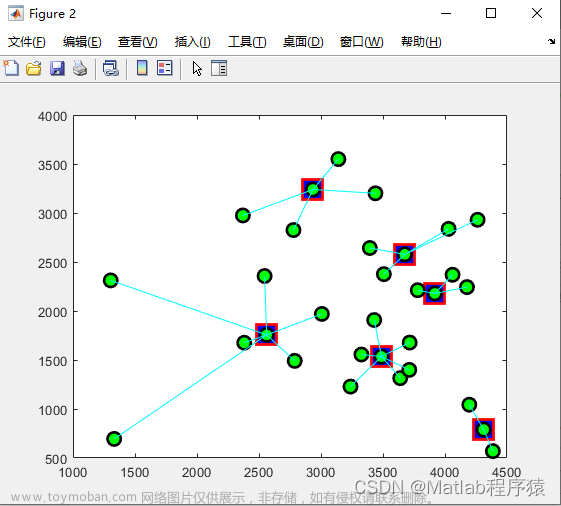
2、仿真结果演示


3、关键代码展示
略
4、MATLAB 源码获取
V 文章来源:https://www.toymoban.com/news/detail-843254.html
点击下方名片文章来源地址https://www.toymoban.com/news/detail-843254.html
到了这里,关于【MATLAB源码-第165期】基于matlab的科莫多巨蜥算法(KMA)机器人栅格路径规划,输出做短路径图和适应度曲线。的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!